摘要：最普遍的變換是線性變換，即和均將規范化應用于輸入的特征數據，而則另辟蹊徑，將規范化應用于線性變換函數的權重，這就是名稱的來源。他們不處理權重向量，也不處理特征數據向量，就改了一下線性變換的函數其中是和的夾角。

“ 深度神經網絡模型訓練之難眾所周知，其中一個重要的現象就是 Internal Covariate Shift. Batch Normalization 大法自 2015 年由Google 提出之后，就成為深度學習必備之神器。自 BN 之后， Layer Norm / Weight Norm / Cosine Norm 等也橫空出世。本文從 Normalization 的背景講起，用一個公式概括 Normalization 的基本思想與通用框架，將各大主流方法一一對號入座進行深入的對比分析，并從參數和數據的伸縮不變性的角度探討 Normalization 有效的深層原因。”

本文是該系列的第二篇。

03、主流 Normalization 方法梳理

在上一節中，我們提煉了 Normalization 的通用公式：

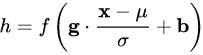
對照于這一公式，我們來梳理主流的四種規范化方法。

3.1 ?Batch Normalization —— 縱向規范化

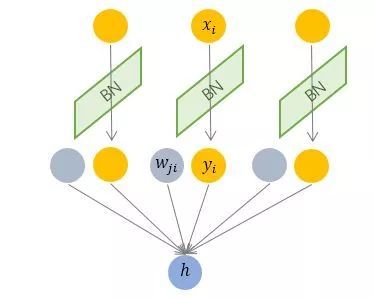
Batch Normalization 于2015年由 Google 提出，開 Normalization 之先河。其規范化針對單個神經元進行，利用網絡訓練時一個 mini-batch 的數據來計算該神經元 x_i 的均值和方差,因而稱為 Batch Normalization。

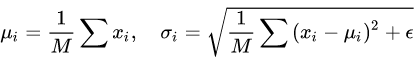
其中 M 是 mini-batch 的大小。

按上圖所示，相對于一層神經元的水平排列，BN 可以看做一種縱向的規范化。由于 BN 是針對單個維度定義的，因此標準公式中的計算均為 element-wise 的。

BN 獨立地規范化每一個輸入維度 x_i ，但規范化的參數是一個 mini-batch 的一階統計量和二階統計量。這就要求 每一個 mini-batch 的統計量是整體統計量的近似估計，或者說每一個 mini-batch 彼此之間，以及和整體數據，都應該是近似同分布的。分布差距較小的 mini-batch 可以看做是為規范化操作和模型訓練引入了噪聲，可以增加模型的魯棒性；但如果每個 mini-batch的原始分布差別很大，那么不同 mini-batch 的數據將會進行不一樣的數據變換，這就增加了模型訓練的難度。

因此，BN 比較適用的場景是：每個 mini-batch 比較大，數據分布比較接近。在進行訓練之前，要做好充分的 shuffle. 否則效果會差很多。

另外，由于 BN 需要在運行過程中統計每個 mini-batch 的一階統計量和二階統計量，因此不適用于 動態的網絡結構 和 RNN 網絡。不過，也有研究者專門提出了適用于 RNN 的 BN 使用方法，這里先不展開了。

3.2 Layer Normalization —— 橫向規范化

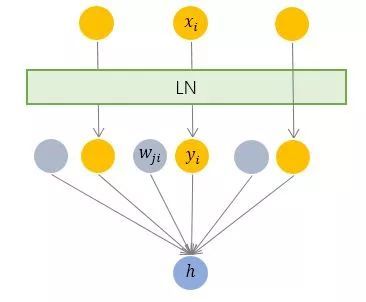
層規范化就是針對 BN 的上述不足而提出的。與 BN 不同，LN 是一種橫向的規范化，如圖所示。它綜合考慮一層所有維度的輸入，計算該層的平均輸入值和輸入方差，然后用同一個規范化操作來轉換各個維度的輸入。

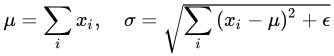
其中 i 枚舉了該層所有的輸入神經元。對應到標準公式中，四大參數 μ, σ , b, g均為標量（BN中是向量），所有輸入共享一個規范化變換。

LN 針對單個訓練樣本進行，不依賴于其他數據，因此可以避免 BN 中受 mini-batch 數據分布影響的問題，可以用于 小mini-batch場景、動態網絡場景和 RNN，特別是自然語言處理領域。此外，LN 不需要保存 mini-batch 的均值和方差，節省了額外的存儲空間。

但是，BN 的轉換是針對單個神經元可訓練的——不同神經元的輸入經過再平移和再縮放后分布在不同的區間，而 LN 對于一整層的神經元訓練得到同一個轉換——所有的輸入都在同一個區間范圍內。如果不同輸入特征不屬于相似的類別（比如顏色和大小），那么 LN 的處理可能會降低模型的表達能力。

3.3 Weight Normalization —— 參數規范化

前面我們講的模型框架

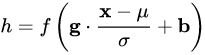
中，經過規范化之后的 y 作為輸入送到下一個神經元，應用以 w 為參數的f_w() 函數定義的變換。最普遍的變換是線性變換，即?

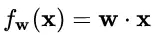
BN 和 LN 均將規范化應用于輸入的特征數據 x ，而 WN 則另辟蹊徑，將規范化應用于線性變換函數的權重 w ，這就是 WN 名稱的來源。

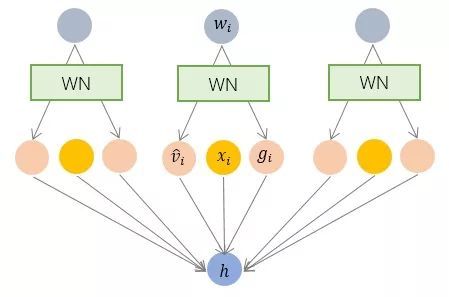
具體而言，WN 提出的方案是，將權重向量 w 分解為向量方向 v 和向量模 g 兩部分：

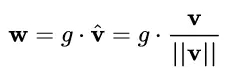
其中 v 是與 g 同維度的向量， ||v||是歐式范數，因此 v / ||v|| 是單位向量，決定了 w 的方向；g 是標量，決定了 w 的長度。由于 ||w|| = |g| ，因此這一權重分解的方式將權重向量的歐氏范數進行了固定，從而實現了正則化的效果。

乍一看，這一方法似乎脫離了我們前文所講的通用框架？

并沒有。其實從最終實現的效果來看，異曲同工。我們來推導一下看。?

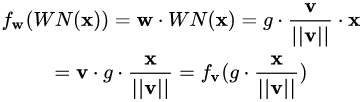
對照一下前述框架：

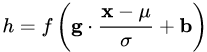
我們只需令：

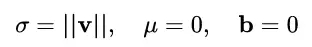
就完美地對號入座了！

回憶一下，BN 和 LN 是用輸入的特征數據的方差對輸入數據進行 scale，而 WN 則是用 神經元的權重的歐氏范式對輸入數據進行 scale。雖然在原始方法中分別進行的是特征數據規范化和參數的規范化，但本質上都實現了對數據的規范化，只是用于 scale 的參數來源不同。

另外，我們看到這里的規范化只是對數據進行了 scale，而沒有進行 shift，因為我們簡單地令 μ = 0. 但事實上，這里留下了與 BN 或者 LN 相結合的余地——那就是利用 BN 或者 LN 的方法來計算輸入數據的均值 μ。

WN 的規范化不直接使用輸入數據的統計量，因此避免了 BN 過于依賴 mini-batch 的不足，以及 LN 每層轉換器的限制，同時也可以用于動態網絡結構。

3.4 Cosine Normalization —— 余弦規范化

Normalization 還能怎么做？

我們再來看看神經元的經典變換?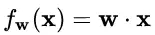

對輸入數據 x 的變換已經做過了，橫著來是 LN，縱著來是 BN。

對模型參數 w 的變換也已經做過了，就是 WN。

好像沒啥可做的了。

然而天才的研究員們盯上了中間的那個點，對，就是 ·

他們說，我們要對數據進行規范化的原因，是數據經過神經網絡的計算之后可能會變得很大，導致數據分布的方差爆炸，而這一問題的根源就是我們的計算方式——點積，權重向量 w 和 特征數據向量 x 的點積。向量點積是無界（unbounded）的啊！

那怎么辦呢？我們知道向量點積是衡量兩個向量相似度的方法之一。哪還有沒有其他的相似度衡量方法呢？有啊，很多啊！夾角余弦就是其中之一啊！而且關鍵的是，夾角余弦是有確定界的啊，[-1, 1] 的取值范圍，多么的美好！仿佛看到了新的世界！

于是，Cosine Normalization 就出世了。他們不處理權重向量 w ，也不處理特征數據向量 x ，就改了一下線性變換的函數：

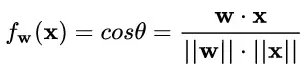
其中 θ 是 w 和 x 的夾角。然后就沒有然后了，所有的數據就都是 [-1, 1] 區間范圍之內的了！

不過，回過頭來看，CN 與 WN 還是很相似的。我們看到上式中，分子還是 w 和 x 的內積，而分母則可以看做用 w 和 x 二者的模之積進行規范化。對比一下 WN 的公式：

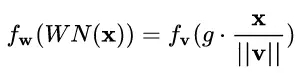
一定程度上可以理解為，WN 用 權重的模 ||v|| 對輸入向量進行 scale，而 CN 在此基礎上用輸入向量的模 ||x|| 對輸入向量進行了進一步的 scale.

CN 通過用余弦計算代替內積計算實現了規范化，但成也蕭何敗蕭何。原始的內積計算，其幾何意義是 輸入向量在權重向量上的投影，既包含 二者的夾角信息，也包含 兩個向量的scale信息。去掉scale信息，可能導致表達能力的下降，因此也引起了一些爭議和討論。具體效果如何，可能需要在特定的場景下深入實驗。

現在，BN, LN, WN 和 CN 之間的來龍去脈是不是清楚多了？

04、Normalization 為什么會有效

我們以下面這個簡化的神經網絡為例來分析。

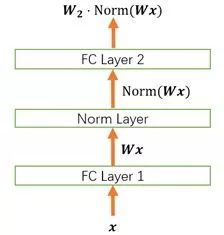
4.1 Normalization 的權重伸縮不變性

權重伸縮不變性（weight scale invariance）指的是，當權重 W 按照常量 λ 進行伸縮時，得到的規范化后的值保持不變，即：

其中 W" = λW 。

上述規范化方法均有這一性質，這是因為，當權重 ?W 伸縮時，對應的均值和標準差均等比例伸縮，分子分母相抵。

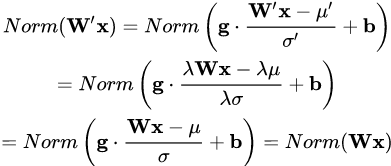
權重伸縮不變性可以有效地提高反向傳播的效率。由于

因此，權重的伸縮變化不會影響反向梯度的 Jacobian 矩陣，因此也就對反向傳播沒有影響，避免了反向傳播時因為權重過大或過小導致的梯度消失或梯度爆炸問題，從而加速了神經網絡的訓練。

權重伸縮不變性還具有參數正則化的效果，可以使用更高的學習率。由于

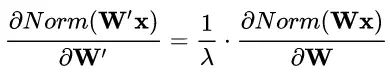
因此，下層的權重值越大，其梯度就越小。這樣，參數的變化就越穩定，相當于實現了參數正則化的效果，避免參數的大幅震蕩，提高網絡的泛化性能。進而可以使用更高的學習率，提高學習速度。

4.2 Normalization 的數據伸縮不變性

數據伸縮不變性（data scale invariance）指的是，當數據 x 按照常量 λ 進行伸縮時，得到的規范化后的值保持不變，即：

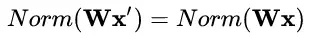
其中 x" = λx 。

數據伸縮不變性僅對 BN、LN 和 CN 成立。因為這三者對輸入數據進行規范化，因此當數據進行常量伸縮時，其均值和方差都會相應變化，分子分母互相抵消。而 WN 不具有這一性質。

數據伸縮不變性可以有效地減少梯度彌散，簡化對學習率的選擇。

對于某一層神經元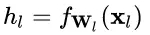而言，展開可得

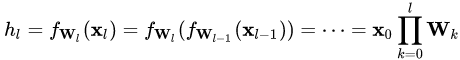
每一層神經元的輸出依賴于底下各層的計算結果。如果沒有正則化，當下層輸入發生伸縮變化時，經過層層傳遞，可能會導致數據發生劇烈的膨脹或者彌散，從而也導致了反向計算時的梯度爆炸或梯度彌散。

加入 Normalization 之后，不論底層的數據如何變化，對于某一層神經元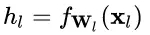?而言，其輸入 x_l 永遠保持標準的分布，這就使得高層的訓練更加簡單。從梯度的計算公式來看：

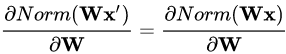
數據的伸縮變化也不會影響到對該層的權重參數更新，使得訓練過程更加魯棒，簡化了對學習率的選擇。

[1] Sergey Ioffe and Christian Szegedy. Accelerating Deep Network Training by Reducing Internal Covariate Shift.（https://arxiv.org/abs/1502.03167 ）

[2] Jimmy L. Ba, Jamie R. Kiros, Geoffrey E. Hinton. [1607.06450] Layer Normalization.（https://arxiv.org/abs/1607.06450 ）

[3] Tim Salimans, Diederik P. Kingma. A Simple Reparameterization to Accelerate Training of Deep Neural Networks.（https://arxiv.org/abs/1602.07868 ）

[4] Chunjie Luo, Jianfeng Zhan, Lei Wang, Qiang Yang. Using Cosine Similarity Instead of Dot Product in Neural Networks.（https://arxiv.org/abs/1702.05870 ）

[5] Ian Goodfellow, Yoshua Bengio, Aaron Courville. Deep Learning.（http://www.deeplearningbook.org/ ）歡迎加入本站公開興趣群

商業智能與數據分析群

興趣范圍包括各種讓數據產生價值的辦法，實際應用案例分享與討論，分析工具，ETL工具，數據倉庫，數據挖掘工具，報表系統等全方位知識

QQ群：81035754