摘要：如果不一致，那么就出現(xiàn)了新的機器學習問題，如等。要解決獨立同分布的問題，理論正確的方法就是對每一層的數(shù)據(jù)都進行白化操作。變換為均值為方差為的分布，也并不是嚴格的同分布，只是映射到了一個確定的區(qū)間范圍而已。

“ 深度神經網(wǎng)絡模型訓練之難眾所周知，其中一個重要的現(xiàn)象就是 Internal Covariate Shift. Batch Normalization 大法自 2015 年由Google 提出之后，就成為深度學習必備之神器。自 BN 之后， Layer Norm / Weight Norm / Cosine Norm 等也橫空出世。本文從 Normalization 的背景講起，用一個公式概括 Normalization 的基本思想與通用框架，將各大主流方法一一對號入座進行深入的對比分析，并從參數(shù)和數(shù)據(jù)的伸縮不變性的角度探討 Normalization 有效的深層原因。本文是該系列的第一篇。”

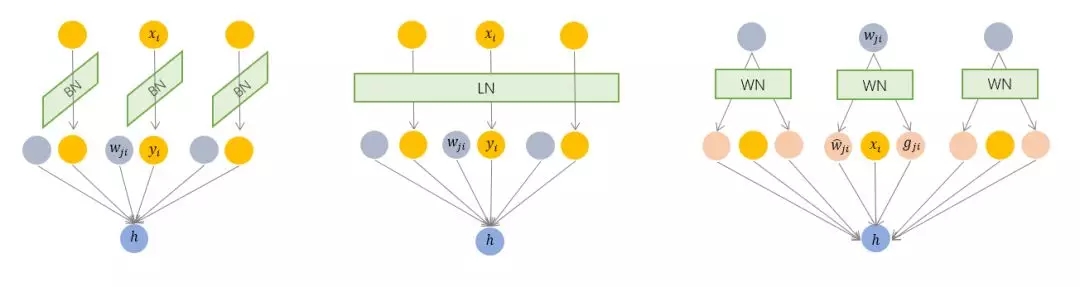
01、為什么需要 Normalization

1.1 ?獨立同分布與白化

機器學習界的煉丹師們最喜歡的數(shù)據(jù)有什么特點？竊以為，莫過于“獨立同分布”了，即 independent and identically distributed，簡稱為 i.i.d. 獨立同分布并非所有機器學習模型的必然要求（比如 Naive Bayes 模型就建立在特征彼此獨立的基礎之上，而Logistic Regression 和 神經網(wǎng)絡 則在非獨立的特征數(shù)據(jù)上依然可以訓練出很好的模型），但獨立同分布的數(shù)據(jù)可以簡化常規(guī)機器學習模型的訓練、提升機器學習模型的預測能力，已經是一個共識。

因此，在把數(shù)據(jù)喂給機器學習模型之前，“白化（whitening）”是一個重要的數(shù)據(jù)預處理步驟。白化一般包含兩個目的：

（1）去除特征之間的相關性 —> 獨立；

（2）使得所有特征具有相同的均值和方差 —> 同分布。

白化最典型的方法就是PCA，本文不再展開。

1.2 深度學習中的 Internal Covariate Shift

深度神經網(wǎng)絡模型的訓練為什么會很困難？其中一個重要的原因是，深度神經網(wǎng)絡涉及到很多層的疊加，而每一層的參數(shù)更新會導致上層的輸入數(shù)據(jù)分布發(fā)生變化，通過層層疊加，高層的輸入分布變化會非常劇烈，這就使得高層需要不斷去重新適應底層的參數(shù)更新。為了訓好模型，我們需要非常謹慎地去設定學習率、初始化權重、以及盡可能細致的參數(shù)更新策略。

Google 將這一現(xiàn)象總結為 Internal Covariate Shift，簡稱 ICS. 什么是 ICS 呢？@魏秀參 在一個回答中做出了一個很好的解釋：

大家都知道在統(tǒng)計機器學習中的一個經典假設是“源空間（source domain）和目標空間（target domain）的數(shù)據(jù)分布（distribution）是一致的”。如果不一致，那么就出現(xiàn)了新的機器學習問題，如 transfer learning / domain adaptation 等。而 covariate shift 就是分布不一致假設之下的一個分支問題，它是指源空間和目標空間的條件概率是一致的，但是其邊緣概率不同，即：對所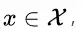有有：

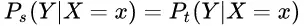
但是

大家細想便會發(fā)現(xiàn)，的確，對于神經網(wǎng)絡的各層輸出，由于它們經過了層內操作作用，其分布顯然與各層對應的輸入信號分布不同，而且差異會隨著網(wǎng)絡深度增大而增大，可是它們所能“指示”的樣本標記（label）仍然是不變的，這便符合了 covariate shift 的定義。由于是對層間信號的分析，也即是 “internal”的來由。

1.3 ICS 會導致什么問題？

簡而言之，每個神經元的輸入數(shù)據(jù)不再是“獨立同分布”。

其一，上層參數(shù)需要不斷適應新的輸入數(shù)據(jù)分布，降低學習速度。

其二，下層輸入的變化可能趨向于變大或者變小，導致上層落入飽和區(qū)，使得學習過早停止。

其三，每層的更新都會影響到其它層，因此每層的參數(shù)更新策略需要盡可能的謹慎。

02、Normalization 的基本思想與框架

我們以神經網(wǎng)絡中的一個普通神經元為例。神經元接收一組輸入向量

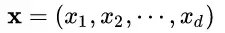
通過某種運算后，輸出一個標量值：

由于 ICS 問題的存在， x 的分布可能相差很大。要解決獨立同分布的問題，“理論正確”的方法就是對每一層的數(shù)據(jù)都進行白化操作。然而標準的白化操作代價高昂，特別是我們還希望白化操作是可微的，保證白化操作可以通過反向傳播來更新梯度。

因此，以 BN 為代表的 Normalization 方法退而求其次，進行了簡化的白化操作。基本思想是：在將 x 送給神經元之前，先對其做平移和伸縮變換， 將 x 的分布規(guī)范化成在固定區(qū)間范圍的標準分布。

通用變換框架就如下所示：

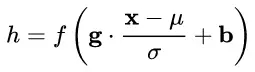
我們來看看這個公式中的各個參數(shù)。

（1） μ 是平移參數(shù)（shift parameter）， σ 是縮放參數(shù)（scale parameter）。通過這兩個參數(shù)進行 shift 和 scale 變換：?

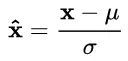
得到的數(shù)據(jù)符合均值為 0、方差為 1 的標準分布。

（2）b 是再平移參數(shù)（re-shift parameter），b 是再縮放參數(shù)（re-scale parameter）。將 上一步得到的 hat{x} 進一步變換為：?

最終得到的數(shù)據(jù)符合均值為 b 、方差為 g^2 的分布。

奇不奇怪？奇不奇怪？

說好的處理 ICS，第一步都已經得到了標準分布，第二步怎么又給變走了？

答案是——為了保證模型的表達能力不因為規(guī)范化而下降。

我們可以看到，第一步的變換將輸入數(shù)據(jù)限制到了一個全局統(tǒng)一的確定范圍（均值為 0、方差為 1）。下層神經元可能很努力地在學習，但不論其如何變化，其輸出的結果在交給上層神經元進行處理之前，將被粗暴地重新調整到這一固定范圍。

沮不沮喪？沮不沮喪？

難道我們底層神經元人民就在做無用功嗎？

所以，為了尊重底層神經網(wǎng)絡的學習結果，我們將規(guī)范化后的數(shù)據(jù)進行再平移和再縮放，使得每個神經元對應的輸入范圍是針對該神經元量身定制的一個確定范圍（均值為 b 、方差為 g^2 ）。rescale 和 reshift 的參數(shù)都是可學習的，這就使得 Normalization 層可以學習如何去尊重底層的學習結果。

除了充分利用底層學習的能力，另一方面的重要意義在于保證獲得非線性的表達能力。Sigmoid 等激活函數(shù)在神經網(wǎng)絡中有著重要作用，通過區(qū)分飽和區(qū)和非飽和區(qū)，使得神經網(wǎng)絡的數(shù)據(jù)變換具有了非線性計算能力。而第一步的規(guī)范化會將幾乎所有數(shù)據(jù)映射到激活函數(shù)的非飽和區(qū)（線性區(qū)），僅利用到了線性變化能力，從而降低了神經網(wǎng)絡的表達能力。而進行再變換，則可以將數(shù)據(jù)從線性區(qū)變換到非線性區(qū)，恢復模型的表達能力。

那么問題又來了——

經過這么的變回來再變過去，會不會跟沒變一樣？

不會。因為，再變換引入的兩個新參數(shù) g 和 b，可以表示舊參數(shù)作為輸入的同一族函數(shù)，但是新參數(shù)有不同的學習動態(tài)。在舊參數(shù)中， x 的均值取決于下層神經網(wǎng)絡的復雜關聯(lián)；但在新參數(shù)中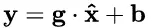，?僅由 b 來確定，去除了與下層計算的密切耦合。新參數(shù)很容易通過梯度下降來學習，簡化了神經網(wǎng)絡的訓練。

那么還有一個問題（問題怎么這么多！）——

這樣的 Normalization 離標準的白化還有多遠？

標準白化操作的目的是“獨立同分布”。獨立就不說了，暫不考慮。變換為均值為 b 、方差為 g^2 的分布，也并不是嚴格的同分布，只是映射到了一個確定的區(qū)間范圍而已。（所以，這個坑還有得研究呢！）

商業(yè)智能與數(shù)據(jù)分析群

興趣范圍包括各種讓數(shù)據(jù)產生價值的辦法，實際應用案例分享與討論，分析工具，ETL工具，數(shù)據(jù)倉庫，數(shù)據(jù)挖掘工具，報表系統(tǒng)等全方位知識

QQ群：81035754