摘要：本文試圖揭開讓人迷惘的云霧，領悟背后的原理和魅力，品嘗這一頓盛宴。當然，激活函數本身很簡單，比如一個激活的全連接層，用寫起來就是可是，如果我想用的反函數來激活呢也就是說，你得給我解出，然后再用它來做激活函數。

由深度學習先驅 Hinton 開源的 Capsule 論文 Dynamic Routing Between Capsules，無疑是去年深度學習界最熱點的消息之一。

得益于各種媒體的各種吹捧，Capsule 被冠以了各種神秘的色彩，諸如“拋棄了梯度下降”、“推倒深度學習重來”等字眼層出不窮，但也有人覺得 Capsule 不外乎是一個新的炒作概念。?

本文試圖揭開讓人迷惘的云霧，領悟 Capsule 背后的原理和魅力，品嘗這一頓 Capsule 盛宴。同時，筆者補做了一個自己設計的實驗，這個實驗能比原論文的實驗更有力說明 Capsule 的確產生效果了。

菜譜一覽：

Capsule 是什么？

Capsule 為什么要這樣做？

Capsule 真的好嗎？

我覺得 Capsule 怎樣？

若干小菜

前言

Capsule 的論文已經放出幾個月了，網上已經有很多大佬進行解讀，也有大佬開源實現了 CapsuleNet，這些內容都加速了我對 Capsule 的理解。然而，我覺得美中不足的是，網上多數的解讀，都只是在論文的翻譯上粉飾了一點文字，并沒有對 Capsule 的原理進行解讀。

比如“動態路由”那部分，基本上就是照搬論文的算法，然后說一下迭代3次就收斂了。但收斂出什么來？論文沒有說，解讀也沒有說，這顯然是不能讓人滿意的。也難怪知乎上有讀者評論說：

所謂的 Capsule 為 DL 又貢獻了一個花里胡哨的 trick 概念。說它是 trick，因為 Hinton 沒有說為什么 routing 算法為什么需要那么幾步，循環套著循環，有什么理論依據嗎？還是就是湊出來的？

這個評論雖然過激，然而也是很中肯的：憑啥 Hinton 擺出來一套算法又不解釋，我們就要稀里糊涂的跟著玩？

Capsule 盛宴

宴會特色?

這次 Capsule 盛宴的特色是“vector in vector out”，取代了以往的“scaler in scaler out”，也就是神經元的輸入輸出都變成了向量，從而算是對神經網絡理論的一次革命。

然而真的是這樣子嗎？難道我們以往就沒有做過“vector in vector out”的任務了嗎？

有，而且多的是！NLP 中，一個詞向量序列的輸入，不就可以看成“vector in”了嗎？這個詞向量序列經過 RNN/CNN/Attention 的編碼，輸出一個新序列，不就是“vector out”了嗎？

在目前的深度學習中，從來不缺乏“vector in vector out”的案例，因此顯然這不能算是 Capsule 的革命。?

Capsule 的革命在于：它提出了一種新的“vector in vector out”的傳遞方案，并且這種方案在很大程度上是可解釋的。?

如果問深度學習（神經網絡）為什么有效，我一般會這樣回答：神經網絡通過層層疊加完成了對輸入的層層抽象，這個過程某種程度上模擬了人的層次分類做法，從而完成對最終目標的輸出，并且具有比較好的泛化能力。

的確，神經網絡應該是這樣做的，然而它并不能告訴我們它確確實實是這樣做的，這就是神經網絡的難解釋性，也就是很多人會將深度學習視為黑箱的原因之一。?

讓我們來看 Hinton 是怎么來通過 Capsule 突破這一點的。

大盆菜

如果要用一道菜來比喻 Capsule，我想到了“大盆菜”：

盆菜作為客家菜的菜式出現由來以久，一般也稱為大盤菜，大盤菜源于客家人傳統的“發財大盤菜”，顧名思義就是用一個大大的盤子，將食物都放到里面，融匯出一種特有滋味。豐富的材料一層層疊進大盤之中，最易吸收肴汁的材料通常放在下面。吃的時候每桌一盤，一層一層吃下去，汁液交融，味道馥郁而香濃，令人大有漸入佳景之快。

Capsule 就是針對著這個“層層遞進”的目標來設計的，但坦白說，Capsule 論文的文筆真的不敢恭維，因此本文盡量不與論文中的符號相同，以免讀者再次云里霧里。讓我們來看個圖。

如圖所示，底層的膠囊和高層的膠囊構成一些連接關系。等等，什么是“膠囊”？其實，只要把一個向量當作一個整體來看，它就是一個“膠囊”，是的，你沒看錯，你可以這樣理解：神經元就是標量，膠囊就是向量，就這么粗暴。

Hinton 的理解是：每一個膠囊表示一個屬性，而膠囊的向量則表示這個屬性的“標架”。

也就是說，我們以前只是用一個標量表示有沒有這個特征（比如有沒有羽毛），現在我們用一個向量來表示，不僅僅表示有沒有，還表示“有什么樣的”（比如有什么顏色、什么紋理的羽毛），如果這樣理解，就是說在對單個特征的表達上更豐富了。?

說到這里，我感覺有點像 NLP 中的詞向量，以前我們只是用 one hot 來表示一個詞，也就是表示有沒有這個詞而已。現在我們用詞向量來表示一個詞，顯然詞向量表達的特征更豐富，不僅可以表示有沒有，還可以表示哪些詞有相近含義。詞向量就是NLP中的“膠囊”？這個類比可能有點牽強，但我覺得意思已經對了。?

那么，這些膠囊要怎么運算，才能體現出“層層抽象”、“層層分類”的特性呢？讓我們先看其中一部分連接：

圖上只展示了 u1 的連接。這也就是說，目前已經有了 u1 這個特征（假設是羽毛），那么我想知道它屬于上層特征 v1,v2,v3,v4（假設分別代表了雞、鴨、魚、狗）中的哪一個。

分類問題我們顯然已經是很熟悉了，不就是內積后 softmax 嗎？于是單靠 u1 這個特征，我們推導出它是屬于雞、鴨、魚、狗的概率分別是：

我們當然期望 p(1|1) 和 p(2|1) 會明顯大于 p(3|1) 和 p(4|1)。

不過，單靠這個特征還不夠，我們還需要綜合各個特征，于是可以把上述操作對各個 ui 都做一遍，繼而得到 [p(1|2),p(2|2),p(3|2),p(4|2)]、[p(1|3),p(2|3),p(3|3),p(4|3)]...

問題是，現在得到這么多預測結果，那我究竟要選擇哪個呢？而且我又不是真的要做分類，我要的是融合這些特征，構成更高級的特征。

于是 Hinton 認為，既然 ui 這個特征得到的概率分布是 [p(1|i),p(2|i),p(3|i),p(4|i)]，那么我把這個特征切成四份，分別為 [p(1|i)ui,p(2|i)ui,p(3|i)ui,p(4|i)ui]，然后把這幾個特征分別傳給 v1,v2,v3,v4，最后 v1,v2,v3,v4 其實就是各個底層傳入的特征的累加，這樣不就好了？

從上往下看，那么 Capsule 就是每個底層特征分別做分類，然后將分類結果整合。這時 vj 應該盡量與所有 ui 都比較靠近，靠近的度量是內積。

因此，從下往上看的話，可以認為 vj 實際上就是各個 ui 的某個聚類中心，而 Capsule 的核心思想就是輸出是輸入的某種聚類結果。

現在來看這個 squashing 是什么玩意，它怎么來的呢？

濃縮果汁

squash 在英文中也有濃縮果汁之意，我們就當它是一杯果汁品嘗吧。這杯果汁的出現，是因為 Hinton 希望 Capsule 能有的一個性質是：膠囊的模長能夠代表這個特征的概率。

其實我不喜歡概率這個名詞，因為概率讓我們聯想到歸一化，而歸一化事實上是一件很麻煩的事情。我覺得可以稱為是特征的“顯著程度”，這就好解釋了，模長越大，這個特征越顯著。

而我們又希望有一個有界的指標來對這個“顯著程度”進行衡量，所以就只能對這個模長進行壓縮了，所謂“濃縮就是精華”嘛。Hinton 選取的壓縮方案是：

其中 x/‖x‖ 是很好理解的，就是將模長變為 1，那么前半部分怎么理解呢？為什么這樣選擇？事實上，將模長壓縮到 0-1 的方案有很多，比如：

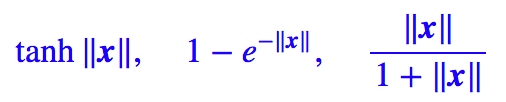
等等，并不確定 Hinton 選擇目前這個方案的思路。也許可以每個方案都探索一下？事實上，我在一些實驗中發現：

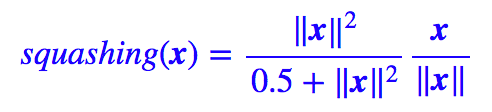
選擇上述函數的效果要好一點。這個函數的特點是在模長很接近于 0 時起到放大作用，而不像原來的函數那樣全局都壓縮。

然而，一個值得思考的問題是：如果在中間層，那么這個壓縮處理是不是必要的呢？

因為已經有了后面說的動態路由在里邊，因此即使去掉 squashing 函數，網絡也已經具有了非線性了，因此直覺上并沒有必要在中間層也引入特征壓縮，正如普通神經網絡也不一定要用 sigmoid 函數壓縮到 0-1。我覺得這個要在實踐中好好檢驗一下。

動態路由

注意到（2）式，為了求 vj 需要求 softmax，可是為了求 softmax 又需要知道 vj，這不是個雞生蛋、蛋生雞的問題了嗎？

這時候就要上“主菜”了，即“動態路由”（Dynamic Routing），它能夠根據自身的特性來更新（部分）參數，從而初步達到了 Hinton 的放棄梯度下降的目標。?

這道“主菜”究竟是是不是這樣的呢？它是怎么想出來的？最終收斂到哪里去？讓我們先上兩道小菜，然后再慢慢來品嘗這道主菜。

小菜 1

讓我們先回到普通的神經網絡，大家知道，激活函數在神經網絡中的地位是舉足輕重的。當然，激活函數本身很簡單，比如一個 tanh 激活的全連接層，用 TensorFlow 寫起來就是：

y = tf.matmul(W, x) + b

y = tf.tanh(y)

可是，如果我想用 x=y+cos y 的反函數來激活呢？也就是說，你得給我解出 y=f(x)，然后再用它來做激活函數。

然而數學家告訴我們，這個東西的反函數是一個超越函數，也就是不可能用初等函數有限地表示出來。那這樣不就是故意刁難么？不要緊，我們有迭代：

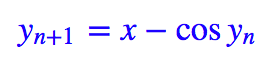
選擇 y0=x，代入上式迭代幾次，基本上就可以得到比較準確的 y 了。假如迭代三次，那就是：

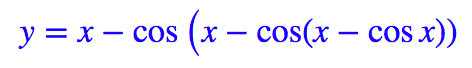
用 TensorFlow 寫出來就是：

y = tf.matmul(W, x) + b

Y=y

for i in range(3):

? ? Y = y - tf.cos(Y)

如果讀者已經“預習”過 Capsule，那么就會發現這跟 Capsule 的動態路由很像。?

小菜 2

再來看一個例子，這個例子可能在 NLP 中有很多對應的情景，但圖像領域其實也不少。考慮一個向量序列 (x1,x2,…,xn)，我現在要想辦法將這 n 個向量整合成一個向量 x（encoder），然后用這個向量來做分類。

也許讀者會想到用LSTM。但我這里僅僅想要將它表示為原來向量的線性組合，也就是：

這里的 λi 相當于衡量了 x 與 xi 的相似度。然而問題來了，在 x 出現之前，憑什么能夠確定這個相似度呢？這不也是一個雞生蛋、蛋生雞的問題嗎？

解決這個問題的一個方案也是迭代。首先我們也可以定義一個基于 softmax 的相似度指標，然后讓：

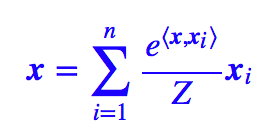
一開始，我們一無所知，所以只好取 x 為各個 xi 的均值，然后代入右邊就可以算出一個 x，再把它代入右邊，反復迭代就行，一般迭代有限次就可以收斂，于是就可以將這個迭代過程嵌入到神經網絡中了。

如果說小菜 1 跟動態路由只是神似，那么小菜 2 已經跟動態路由是神似＋形似了。不過我并沒有看到已有的工作是這樣做的，這個小菜只是我的頭腦風暴。

上主菜

其實有了這兩個小菜，動態路由這道主菜根本就不神秘了。為了得到各個 vj，一開始先讓它們全都等于 ui 的均值，然后反復迭代就好。說白了，輸出是輸入的聚類結果，而聚類通常都需要迭代算法，這個迭代算法就稱為“動態路由”。

至于這個動態路由的細節，其實是不固定的，取決于聚類的算法，比如關于 Capsule 的新文章 MATRIX CAPSULES WITH EM ROUTING 就使用了 Gaussian Mixture Model 來聚類。?

理解到這里，就可以寫出本文的動態路由的算法了：

這里的 cij 就是前文的 p(j|i)。

“嘿，終于逮到個錯誤了，我看過論文，應該是 bij=bij+ui?vj 而不是 bij=ui?vj 吧”？

事實上，上述算法并沒有錯——如果你承認本文的推導過程、承認（2）式的話，那么上述迭代過程就是沒有錯的。

“難道是Hinton錯了？就憑你也有資格向Hinton叫板”？別急別急，先讓我慢慢分析 Hinton 的迭代出現了什么問題。

假如按照 Hinton 的算法，那么是 bij=bij+ui?vj，從而經過 r 次迭代后，就變成了：

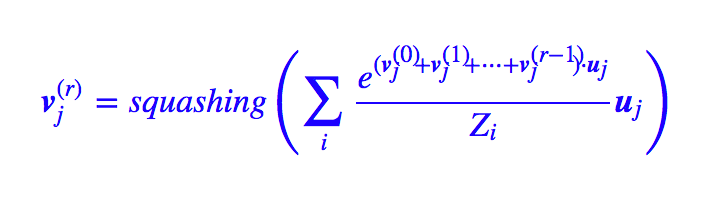
由于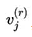會越來越接近真實的 vj，那么我們可以寫出：

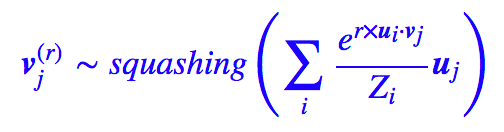
假如經過無窮多次迭代（實際上算力有限，做不到，但理論上總可以做到的），那么 r→∞，這樣的話 softmax 的結果是非零即 1，也就是說，每個底層的膠囊僅僅聯系到一個上層膠囊。這時候 vj 已不再是聚類中心，而是距離它們聚類中心最近的那個 ui。

這合理嗎？我覺得很不合理。不同的類別之間是有可能有共同的特征的，這就好比人和動物雖然不一樣，但是都有眼睛。

對于這個問題，有些朋友是這樣解釋的：r 是一個超參數，不能太大，太大了就容易過擬合。首先我不知道 Hinton 是不是也是同樣的想法，但我認為，如果認為 r 是一個超參，那么這將會使得 Capsule 太丑陋了。

是啊，動態路由被來已經被很多讀者評價為“不知所云”了，如果加上完全不符合直覺的超參，不就更加難看了嗎？

相反，如果換成本文的（2）式作為出發點，然后得到本文的動態路由算法，才能符合聚類的思想，而且在理論上會好看些，因為這時候就是 r 越大越好了（看算力而定），不存在這個超參。

事實上，我改動了之后，在目前開源的 Capsule 源碼上跑，也能跑到同樣的結果。

至于讀者怎么選擇，就看讀者的意愿吧。我自己是有點強迫癥的，忍受不了理論上的不足。

模型細節

下面介紹 Capsule 實現的細節，對應的代碼在我的 Github 中，不過目前只有 Keras 版。相比之前實現的版本，我的版本是純 Keras 實現的（原來是半 Keras 半 TensorFlow），并通過 K.local_conv1d 函數替代了 K.map_fn 提升了好幾倍的速度。

這是因為 K.map_fn 并不會自動并行，要并行的話需要想辦法整合到一個矩陣運算；其次我通過 K.conv1d 實現了共享參數版的。代碼要在 Keras 2.1.0 以上版本運行。

全連接版

先不管是 Hinton 版還是我的版本，按照這個動態路由的算法，vj 能夠迭代地算出來，那不就沒有參數了嗎？真的拋棄了反向傳播了？

非也非也，如果真的這樣的話，各個 vj 都一樣了。前面已經說了，vj 是作為輸入 ui 的某種聚類中心出現的，而從不同角度看輸入，得到的聚類結果顯然是不一樣的。

那么為了實現“多角度看特征”，可以在每個膠囊傳入下一個膠囊之前，都要先乘上一個矩陣做變換，所以（2）式實際上應該要變為：

這里的 Wji 是待訓練的矩陣，這里的乘法是矩陣乘法，也就是矩陣乘以向量。所以，Capsule 變成了下圖。

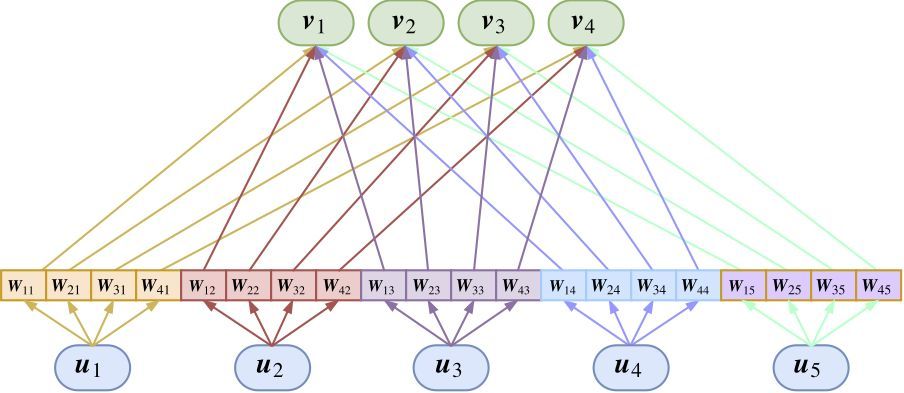
這時候就可以得到完整動態路由了。

這樣的 Capsule 層，顯然相當于普通神經網絡中的全連接層。

共享版

眾所周知，全連接層只能處理定長輸入，全連接版的 Capsule 也不例外。而 CNN 處理的圖像大小通常是不定的，提取的特征數目就不定了，這種情形下，全連接層的 Capsule 就不適用了。

因為在前一圖就可以看到，參數矩陣的個數等于輸入輸入膠囊數目乘以輸出膠囊數目，既然輸入數目不固定，那么就不能用全連接了。

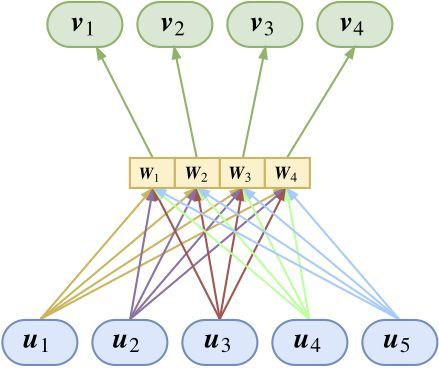
所以跟 CNN 的權值共享一樣，我們也需要一個權值共享版的 Capsule。所謂共享版，是指對于固定的上層膠囊 j，它與所有的底層膠囊的連接的變換矩陣是共用的，即 Wji≡Wj。

如圖所示，共享版其實不難理解，就是自下而上地看，所有輸入向量經過同一個矩陣進行映射后，完成聚類進行輸出，將這個過程重復幾次，就輸出幾個向量（膠囊）。

又或者自上而下地看，將每個變換矩陣看成是上層膠囊的識別器，上層膠囊通過這個矩陣來識別出底層膠囊是不是有這個特征。

因此很明顯，這個版本的膠囊的參數量并不依賴于輸入的膠囊個數，因此可以輕松接在 CNN 后面。對于共享版，（2）式要變為：

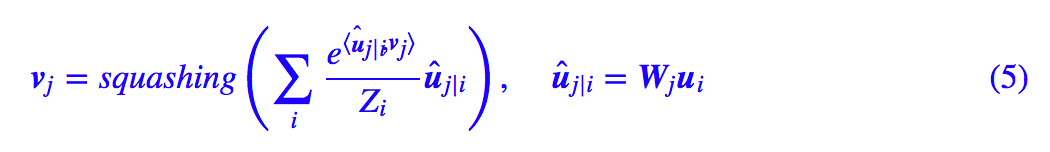
至于動態路由算法就沒有改變了。

反向傳播?

盡管我不是很喜歡反向傳播這個名詞，然而這里似乎不得不用上這個名字了。?

現在又有了 Wji，那么這些參數怎么訓練呢？答案是反向傳播。讀者也許比較暈的是：現在既有動態路由，又有反向傳播了，究竟兩者怎么配合？

其實這個真的就最簡單不過了。就好像“小菜 1”那樣，把算法的迭代幾步（論文中是 3 步），加入到模型中，從形式上來看，就是往模型中添加了三層罷了，剩下的該做什么還是什么，最后構建一個 loss 來反向傳播。?

這樣看來，Capsule 里邊不僅有反向傳播，而且只有反向傳播，因為動態路由已經作為了模型的一部分，都不算在迭代算法里邊了。?

做了什么?

是時候回顧一下了，Capsule 究竟做了什么？其實用一種最直接的方式來講，Capsule 就是提供了一種新的“vector in vector out”的方案，這樣看跟 CNN、RNN、Attention 層都沒太大區別了。

從 Hinton 的本意看，就是提供了一種新的、基于聚類思想來代替池化完成特征的整合的方案，這種新方案的特征表達能力更加強大。

實驗

MNIST 分類

不出意外地，Capsule 首先被用在 MNIST 中做實驗，然后效果還不錯，通過擾動膠囊內的一些值來重構圖像，確實發現這些值代表了某種含義，這也體現了 Capsule 初步完成了它的目標。

Capsule 做分類模型，跟普通神經網絡的一些區別是：Capsule 最后輸出 10 個向量（也就是 10 個膠囊），這 10 個向量各代表一類，每個向量的模長代表著它的概率。

事實上，Capsule 做的事情就是檢測有沒有這個類，也就是說，它把一個多分類問題轉化為多個 2 分類問題。因此它并沒有用普通的交叉熵損失，而是用了：

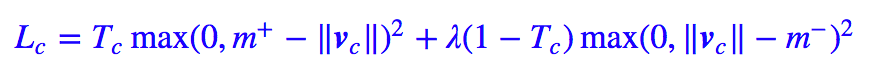
其中 Tc 非零即 1，表明是不是這個類。當然這個沒什么特殊性，也可以有多種選擇。論文中還對比了加入重構網絡后的提升。?

總的來說，論文的實驗有點粗糙，選擇 MNIST 來做實驗顯得有點不給力（好歹也得玩玩 fashion MNIST 嘛），重構網絡也只是簡單粗暴地堆了兩層全連接來做。不過就論文的出發點，應該只要能證明這個流程能 work 就好了，因此差強人意吧。?

我的實驗?

由于普通的卷積神經網絡下，MNIST 的驗證集準確率都已經 99%+ 了，因此如果就這樣說 Capsule 起作用了，難免讓人覺得不服氣。

這里我為 Capsule 設計了一個新實驗，雖然這個實驗也是基于 MNIST，但這個實驗很充分地說明了 Capsule 具有良好的整合特征的能力。Capsule 不僅 work，還 work 得很漂亮。

具體實驗如下：

1. 通過現有的 MNIST 數據集，訓練一個數字識別模型，但最后不用 softmax 做 10 分類，而是轉化為 10 個 2 分類問題；

2. 訓練完模型后，用模型進行測試。測試的圖片并不是原始的測試集，是隨機挑兩張測試集的圖片拼在一起，然后看模型能不能預測出這兩個數字來（數字對即可，不考慮順序）。

也就是說，訓練集是 1 對 1 的，測試集是 2 對 2 的。

實驗用 Keras 完成，完成的代碼可見我的 Github。這里僅僅展示核心部分。

Github: https://github.com/bojone/Capsule

首先是 CNN。公平起見，大家的 CNN 模型都是一樣的。

#CNN部分，這部分兩個模型都一致

input_image = Input(shape=(None,None,1))

cnn = Conv2D(64, (3, 3), activation="relu")(input_image)

cnn = Conv2D(64, (3, 3), activation="relu")(cnn)

cnn = AveragePooling2D((2,2))(cnn)

cnn = Conv2D(128, (3, 3), activation="relu")(cnn)

cnn = Conv2D(128, (3, 3), activation="relu")(cnn)

然后先用普通的 Pooling + 全連接層進行建模：

cnn = GlobalAveragePooling2D()(cnn)

dense = Dense(128, activation="relu")(cnn)

output = Dense(10, activation="sigmoid")(dense)

model = Model(inputs=input_image, outputs=output)

model.compile(loss=lambda y_true,y_pred: y_true*K.relu(0.9-y_pred)**2 + 0.25*(1-y_true)*K.relu(y_pred-0.1)**2,

? ? ? ? ? ? ? optimizer="adam",

? ? ? ? ? ? ? metrics=["accuracy"])

這個代碼的參數量約為 27 萬，能在 MNIST 的標準測試集上達到 99.3% 以上的準確率，顯然已經接近較佳狀態。

下面測試我們開始制定的任務，我們最后輸出兩個準確率：第一個準確率是取分數較高的兩個類別；第二個準確率是取得分較高的兩個類別，并且這兩個類別的分數都要超過 0.5 才認可（因為是 2 分類）。代碼如下：

#對測試集重新排序并拼接到原來測試集，就構成了新的測試集，每張圖片有兩個不同數字

idx = range(len(x_test))

np.random.shuffle(idx)

X_test = np.concatenate([x_test, x_test[idx]], 1)

Y_test = np.vstack([y_test.argmax(1), y_test[idx].argmax(1)]).T

X_test = X_test[Y_test[:,0] != Y_test[:,1]] #確保兩個數字不一樣

Y_test = Y_test[Y_test[:,0] != Y_test[:,1]]

Y_test.sort(axis=1) #排一下序，因為只比較集合，不比較順序

Y_pred = model.predict(X_test) #用模型進行預測

greater = np.sort(Y_pred, axis=1)[:,-2] > 0.5 #判斷預測結果是否大于0.5

Y_pred = Y_pred.argsort()[:,-2:] #取較高分數的兩個類別

Y_pred.sort(axis=1) #排序，因為只比較集合

acc = 1.*(np.prod(Y_pred == Y_test, axis=1)).sum()/len(X_test)

print u"不考慮置信度的準確率為：%s"%acc

acc = 1.*(np.prod(Y_pred == Y_test, axis=1)*greater).sum()/len(X_test)

print u"考慮置信度的準確率為：%s"%acc

經過重復測試，如果不考慮置信度，那么準確率大約為 40%，如果考慮置信度，那么準確率是 10% 左右。這是一組保守的數據，反復測試幾次的話，很多時候連這兩個都不到。

現在我們來看 Capsule 的表現，將 CNN 后面的代碼替換成：

capsule = Capsule(10, 16, 3, True)(cnn)

output = Lambda(lambda x: K.sqrt(K.sum(K.square(x), 2)))(capsule)

model = Model(inputs=input_image, outputs=output)

model.compile(loss=lambda y_true,y_pred: y_true*K.relu(0.9-y_pred)**2 + 0.25*(1-y_true)*K.relu(y_pred-0.1)**2,

? ? ? ? ? ? ? optimizer="adam",

? ? ? ? ? ? ? metrics=["accuracy"])

這里用的就是共享權重版的 Capsule，最后輸出向量的模長作為分數，loss 和 optimizer 都跟前面一致，代碼的參數量也約為 27 萬，在 MNIST 的標準測試集上的準確率同樣也是 99.3% 左右，這部分兩者都差不多。

然而，讓人驚訝的是：在前面所定制的新測試集上，Capsule 模型的兩個準確率都有 90% 以上。即使我們沒有針對性地訓練，但 Capsule 仍以高置信度給出了輸入中包含的特征（即哪個數字）。

也就是說，我們訓練了單個數字的識別模型，卻有可能直接得到一個同時識別多數字的模型，這顯然很符合人類的學習能力。

事實上我們還可以更細致地分析特征的流動情況，確定數字的順序（而不單單是當成一個集合來識別），從而構成一個完整的多數字識別模型。這很大程度上得益于 Capsule 的可解釋性，也表明 Capsule 確確實實形成了良好的特征表達，減少了信息損失。

思考

看起來還行

Capsule 致力于給出神經網絡的可解釋的方案，因此，從這個角度來看，Capsule 應該是成功的，至少作為測試版是很成功的。因為它的目標并不是準確率非常出眾，而是對輸入做一個優秀的、可解釋的表征。

從我上面的實驗來看，Capsule 也是很漂亮的，至少可以間接證明它比池化過程更接近人眼的機制。

事實上，通過向量的模長來表示概率，這一點讓我想起了量子力學的波函數，它也是通過波函數的范數來表示概率的。這告訴我們，未來 Capsule 的發展也許可以參考一下量子力學的內容。

亟待優化

顯然，Capsule 可優化的地方還有非常多，包括理論上的和實踐上的。我覺得整個算法中最不好看的部分并非動態路由，而是那個 squashing 函數。對于非輸出層，這個壓縮究竟是不是必要的？

還有，由于要用模長并表示概率，模長就得小于 1，而兩個模長小于 1 的向量加起來后模長不一定小于 1，因此需要用函數進一步壓縮，這個做法的主觀性太強。

這也許需要借助流形上的分析工具，才能給出更漂亮的解決方案，或者也可以借鑒一下量子力學的思路，因為量子力學也存在波函數相加的情況。

實踐角度來看，Capsule 顯然是太慢了。這是因為將動態路由的迭代過程嵌入了神經網絡中。從前向傳播來看，這并沒有增加多少計算量，但從反向傳播來看，計算量暴增了，因為復合函數的梯度會更加復雜。

反向傳播好不好？

Hinton 想要拋棄反向傳播的大概原因是：反向傳播在生物中找不到對應的機制，因為反向傳播需要較精確地求導數。

事實上，我并不認同這種觀點。盡管較精確求導在自然界中很難存在，但這才意味著我們的先進。

試想一下，如果不求導，那么我們也可以優化的，但需要“試探＋插值”，比如將參數 α 從 3 改為 5 后，發現 loss 變小了，于是我們就會想著試試 α=7，如果這時候 loss 變大了，我們就會想著試試 α=6。

loss 變小/大就意味著（近似的）梯度為負/正，這個過程的思想跟梯度下降是一致的，但這個過程一次性只能調節一個參數，而我們可能有數百萬的參數要調，需要進行上百萬次試驗要才能完成每一個參數的調整。

而求梯度，就是一種比重復試探更加高明的技巧，何樂而不用呢？

池化好不好？

Hinton 因為卷積中的池化是不科學的，但我并不這樣認為。也許對于 MNIST 這個 28*28 的數據集并不需要池化也能 work，但如果是 1000*1000 的大圖呢？越遠的東西就越看不清，這難道不是池化的結果？

所以我認為池化也是可取的，不過池化應該對低層的特征進行，高層的信息池化可能就會有問題了。

退一步講，如果堅決不用池化，那我用 stride=2 的卷積，不跟 stride=1 的卷積后接一個大小為 2 的池化是類似的嗎？筆者前面的 Capsule 實驗中，也將池化跟 Capsule 配合使用了，效果也沒有變糟。

結語

這應該是到目前為止我寫的最長的單篇文章了，不知道大家對這個 Capsule 飯局滿不滿意呢？

最后不得不吐槽一下，Hinton 真會起名字，把神經網絡重新叫做深度學習，然后深度學習就火了，現在把聚類的迭代算法放到神經網絡中，稱之為做動態路由，不知道會不會再次重現深度學習的輝煌呢？

商業智能與數據分析群

興趣范圍包括各種讓數據產生價值的辦法，實際應用案例分享與討論，分析工具，ETL工具，數據倉庫，數據挖掘工具，報表系統等全方位知識

QQ群：81035754