斯蒂文認(rèn)為機(jī)器學(xué)習(xí)有時(shí)候像嬰兒學(xué)習(xí)，特別是在物體識(shí)別上。比如嬰兒首先學(xué)會(huì)識(shí)別邊界和顏色，然后將這些信息用于識(shí)別形狀和圖形等更復(fù)雜的實(shí)體。比如在人臉識(shí)別上，他們學(xué)會(huì)從眼睛和嘴巴開(kāi)始識(shí)別最終到整個(gè)面孔。當(dāng)他們看一個(gè)人的形象時(shí)，他們大腦認(rèn)出了兩只眼睛，一只鼻子和一只嘴巴，當(dāng)認(rèn)出所有這些存在于臉上的實(shí)體，并且覺(jué)得“這看起來(lái)像一個(gè)人”。

斯蒂文首先給他的女兒悠悠看了以下圖片，看她是否能自己學(xué)會(huì)認(rèn)識(shí)圖中的人(金·卡戴珊)。

斯蒂文接下來(lái)用幾張圖來(lái)考她：

悠悠

圖中有兩只眼睛一個(gè)鼻子一張嘴巴，圖中的物體是個(gè)人。

斯蒂文

正確！

悠悠

圖中有兩只眼睛一個(gè)鼻子一張嘴巴，圖中的物體是個(gè)人。

斯蒂文

錯(cuò)誤！嘴巴長(zhǎng)到眼睛上還是個(gè)人嗎？

悠悠

圖中有一大塊都是黑色的，圖中的物體好像是頭發(fā)。

斯蒂文

錯(cuò)誤！這只是把第一張圖顛倒一下，怎么就變成頭發(fā)了？

斯蒂文很失望，覺(jué)得她第二、三張都應(yīng)該答對(duì)，但是他對(duì)悠悠要求太高了，要知道現(xiàn)在深度學(xué)習(xí)里流行的卷積神經(jīng)網(wǎng)絡(luò) (convolutional neural network, CNN) 給出的答案也和悠悠一樣，如下：

第一張 CNN 給出的答案是人，概率為 0.88，正確；第二張 CNN 給出的答案也是人，概率為 0.90 ，開(kāi)玩笑在？第三張 CNN 給出的答案是黑發(fā)，概率為 0.79 ，呵呵，和悠悠一樣天真。

?

CNN 弄錯(cuò)的兩張圖也是因?yàn)樗膬蓚€(gè)缺陷：

?

CNN 對(duì)物體之間的空間關(guān)系 (spatial relationship) 的識(shí)別能力不強(qiáng)，比如卡戴珊的嘴巴和眼睛換位置了還被識(shí)別成人？

CNN 對(duì)物體旋轉(zhuǎn)之后的識(shí)別能力不強(qiáng) (微微旋轉(zhuǎn)還可以)，比如卡戴珊倒過(guò)來(lái)就被識(shí)別成頭發(fā)了？

?

Convolutional neural networks are doomed. -- Hinton

大神 Hinton 如此說(shuō)道“卷積神經(jīng)網(wǎng)絡(luò)要完蛋了”，因此他最近也提出了一個(gè) Capsule 的東西，直譯成膠囊。但是這個(gè)翻譯丟失了很多重要的東西，個(gè)人認(rèn)為叫做向量神經(jīng)元 (vector neuron) 甚至張量神經(jīng)元 (tensor neuron) 更貼切。正式介紹 Capsule 的這篇文章在 2017 年 11 月 7 日才出來(lái)，論文名字叫《Dynamic Routing Between Capsules》，有興趣的同學(xué)跟我走一遭吧。

目錄

第一章 - 前戲王

? ? 1.1 物體姿態(tài)

? ? 1.2 不變性和同變性

? ? 1.3 全連接層

? ? 1.4 卷積神經(jīng)網(wǎng)絡(luò)

第二章 - 理論皇

? ? 2.1 膠囊定義

? ? 2.2 神經(jīng)元類比

? ? 2.3 工作原理

? ? 2.4 動(dòng)態(tài)路由

? ? 2.5 網(wǎng)絡(luò)結(jié)構(gòu)

第三章 - 實(shí)踐狼

? ? 3.1 帆船房子

? ? 3.2 代碼解析

總結(jié)和下帖預(yù)告

1、前戲王

1.1

物體姿態(tài)

為了正確的分類和識(shí)別物體，保持物體部分之間的分層姿態(tài) (hierarchical pose) 關(guān)系是很重要的。姿態(tài)主要包括平移 (translation)、旋轉(zhuǎn) (rotation) 和放縮 (scale) 三種形式。

在拍攝人物時(shí)，我們調(diào)動(dòng)照相機(jī)的角度從 3D 的人生成 2D 的照片。照出來(lái)的人物照角度多種多樣，但人是個(gè)整體 (臉和身體對(duì)于人的相對(duì)位置不會(huì)變)。因此我們不想定義相對(duì)于相機(jī)的所有對(duì)象 (臉和身體)，而將它們定義一個(gè)相對(duì)穩(wěn)定的坐標(biāo)系 (coordinate frame) 中，然后僅僅通過(guò)轉(zhuǎn)動(dòng)相機(jī)來(lái)照出不同角度的照片。

在創(chuàng)建這些圖形時(shí)，我們首先會(huì)定義臉和身體相對(duì)于人的位置，更進(jìn)一層，我們會(huì)定義眼睛和嘴巴對(duì)于相對(duì)于臉的位置，但不是相對(duì)于人的位置。因?yàn)橹耙呀?jīng)有了臉相對(duì)于人的位置，現(xiàn)在又有了眼睛相對(duì)于臉的位置，那么也有了眼睛相對(duì)于人的位置。本質(zhì)上，你將有層次的創(chuàng)建一個(gè)完整的人，而所需要的數(shù)學(xué)工具就是姿態(tài)矩陣 (pose matrix)，這個(gè)矩陣定義所有對(duì)象相對(duì)于照相機(jī)的視點(diǎn) (viewpoint)，并且還表示了部件與整體之間的關(guān)系。

In order to correctly do classification and object recognition, it is important to preserve hierarchical pose relationships between object parts. -- Hinton

Hinton 認(rèn)為，為了正確地進(jìn)行分類和對(duì)象識(shí)別，重要的是保持對(duì)象部分之間的分層姿態(tài)關(guān)系。后面講到的 Capsule 就符合這個(gè)重要直覺(jué)，它結(jié)合了對(duì)象之間的相對(duì)關(guān)系，并以姿態(tài)矩陣來(lái)表示。

首先我們看看 2 維平面中姿態(tài)矩陣是如何平移、旋轉(zhuǎn)和放縮物體：

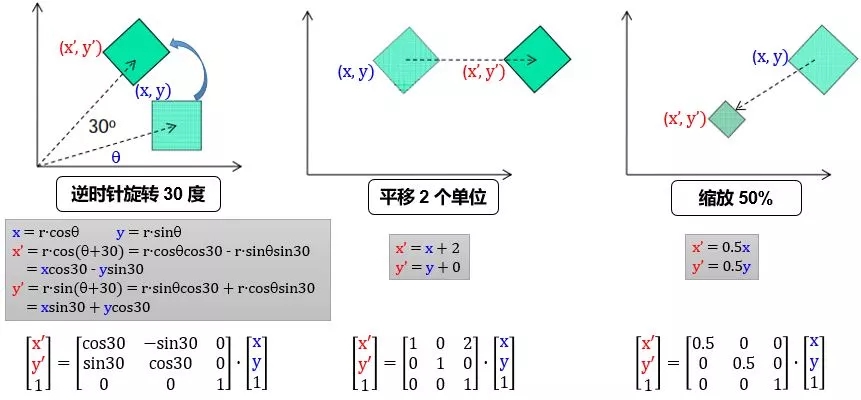
用 R, T, S 定義旋轉(zhuǎn)、平移和縮放矩陣，那么將 (x, y) 先逆時(shí)針轉(zhuǎn) 30 度，再向右平移 2 個(gè)單位，最后縮放 50% 到 (x", y") 可以由下列矩陣連乘得到

在 2 維平面中，我們加了 1 個(gè)維度 z，是為了方便完成平移操作。寫出 2 維平面姿態(tài)矩陣 M 的一般形式，并延伸并類比到 3 維空間的姿態(tài)矩陣，表示如下：

下面看個(gè)具體例子：

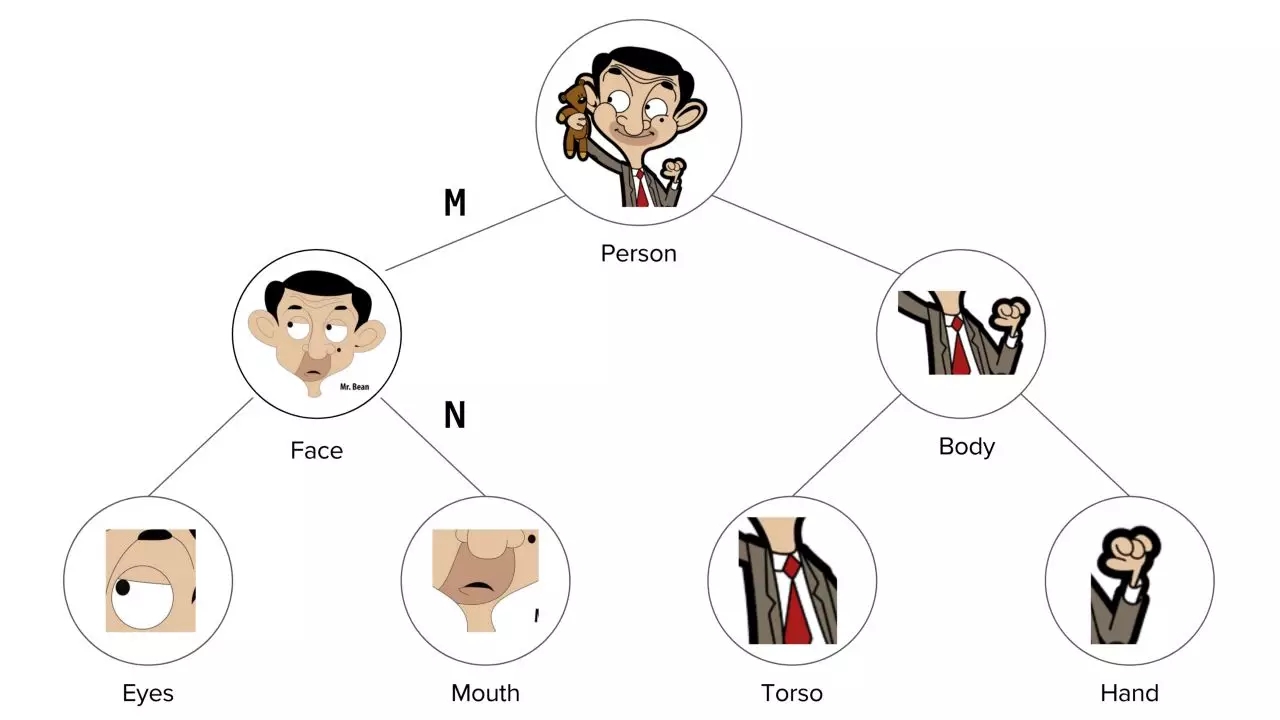
整體是由它的各個(gè)部分組成的，如上圖：

人 (整體) 是由臉和身體組成

臉 (整體) 是由眼睛和嘴巴組成

身體 (整體) 是由軀干和手組成

?

每個(gè)部分通過(guò)一個(gè)姿態(tài)矩陣與其主體相關(guān)聯(lián)。如果 M 是臉對(duì)人姿態(tài)矩陣，N 是嘴巴對(duì)臉姿態(tài)矩陣，那么嘴巴對(duì)人的姿態(tài)矩陣為 N" = MN。

現(xiàn)在我們有一個(gè)照相機(jī)，并且我們知道人對(duì)相機(jī)的幀的姿態(tài)矩陣是 P，可以通過(guò)連乘姿態(tài)矩陣來(lái)提取人的每個(gè)部分的所有基本屬性，比如：

臉對(duì)相機(jī)的幀的姿態(tài)矩陣由 M" = PM 給出

嘴對(duì)相機(jī)的幀的姿態(tài)矩陣由 N" = M"N = PMN 給出

姿態(tài)矩陣 P 表示我們可以從相機(jī)看對(duì)象的不同視點(diǎn)。一張臉上所有特征都是一樣的，所有不同的是你看臉的角度。所有其他對(duì)象 (比如身體、嘴巴和手) 的所有視點(diǎn)都可以由 P 得到。

?

現(xiàn)在告訴你左眼的位置，你可以想象臉的位置了吧。同理，你以為可以從嘴的位置估計(jì)臉的位置。如果由左眼和嘴的位置推出臉的位置相符，數(shù)學(xué)上表示為 Ev·E = Mv·M，其中

Ev 是眼睛的位置向量

E 是眼睛對(duì)臉的姿態(tài)矩陣

Mv 是嘴巴的位置向量

M 是嘴巴對(duì)臉的姿態(tài)矩陣

還記得引言中正常的卡戴珊的圖像 (左圖) 嗎？從嘴和左眼推出臉的位置是相似的，因此得出結(jié)論它們屬于同一個(gè)臉。

但是對(duì)于非正常的卡戴珊的圖像 (下左圖)

從嘴位置推出臉在圖像上角 (下右圖)

從左眼位置推出臉在圖像底部 (下右圖)

從嘴和左眼的位置出發(fā)得到的結(jié)論似乎不相符 (disagreement)，因此它們不應(yīng)該被認(rèn)為出現(xiàn)在同一張臉上。只有當(dāng)嘴和左眼處在正確的位置，從它們出發(fā)得到的結(jié)論才會(huì)相符 (agreement)。在這種情況下，我們就會(huì)發(fā)現(xiàn)嘴巴應(yīng)該在兩只眼睛的下面的中間，只有這樣放置的眼睛和嘴巴才是臉部的一部分，而不是僅僅靠一張嘴巴和眼睛來(lái)識(shí)別臉部。

1.2、不變性和共變性

廣義上講，不變性 (invariance) 是表示 (representation) 不隨變換 (transformation) 變化；而同變性(equivariance) 是表示的變換等價(jià)于變換的表示。

從計(jì)算機(jī)視覺(jué)角度上講，不變性指不隨一些變換來(lái)識(shí)別一個(gè)物體，具體變換包括平移 (translation)，旋轉(zhuǎn) (rotation)，視角 (viewpoint)，放縮 (scale) 等，如下圖所示：

不變性通常在物體識(shí)別上是好事，因?yàn)椴还艿裣裨趺雌揭啤?D旋轉(zhuǎn)、3D旋轉(zhuǎn)和放縮，我們都可以識(shí)別出它是雕像。

如果我們的任務(wù)比物體識(shí)別稍微困難一點(diǎn)，比如我想知道雕像平移了多少個(gè)單位，旋轉(zhuǎn)了多少度，放縮了百分之多少，那么不變性遠(yuǎn)遠(yuǎn)不夠，這時(shí)需要的是同變性。

下圖給出不變性和同變性的具體例子

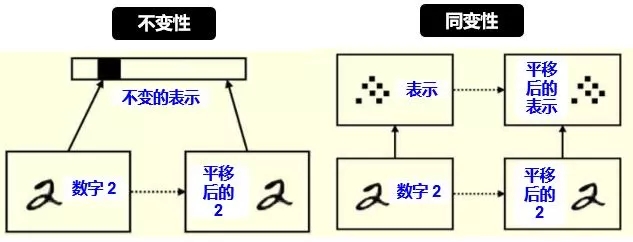
對(duì)平移和旋轉(zhuǎn)的不變性，其實(shí)是丟棄了“坐標(biāo)框架”，而同變性不會(huì)丟失這些信息，它只是對(duì)內(nèi)容的一種變換。具體來(lái)講：

左圖：平移前的 2 和平移后的 2 的表示是一樣的 (比如用 CNN 的池化)，這樣我們只能識(shí)別出 2 ，根本無(wú)法判斷出 2 在圖像中的位置。

右圖：平移前的 2 和平移后的 2 的表示里含有位置這個(gè)信息 (比如用 Capsule)，這樣我們不但能識(shí)別出 2，還能判斷出 2 在圖像中的位置。

1.3、全連接層

在人工神經(jīng)網(wǎng)絡(luò)一貼講的神經(jīng)網(wǎng)絡(luò)每層都是全連接的，也就是說(shuō)上一層每一個(gè)神經(jīng)元都連接到下一層每一個(gè)神經(jīng)元，如下圖所示：

除了偏置項(xiàng)，每層的每一個(gè)神經(jīng)元都連著近鄰層的所有神經(jīng)元，以這種連接關(guān)系的層就叫做全連接層 (fully connected layer, FC layer)，后文簡(jiǎn)稱 FC 層。

如果一個(gè)神經(jīng)網(wǎng)絡(luò)每一層都是全連接的，那么它稱作全連接神經(jīng)網(wǎng)絡(luò) (fully connected neural network, FCNN)，這種 FCNN 不能太深，要不然參數(shù)太多，訓(xùn)練速度太慢。在圖像識(shí)別中，數(shù)據(jù)是高像素彩色照片，它的維度是 324×324×3，第一個(gè) 324 代表高，第二個(gè) 324 代表寬，最后的 3 代表 RGB 三個(gè)顏色維度，乘起來(lái)已經(jīng)有 314928 個(gè)元素了，如果隱藏層有 1024 個(gè)神經(jīng)元，那么總共有 314928×1024 = 3 億多個(gè)參數(shù) (假設(shè)忽略偏置項(xiàng))。這還是一層，如果弄個(gè)十多層，那么訓(xùn)練這么多參數(shù)顯然不現(xiàn)實(shí)，因此在圖像識(shí)別中用的是卷積神經(jīng)網(wǎng)絡(luò)，它有稀疏連接 (sparse connection) 和參數(shù)共享 (parameter sharing) 等特性，會(huì)大大減少需要訓(xùn)練的參數(shù)。

1.4、卷積神經(jīng)網(wǎng)絡(luò)

卷積神經(jīng)網(wǎng)絡(luò) (convolutional neural network,CNN) 的一個(gè)例子如下圖。

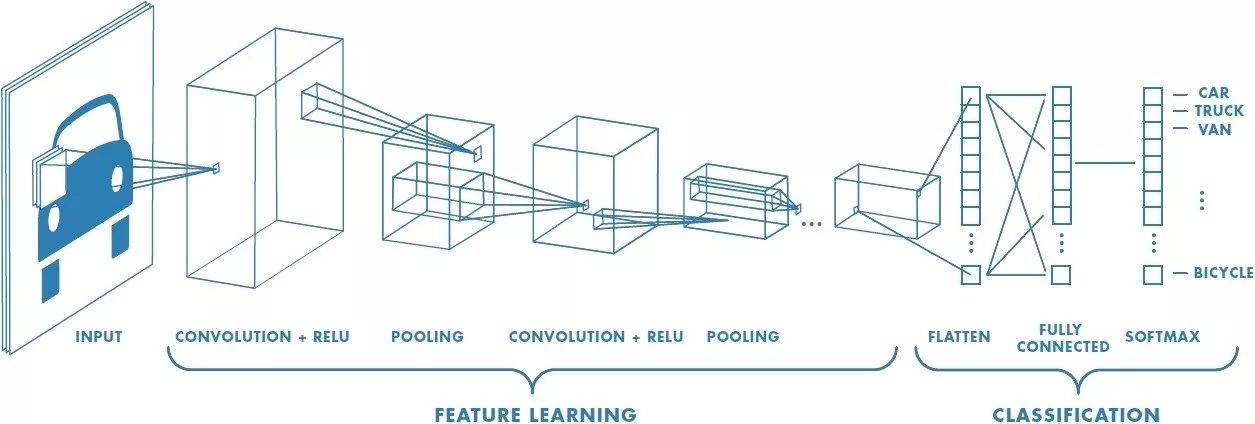
想象給了這張車的圖片，在黑天里你看不到是輛車，你只能用手電筒一點(diǎn)一點(diǎn)掃過(guò)，把每次掃過(guò)看到的東西投影到下一層，以此類推。比如第一層你看到一些橫線豎線斜線，第二層組合成一些圓形方形，第三層組合成輪子車門車身，第四層組合成一輛車。這樣就能用個(gè)手電筒在黑天里辨別出照片里有輛車了。

上面的例子雖然不嚴(yán)謹(jǐn)，但是聽(tīng)起來(lái)很直觀，接下來(lái)給出 CNN 里面的一些定義。

濾波器 (filter)：在輸入數(shù)據(jù)的寬度和高度上滑動(dòng)，與輸入數(shù)據(jù)進(jìn)行卷積，就像上例中的手電筒

卷積 (convolution)：在這里的定義就是把所有“濾波器的像素”乘以“濾波器掃過(guò)圖片的像素”再加總

步長(zhǎng) (stride)：遍歷圖像時(shí)濾波器的步長(zhǎng)，默認(rèn)值為 1，既濾波器每次移動(dòng)一個(gè)像素

填充 (padding)：有時(shí)候會(huì)將輸入數(shù)據(jù)用 0 在邊緣進(jìn)行填充，可以控制輸出數(shù)據(jù)的尺寸 (最常用的是保持輸出數(shù)據(jù)的尺寸與輸入數(shù)據(jù)一致)

千言萬(wàn)語(yǔ)不如兩幅動(dòng)圖 (藍(lán)色是輸入圖片的像素，綠色是濾波器掃過(guò)圖片之后的卷積值)：

第一幅動(dòng)圖將一個(gè) 5x5 的圖像饋送到 3x3 的濾波器。其步長(zhǎng)為 2 (濾波器每2格滑動(dòng))，沒(méi)用填充 (最外層沒(méi)有虛線格)，結(jié)果產(chǎn)生一個(gè)2x2 的圖像。

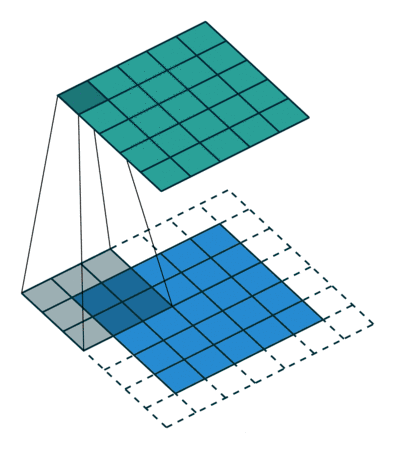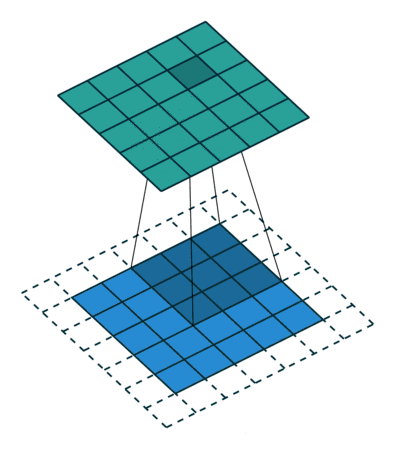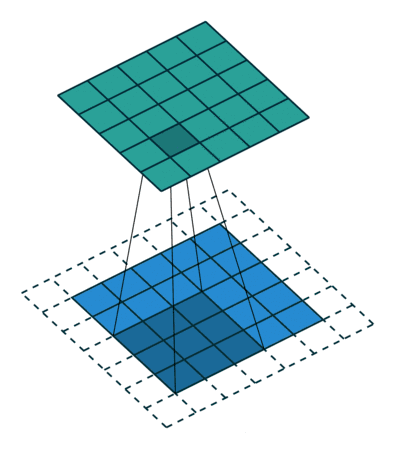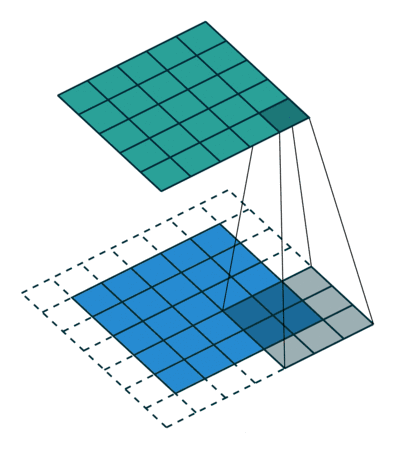
第二幅動(dòng)圖也將一個(gè) 5x5 的圖像饋送到 3x3 的濾波器。其步長(zhǎng)為 1 (濾波器每1格滑動(dòng))，用了 1 層填充(最外層只有一格虛線格)，結(jié)果產(chǎn)生一個(gè) 5x5 的圖像 (加填充可使得輸出和輸入圖像大小不變)。

如果用 nI 代表輸入圖像的大小，f 代表濾波器的大小，s 代表步長(zhǎng)，p 代表填充層數(shù)，nO 代表輸入圖像的大小，那么有 (公式很簡(jiǎn)單就不推導(dǎo)了，大家可以試試上面兩個(gè)例子)

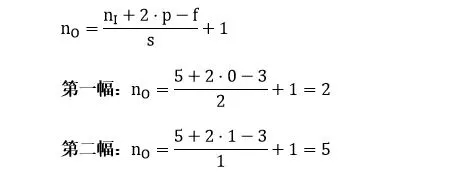
把具體數(shù)字帶進(jìn)來(lái)，大家再捋一遍上面的卷積、濾波器、步長(zhǎng)和填充的概念：

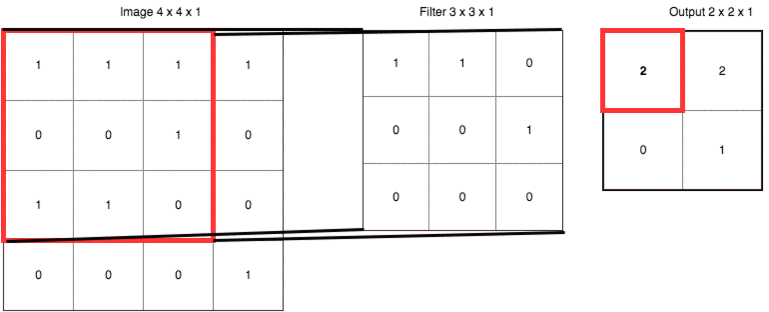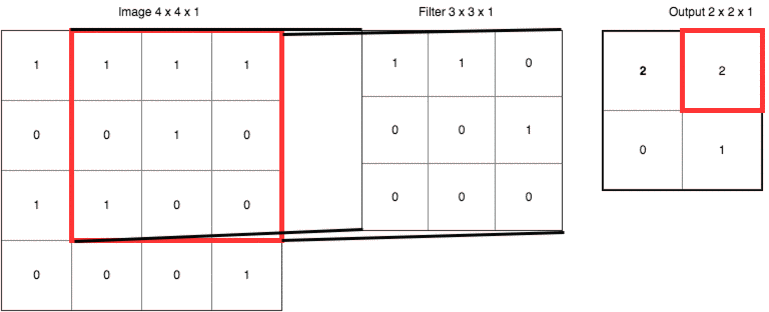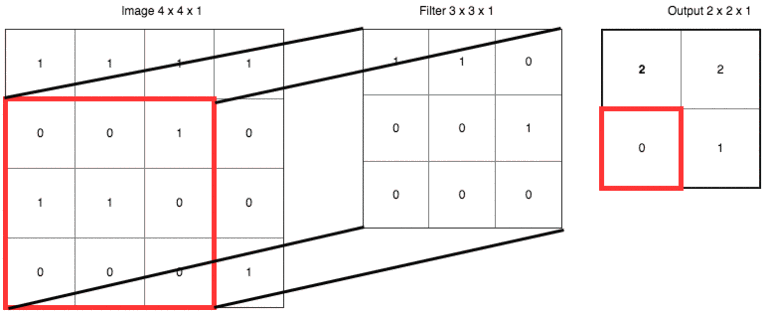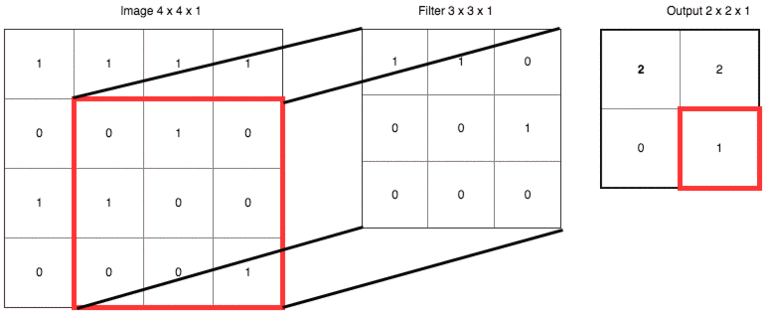
輸出右下角的 1 是這樣卷積來(lái)的：

? ? 0x1 + 1x1 + 0x0?

?+ 1x0 + 0x0 + 0x1

?+ 0x0 + 0x0 + 1x0 = 1 ? ?

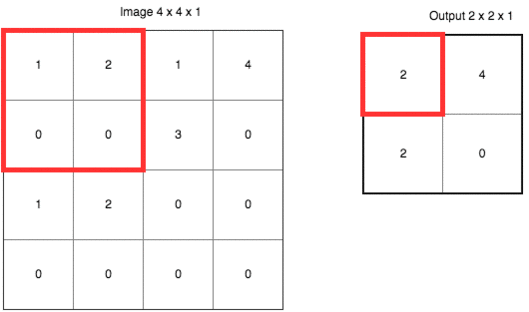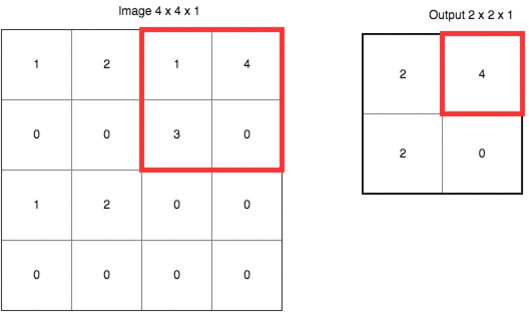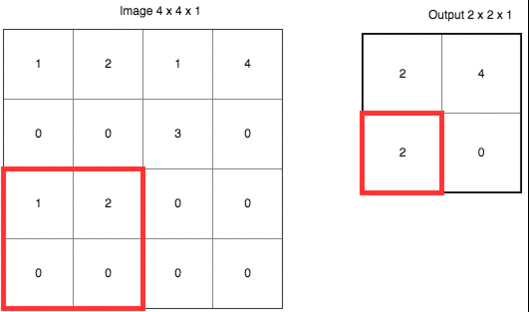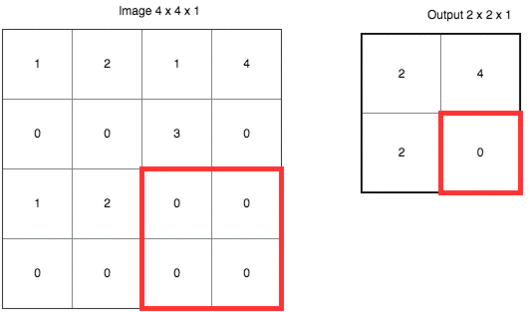
除了上面定義之外，CNN 還有個(gè)很重要的概念叫做池化 (pooling)。它的作用是逐漸降低數(shù)據(jù)體的空間尺寸，這樣的話能減少網(wǎng)絡(luò)中參數(shù)的數(shù)量，使得計(jì)算資源消耗變少，也能有效的控制過(guò)擬合。通常池化使用 max 操作，比如使用尺寸 2x2 的濾波器，以步長(zhǎng)為 2 對(duì)輸入數(shù)據(jù)進(jìn)行降采樣，從 2x2 個(gè)數(shù)字中取較大值。字不如圖，上圖大家慢慢理會(huì)：

雖然池化這項(xiàng)技術(shù)在 CNN 上用的非常好，但是 Hinton 有話要說(shuō)

The pooling operation used in convolutional neuralnetworks is a big mistake and the fact that it works so well is a disaster. -- Hinton

Hinton 認(rèn)為池化在 CNN 的好效果是個(gè)大錯(cuò)誤甚至災(zāi)難。因?yàn)槌鼗瘯?huì)導(dǎo)致重要的信息丟失，如果它是兩層之間的信使，它告訴第二層的是“我們看到左上角有一個(gè)較大值 2，右上角有一個(gè)較大值 4”，但不知道這個(gè) 2 和 4 是從第一層哪里來(lái)的。在引言的例子中，我們知道“兩只眼睛一個(gè)鼻子一張嘴巴”并不代表“一張臉”，要確認(rèn)是張臉，我們還需要知道這些器官之間的相互位置，比如眼睛要在鼻子上方，鼻子要在嘴巴上方，那么才可能是張臉。

2、理論皇

2.1、膠囊定義

膠囊 (Capsule) 是一個(gè)包含多個(gè)神經(jīng)元的載體，每個(gè)神經(jīng)元表示了圖像中出現(xiàn)的特定實(shí)體的各種屬性。這些屬性可以包括許多不同類型的實(shí)例化參數(shù) (instantiation parameter)，例如姿態(tài) (位置、大小、方向)，變形，速度，色相，紋理等。膠囊里一個(gè)非常特殊的屬性是圖像中某個(gè)類別的實(shí)例的存在。它的輸出數(shù)值大小就是實(shí)體存在的概率。

數(shù)學(xué)上常說(shuō)的向量是一個(gè)有方向和長(zhǎng)度的概念，把膠囊類比于數(shù)學(xué)向量，它也有所謂的“長(zhǎng)度”和“方向”。假設(shè)一個(gè)膠囊代表卡戴珊的眼睛，戲稱“卡戴珊眼睛膠囊”，那么其

長(zhǎng)度代表眼睛在圖像某個(gè)位置存在的概率

方向代表眼睛的一些參數(shù)，比如位置，轉(zhuǎn)角，清晰度等等

兩者類比圖如下：

現(xiàn)在大家看膠囊的概念可能還是一頭霧水，我確保你越看到后面思路越清晰，尤其要看小節(jié) 3.1。

2.2、神經(jīng)元類比

為了用詞嚴(yán)謹(jǐn)和類比方便，我們將 Capsule 稱作向量神經(jīng)元 (vector neuron, VN)，而普通的人工神經(jīng)元叫做標(biāo)量神經(jīng)元 (Scalar neuron, SN)，下表總結(jié)了 VN 和 SN 之間的差異：

上表中 VN 里的操作不懂不要緊，接下來(lái)會(huì)一一詳述，本節(jié)只是想從高層面上區(qū)分 VN 和 SN 的區(qū)別，因此大家比較熟悉 SN，從對(duì) SN 的性質(zhì)理解再慢慢過(guò)渡到對(duì) VN 的理解。

?

回想一下人工神經(jīng)網(wǎng)絡(luò)一貼，SN 從其他神經(jīng)元接收輸入標(biāo)量，然后乘以標(biāo)量權(quán)重再求和，然后將這個(gè)總和傳遞給某個(gè)非線性激活函數(shù) (比如 sigmoid, tanh, Relu)，生出一個(gè)輸出標(biāo)量。該標(biāo)量將作為下一層的輸入變量。實(shí)質(zhì)上，SN 可以用以下三個(gè)步驟來(lái)描述：

將輸入標(biāo)量 x 乘上權(quán)重 w

對(duì)加權(quán)的輸入標(biāo)量求和成標(biāo)量 a

用非線性函數(shù)將標(biāo)量 a 轉(zhuǎn)化成標(biāo)量 h

VN 的步驟在 SN 的三個(gè)步驟前加一步：

將輸入向量 u 用矩陣 W 加工成新的輸入向量 U

將輸入向量 U 乘上權(quán)重 c

對(duì)加權(quán)的輸入向量求和成向量 s

用非線性函數(shù)將向量 s 轉(zhuǎn)化成向量 v

VN 和 SN 的過(guò)程總結(jié)如下圖所示：

下一節(jié)來(lái)仔細(xì)研究 VN 的四步工作原理。

2.3、工作原理

為了使問(wèn)題具體化，假設(shè)：

上一層的 VN 代表眼睛 (u1), 鼻子 (u2) 和嘴巴 (u3)，稱為低層特征?

下一層第 j 個(gè)的 VN 代表臉，稱為高層特征。注意下一層可能還有很多別的高層特征，臉是最直觀的一個(gè)

第一步：矩陣轉(zhuǎn)化

公式

根據(jù)小節(jié) 1.1 介紹的姿態(tài)矩陣可知

Uj|1 是根據(jù)眼睛位置來(lái)檢測(cè)臉的位置

Uj|2 是根據(jù)鼻子位置來(lái)檢測(cè)臉的位置

Uj|3 是根據(jù)嘴巴位置來(lái)檢測(cè)臉的位置

現(xiàn)在，直覺(jué)應(yīng)該是這樣的：如果這三個(gè)低層特征 (眼睛，鼻子和嘴) 的預(yù)測(cè)指向相同的臉的位置和狀態(tài)，那么出現(xiàn)在那個(gè)地方的必定是一張臉。如下圖所示：

上左圖預(yù)測(cè)出臉，因?yàn)榧t藍(lán)黃綠圈非常吻合；而上右圖沒(méi)有沒(méi)有預(yù)測(cè)出臉，因?yàn)榧t藍(lán)黃綠圈相差甚遠(yuǎn)。

第二步：輸入加權(quán)

公式

乍一看，這個(gè)步驟和標(biāo)量神經(jīng)元 SN 的加權(quán)形式有點(diǎn)類似。在 SN 的情況下，這些權(quán)重是通過(guò)反向傳播 (backward propagation) 確定的，但是在 VN 的情況下，這些權(quán)重是使用動(dòng)態(tài)路由 (dynamic routing) 確定的，具體算法見(jiàn)小節(jié) 2.4。本節(jié)只從高層面來(lái)解釋動(dòng)態(tài)路由，如下圖：

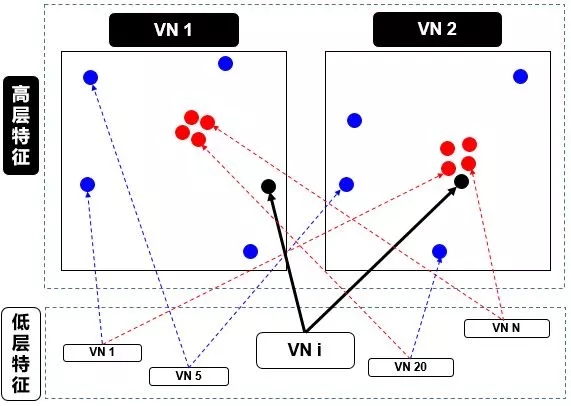
在上圖中，我們有一個(gè)較低級(jí)別 VNi 需要“決定”它將發(fā)送輸出給哪個(gè)更高級(jí)別 VN1 和 VN2。它通過(guò)調(diào)整權(quán)重 ci1 和 ci2 來(lái)做出決定。

現(xiàn)在，高級(jí)別 VN1 和 VN2 已經(jīng)接收到來(lái)自其他低級(jí)別 VN 的許多輸入向量，所有這些輸入都以紅點(diǎn)和藍(lán)點(diǎn)表示。

紅點(diǎn)聚集在一起，意味著低級(jí)別 VN 的預(yù)測(cè)彼此接近

藍(lán)點(diǎn)聚集在一起，意味著低級(jí)別 VN 的預(yù)測(cè)相差很遠(yuǎn)

那么，低別級(jí) VNi 應(yīng)該輸出到高級(jí)別 VN1 還是 VN2？這個(gè)問(wèn)題的答案就是動(dòng)態(tài)路由的本質(zhì)。由上圖看出

VNi 的輸出遠(yuǎn)離高級(jí)別 VN1 中的“正確”預(yù)測(cè)的紅色簇

VNi 的輸出靠近高級(jí)別 VN2 中的“正確”預(yù)測(cè)的紅色簇

而動(dòng)態(tài)路由會(huì)根據(jù)以上結(jié)果產(chǎn)生一種機(jī)制，來(lái)自動(dòng)調(diào)整其權(quán)重，即調(diào)高 VN2 相對(duì)的權(quán)重 ci2，而調(diào)低 VN1 相對(duì)的權(quán)重 ci1。

第三步：加權(quán)求和

公式

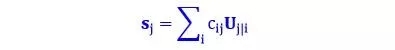
這一步類似于普通的神經(jīng)元的加權(quán)求和步驟，除了總和是向量而不是標(biāo)量。加權(quán)求和的真正含義就是計(jì)算出第二步里面講的紅色簇心 (cluster centroid)。

第四步：非線性激活

公式

這個(gè)公式的確是 VN 的一個(gè)創(chuàng)新，采用向量的新型非線性激活函數(shù)，又叫 squash 函數(shù)，姑且翻譯成“壓縮”函數(shù)。這個(gè)函數(shù)主要功能是使得 vj 的長(zhǎng)度不超過(guò) 1，而且保持 vj 和 sj 同方向。

公式第一項(xiàng)壓扁函數(shù)

如果 sj 很長(zhǎng)，第一項(xiàng)約等于 1

如果 sj 很短，第一項(xiàng)約等于 0

公式第二項(xiàng)單位化向量 sj，因此第二項(xiàng)長(zhǎng)度為 1

這樣一來(lái)，輸出向量 vj 的長(zhǎng)度是在 0 和 1 之間的一個(gè)數(shù)，因此該長(zhǎng)度可以解釋為 VN 具有給定特征的概率。

2.4、動(dòng)態(tài)路由

在小節(jié) 2.3 的第二步已經(jīng)講過(guò)，低級(jí)別 VNi 需要決定如何將其輸出向量發(fā)送到高級(jí)別 VNj，它是通過(guò)改變權(quán)重 cij 而實(shí)現(xiàn)的。首先來(lái)看看 cij 的性質(zhì)：

每個(gè)權(quán)重是一個(gè)非負(fù)值

對(duì)于每個(gè)低級(jí)別 VNi，所有權(quán)重 cij 的總和等于 1

對(duì)于每個(gè)低級(jí)別 VNi，權(quán)重的個(gè)數(shù)等于高級(jí)別 VN 的數(shù)量

權(quán)重由迭代動(dòng)態(tài)路由 (iterative dynamic routing) 算法確定

前兩個(gè)性質(zhì)說(shuō)明 c 符合概率概念。回想一下小節(jié) 2.1，VN 的長(zhǎng)度被解釋為它的存在概率。VN 的方向是其特征的參數(shù)化狀態(tài)。因此，對(duì)于每個(gè)低級(jí)別 VNi，其權(quán)重 cij 定義了屬于每個(gè)高級(jí)別 VNj 的輸出的概率分布。

一言以蔽之，低級(jí)別 VN 會(huì)將其輸出發(fā)送到“同意”該輸出的某個(gè)高級(jí)別 VN。這是動(dòng)態(tài)路由算法的本質(zhì)。很繞口是吧？分析完 Hinton 論文中的動(dòng)態(tài)路由算法就懂了，見(jiàn)截圖：

算法字面解釋如下：

第 1 行：這個(gè)過(guò)程用到的所有輸入 - l 層的輸出 Uj|i，路由迭代次數(shù) r

第 2 行：定義 bij 是 l 層 VNi 應(yīng)該連接 l+1 層 VNj 的可能性，初始值為 0

第 3 行：執(zhí)行第 4-7 行 r 次

第 4 行：對(duì) l 層的 VNi，將 bij 用 softmax 轉(zhuǎn)化成概率 cij

第 5 行：對(duì) l+1 層的 VNj，加權(quán)求和 sj

第 6 行：對(duì) l+1 層的 VNj，壓縮 sj 得到 vj

第 7 行：根據(jù) Uj|i 和 vj 的關(guān)系來(lái)更新 bij

算法邏輯解釋如下：

第 1 行無(wú)需說(shuō)明，要指出的是迭代次數(shù)為 3 次，Hinton 在他論文里這樣說(shuō)道

第 2 行初始化所有 b 為零，這是合理的。因?yàn)閺牡?4 行可看出，只有這樣 c 才是均勻分布的，暗指“l(fā) 層 VN 到底要傳送輸出到 l+1 層哪個(gè) VN 是最不確定的”

第 4 行的 softmax 函數(shù)產(chǎn)出是非負(fù)數(shù)而且總和為 1，致使 c 是一組概率變量

第 5 行的 sj 就是小節(jié) 2.3 第二步里面講的紅色簇心，可以認(rèn)為是低層所有 VN 的“共識(shí)”輸出

第 6 行的 squash 確保向量 sj 的方向不變，但長(zhǎng)度不超過(guò) 1，因?yàn)殚L(zhǎng)度代表 VN 具有給定特征的概率

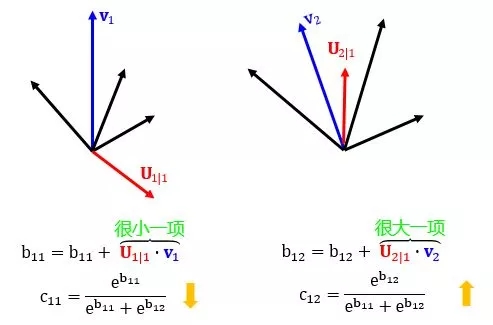
第 7 行是動(dòng)態(tài)路由的精華，用 Uj|i 和 vj 的點(diǎn)積 (dot product) 更新 bij，其中前者是 l 層 VNi 對(duì) l+1 層 VNj 的“個(gè)人”預(yù)測(cè)，而后者是所有 l 層 VN 對(duì) l+1 層 VNj 的“共識(shí)”預(yù)測(cè)：

當(dāng)兩者相似，點(diǎn)積就大，bij 就變大，低層 VNi 連接高層 VNj 的可能性就變大

當(dāng)兩者相異，點(diǎn)積就小，bij 就變小，低層 VNi 連接高層 VNj 的可能性就變小

下面兩幅圖幫助進(jìn)一步理解第 7 行的含義，第一幅講的是點(diǎn)積，論文中用點(diǎn)積來(lái)度量?jī)蓚€(gè)向量的相似性，當(dāng)然還有很多別的度量方式。

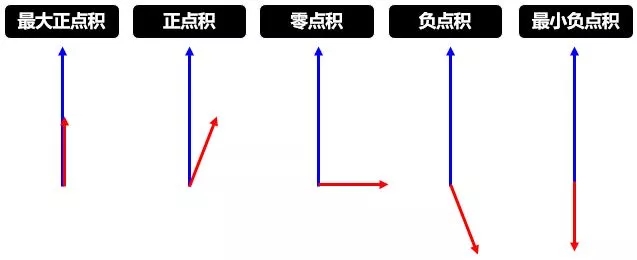
第二幅講的是更新權(quán)重，此消彼長(zhǎng)。

2.5、網(wǎng)絡(luò)結(jié)構(gòu)

本章的前四節(jié)已經(jīng)講明 Capsule 的工作原理和動(dòng)態(tài)路由的邏輯。本節(jié)以 MNIST 數(shù)據(jù)集為例，來(lái)闡明向量神經(jīng)網(wǎng)絡(luò) (capsule network, CapsNet) 的結(jié)構(gòu)和工作原理。

MNIST 全稱為 Modified National Institute of Standards and Technology，其中訓(xùn)練集由來(lái)自 250 個(gè)不同人手寫的數(shù)字構(gòu)成，其中 50% 是高中學(xué)生，50% 來(lái)自人口普查局的工作人員，總共 60000 個(gè)數(shù)字；而測(cè)試集也是同樣比例的手寫數(shù)字?jǐn)?shù)據(jù)，總共 10000 個(gè)數(shù)字。每幅圖像為一個(gè) 28x28 像素的單元，下圖給出 MNIST 里面 0-9 的一些示例。

CapsNet 的輸入輸出和 CNN 是一樣的：

輸入都是 28x28 的二維矩陣

輸出都是 10x1 的概率向量

但 CapsNet 和業(yè)界較先進(jìn)的 CNN 相比，是一個(gè)非常淺的網(wǎng)絡(luò)，中間只有兩個(gè)卷積 (Conv) 層 (見(jiàn)小節(jié)1.4) 和一個(gè)全連接 (FC) 層 (見(jiàn)小節(jié)1.3)，如下圖所示：

圖像輸入到低級(jí)特征 (Conv1)

?

這一步就是一個(gè)常規(guī)的卷積操作，用了 256 個(gè) stride 為 1 的 9x9 的 filter，得到一個(gè) 20x20x256 的輸出。按照原文的意思，這一步主要作用就是對(duì)圖像像素做一次局部特征檢測(cè)。讓我們 Conv1 層的維度是如何得到的。

但為什么不一開(kāi)始就用 Capsule 呢？因?yàn)?Capsule 是用來(lái)表征某個(gè)物體的“實(shí)例”，因此它更適合于表征高級(jí)的實(shí)例。如果直接用 Capsule 吸取圖片的低級(jí)特征內(nèi)容，不是很理想，而 CNN 卻擅長(zhǎng)抽取低級(jí)特征，因此一開(kāi)始用 CNN 是合理的。

低級(jí)特征到 Primary Capsule (Conv2)

Conv2 層才是開(kāi)始含有 Capsule。如果按照普通 CNN 里面的做法，用了 32 個(gè) stride 為 2 的 9x9x256 的 filter，也只能得到 6x6x32 的輸出，算法如下：

但是從上圖和 Hinton 的論文發(fā)現(xiàn)，Conv2 層的維度是 6x6x8x32。這個(gè) 8 怎么來(lái)的？它又代表著什么含義？個(gè)人理解是用 32 個(gè) stride 為 2 的 9x9x256 的filter做了 8 次卷積操作，而且

在 CNN 中，維度為 6x6x1x32 的層里有 6x6x32 元素，每個(gè)元素是一個(gè)標(biāo)量

在 Capsule 中，維度為 6x6x8x32 的層里有 6x6x32 元素，每個(gè)元素是一個(gè) 1x8的向量，既 capsule

Conv2 層的輸出在論文中稱為 Primary Capsule，簡(jiǎn)稱 PrimaryCaps，主要儲(chǔ)存低級(jí)別特征的向量。

Primary Capsule 到 Digit Capsule (FC)

下一層就是存儲(chǔ)高級(jí)別特征的向量，在本例中就是數(shù)字，F(xiàn)C 層的輸出在論文中稱為 Digit Capsule，簡(jiǎn)稱 DigitCaps。PrimaryCaps 和 DigitCaps 是全連接的，但不是像傳統(tǒng)神經(jīng)網(wǎng)絡(luò)標(biāo)量和標(biāo)量相連，而是向量與向量相連。

PrimaryCaps 里面有 6x6x32 元素，每個(gè)元素是一個(gè) 1x8 的向量，而 DigitCaps 有 10 個(gè)元素 (因?yàn)橛?10 個(gè)數(shù)字)，每個(gè)元素是一個(gè) 1x16 的向量。為了讓 1x8 向量與 1x16 向量全連接，需要 6x6x32 個(gè) 8x16 的矩陣 (姿態(tài)矩陣還記得嗎)。

現(xiàn)在 PrimaryCaps 有 6x6x32 = 1152 個(gè) VN，而 DigitCaps 有 10 個(gè) VN，那么 I= 1,2, …, 1152, j = 0,1, …, 9。再用小節(jié) 2.4 講的動(dòng)態(tài)路由算法迭代 3 次計(jì)算 cij 并輸出 10 個(gè) vj。

Digit Capsule 到最終輸出

根據(jù) Capsule 定義，它的長(zhǎng)度表示其表征的內(nèi)容出現(xiàn)的概率，所以做分類時(shí)取輸出向量的 L2 范數(shù) (也就是長(zhǎng)度) 即可。需要注意的是，最后 Capsule 輸出的概率總和并不等于 1，也就是 Capsule 有同時(shí)識(shí)別多個(gè)物體的能力。

損失函數(shù)

由于 Capsule 允許多個(gè)分類同時(shí)存在，所以不能直接用傳統(tǒng)的交叉熵 (cross-entropy) 損失，一種替代方案是用間隔損失 (margin loss)

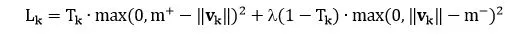
其中

k 是分類

Tk 是分類的指示函數(shù) (k 類存在為 1，不存在為 0)

m+ 為上界，懲罰假陽(yáng)性 (false positive) ，即預(yù)測(cè) k 類存在但真實(shí)不存在，識(shí)別出來(lái)但錯(cuò)了

m- 為下界，懲罰假陰性 (false negative) ，即預(yù)測(cè) k 類不存在但真實(shí)存在，沒(méi)識(shí)別出來(lái)

λ 是比例系數(shù)，調(diào)整兩者比重

總的損失是各個(gè)樣例損失之和。論文中 m+ = 0.9, m- = 0.1, λ = 0.5，用大白話說(shuō)就是

如果 k 類存在，||vk|| 不會(huì)小于 0.9

如果 k 類不存在，||vk|| 不會(huì)大于 0.1

懲罰假陽(yáng)性的重要性大概是懲罰假陰性的重要性的 2 倍

重構(gòu)表示

魯棒性強(qiáng)的模型一定有重構(gòu)的能力。如果模型能夠重構(gòu)，證明它至少有了一個(gè)好的表示，并且從重構(gòu)結(jié)果中可以看出模型存在的問(wèn)題。

?

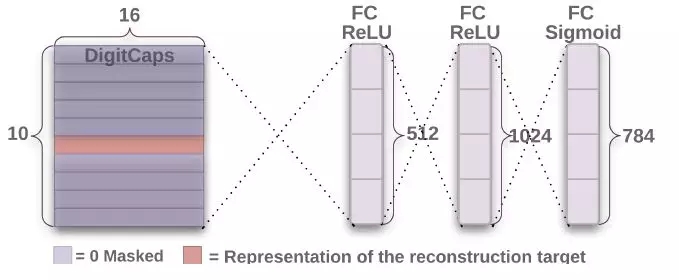
重構(gòu)的時(shí)候，我們多帶帶取出 (上圖橘色) 需要重構(gòu)的向量，扔到后面的 3 層全連接網(wǎng)絡(luò)中重構(gòu)。注意最終輸出的維度是 784 = 28×28，正好是最初圖像輸入的維度。

重構(gòu)損失 (reconstruction loss) 就是把最終輸出和最初輸入的 784 個(gè)單元上的像素值相減并平方求和。總體損失 (total loss) 就是

總體損失 = 間隔損失 + α·重構(gòu)損失

其中 α = 0.005，間隔損失還是占主導(dǎo)地位。

3、實(shí)踐狼

3.1、帆船房子

本節(jié)用一個(gè)具體的“三角形長(zhǎng)方形組成帆船房子”的例子來(lái)直觀解釋第 2 章的理論知識(shí)和重要概念，假設(shè)“低層 Capsule”里面有三角形和長(zhǎng)方形，而“高層 Capsule”里面有帆船和房子。為了解釋方便，定義：

三角形 VN：低層 Capsule 的三角形

長(zhǎng)方形 VN：低層 Capsule 的長(zhǎng)方形

帆船 VN：高層 Capsule 的帆船

房子 VN：高層 Capsule 的房子

正向作圖和反向作圖

如上圖所示，計(jì)算機(jī)作圖 (computer graphics) ，通常認(rèn)為是正向作圖，是根據(jù)各個(gè)物體的參數(shù)，比如中心橫坐標(biāo) x，中心縱坐標(biāo) y 和旋轉(zhuǎn)角度，在屏幕中打出 (rendering) 帆船的圖像。而反向作圖 (inverse graphics) 是根據(jù)屏幕中帆船的圖像，反推出各個(gè)物體的參數(shù)。

想知道上圖三角形的 -65 度和長(zhǎng)方形的 16 度怎么來(lái)的，見(jiàn)下圖解釋。

向量神經(jīng)元做的事就是反向作圖。

向量神經(jīng)元性質(zhì)

假設(shè)藍(lán)箭頭代表三角形，黑箭頭代表長(zhǎng)方形：

藍(lán)箭頭的長(zhǎng)度表示三角形出現(xiàn)的概率大小

黑箭頭的長(zhǎng)度表示長(zhǎng)方形出現(xiàn)的概率大小

藍(lán)箭頭的方向表示三角形的姿態(tài)參數(shù) (這里指朝向)

黑箭頭的方向表示長(zhǎng)方形的姿態(tài)參數(shù) (這里指朝向)

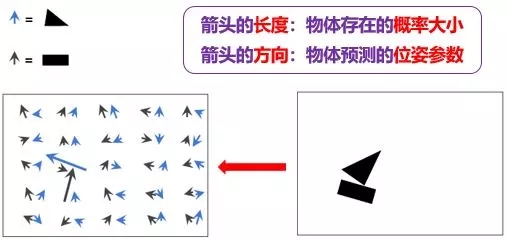
由上圖左邊明顯看出

有一個(gè)藍(lán)箭頭和一個(gè)黑箭頭非常大，說(shuō)明在上圖右邊各自相應(yīng)位置上存在的三角形和長(zhǎng)方形的可能性非常大

其他地方的所有藍(lán)箭頭和黑箭頭非常小，說(shuō)明在上圖右邊那些位置上存在的三角形和長(zhǎng)方形的可能性非常小

根據(jù)藍(lán)箭頭的方向，我們大概知道三角形逆時(shí)針轉(zhuǎn)了 65 度

根據(jù)黑箭頭的方向，我們大概知道長(zhǎng)方形順時(shí)針轉(zhuǎn)了 16 度

?

同變性

CNN 的池化只能帶來(lái)“不變性 (invariance)”，只能識(shí)別下面兩圖中都有帆船，但我們不想只追求識(shí)別率，我們想要的更多，比如 VN 帶來(lái)的“同變性 (equivariance)”，不但能識(shí)別兩圖中有帆船，還能看出它們的傾斜度不同。

從上圖看出，當(dāng)帆船旋轉(zhuǎn)了一些角度，它包含的三角形和長(zhǎng)方形也旋轉(zhuǎn)了一些角度，而對(duì)應(yīng)的藍(lán)箭頭和黑箭頭也旋轉(zhuǎn)了一些角度。三角形和長(zhǎng)方形是低層物體，帆船是高層物體，物體與物體之間是有層次 (hierarchy) 的。當(dāng)高層物體轉(zhuǎn)動(dòng)時(shí)，它包含的所有低層物體也隨之轉(zhuǎn)動(dòng)。

?

物體層次

三角形和長(zhǎng)方形可以組成帆船，也可以組成房子。

如果把帆船和房子當(dāng)成一個(gè)整體的話 (忽略其組成成分三角形和長(zhǎng)方形)，那么它們也有自己的 x-y 坐標(biāo)和角度，如圖所示，帆船沿順時(shí)針?lè)较蛐D(zhuǎn)了 16 度，房子沿逆時(shí)針?lè)较蛐D(zhuǎn)了 5 度。

現(xiàn)在問(wèn)題是，如果我們識(shí)別出圖片上有三角形和長(zhǎng)方形，那么它們組合的是房子還是帆船？

預(yù)測(cè)物體

下圖勾畫(huà)出由“低層 VN 代表的三角形和長(zhǎng)方形”來(lái)預(yù)測(cè)“高層 VN 代表的房子和帆船”的來(lái)龍去脈。

如果根據(jù)長(zhǎng)方形的姿態(tài)開(kāi)始預(yù)測(cè)，則房子和帆船的姿態(tài)如左圖所示。注意房子和帆船里的長(zhǎng)方形朝向和位置完全相同。

如果根據(jù)三角形的姿態(tài)開(kāi)始預(yù)測(cè)，則房子和帆船的姿態(tài)如右圖所示。注意房子和帆船里的三角形朝向和位置完全相同。

淺談路由

路由 (routing) 就是通過(guò)互聯(lián)網(wǎng)絡(luò)把信息從源地址傳輸?shù)侥康牡刂返幕顒?dòng)，而這里路由指的是通過(guò)神經(jīng)網(wǎng)絡(luò)把信息從低層 VN 傳輸?shù)礁邔?VN 的活動(dòng)。

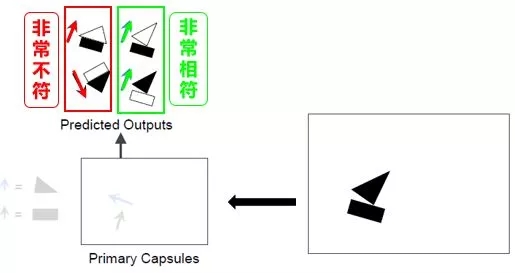
“三角形和長(zhǎng)方形的 VN”路由出來(lái)的“帆船 VN”看起來(lái)非常相似，而它們路由出來(lái)的“房子 VN”看來(lái)一點(diǎn)也不像。因此我們有信心的認(rèn)為圖像里存在就是一艘帆船而不是一棟房子。

動(dòng)態(tài)路由

動(dòng)態(tài)路由 (dynamic routing) 是找到每一個(gè)“低層 VN”的輸出最有可能貢獻(xiàn)給哪個(gè)“高層 VN”。具體到我們的實(shí)例，就是找到“三角形或長(zhǎng)方形”最有可能組成“房子或帆船”。

用 i 代表低層 VN 中長(zhǎng)方形或三角形的索引 (本例中 i = 1, 2)，用 j 代表高層 VN 中房子或帆船的索引 (本例中 j = 1, 2)，定義

bij = 低層 VNi 連接高層 VNj 的可能性，初始值為 0

cij = 低層 VNi 連接高層 VNj 的概率，總和為 1

bi = 低層 VNi 連接所有高層 VNj 的可能性，初始值為 0

ci = 低層 VNi 連接所有高層 VNj 的概率

Uj|i = 由低層 VNi 預(yù)測(cè)的高層 VNj?

cij 是 bij 做 softmax 之后的結(jié)果，因此初始值 0.5 (j 層只有 2 個(gè) VN)。

為了達(dá)到以上目的，動(dòng)態(tài)路由在每個(gè)回合都干了“歸一、預(yù)測(cè)、加總、壓縮和更新”這五件事，然后重復(fù)若干回合：

對(duì)長(zhǎng)方形 (i=1) 和三角形 (i=2)

歸一：

計(jì)算概率 (c11, c12) = 歸一(b11, b12)

計(jì)算概率 (c21, c22) = 歸一(b21, b22)

預(yù)測(cè)：

從長(zhǎng)方形到房子 U1|1 和小船 U2|1

從三角形到房子 U1|2 和小船 U2|2

加總：

房子的綜合預(yù)測(cè) s1 = c11U1|1 + c21U1|2

帆船的綜合預(yù)測(cè) s2 = c12U2|1 + c22U2|2

壓縮：

單位化房子的綜合預(yù)測(cè) v1 = 壓縮(s1)

單位化帆船的綜合預(yù)測(cè) v2 = 壓縮(s2)

更新：

b11 = b11 + 相似度(U1|1, v1)

b12 = b12 + 相似度(U2|1, v2)

b21 = b21 + 相似度(U1|2, v1)

b22 = b22 + 相似度(U2|2, v2)

其中歸一函數(shù)是 softmax 函數(shù)，壓縮函數(shù)是 squash 函數(shù)，相似度函數(shù)是 dot product。下面接著用實(shí)例來(lái)解釋上述步驟。

初始化概率和參數(shù)：

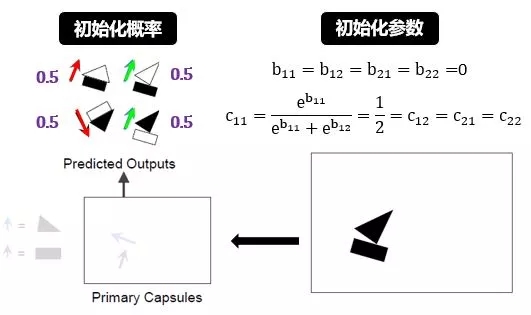
初始化所有 b 為零，根據(jù) softmax 函數(shù)計(jì)算出所有 c 都是 0.5。該初始化是符合直覺(jué)的，一開(kāi)始“三角形或長(zhǎng)方形到底是帆船還是房子的一部分”這樣一個(gè)判斷是最不確定的，而 50% 的概率對(duì)應(yīng)著這種最不確定情景。

預(yù)測(cè)-加總-壓縮：

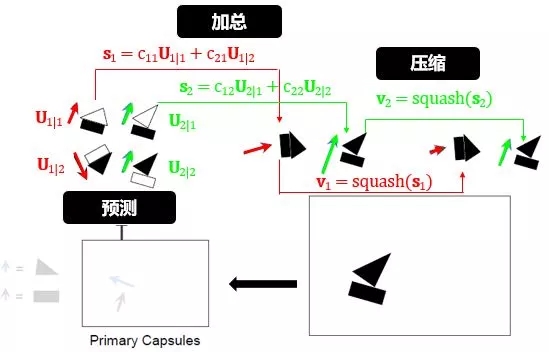
預(yù)測(cè)就是用姿態(tài)矩陣做了轉(zhuǎn)化 (見(jiàn)小節(jié) 1.1)，分別由長(zhǎng)方形和三角形的位置預(yù)測(cè)了房子/帆船的位置：

加總就是分別將房子/帆船的預(yù)測(cè)位置求個(gè)加權(quán)總和，可以理解成房子/帆船的平均位置：

壓縮就是單位化位置向量：

更新參數(shù)：

參數(shù) b 就是從三角形/長(zhǎng)方形推出房子/帆船的可能性，如圖：

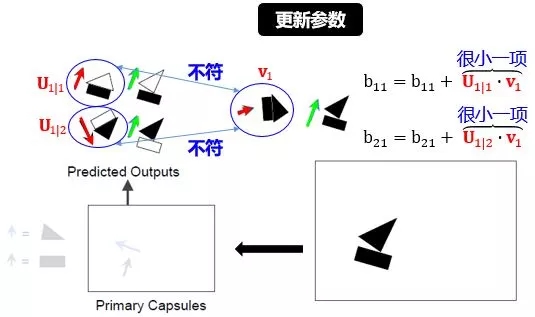
上圖已解釋的很清楚，核心思想就是

?

當(dāng)兩個(gè)物體相似時(shí)，它們的點(diǎn)積比較大，從而增大可能性

當(dāng)兩個(gè)物體相異時(shí)，它們的點(diǎn)積比較小，從而減小可能性

最后用 softmax 更新概率 cij

重復(fù)以上預(yù)測(cè)-加總-壓縮的步驟，循環(huán) r 次結(jié)束。

最后用以下規(guī)則來(lái)判斷到底從低層 VN 路由到高層 VN：

如果 b11 > b12 則 c11 > c12，那么三角形路由到房子概率大，反之路由到帆船概率大

如果 b21 > b22 則 c21 > c22，那么長(zhǎng)方形路由到房子概率大，反之路由到帆船概率大

3.2、代碼解析

基本引入包和設(shè)置

# Import useful packages

import numpy as np

import tensorflow as tf

%matplotlib inline

import matplotlib.pyplot as plt

# Reset the default graph for rerun notebook

tf.reset_default_graph()

# Reset the random seed for reproducibility

np.random.seed(42)

tf.set_random_seed(42)

讀取 MNIST 數(shù)據(jù)

from tensorflow.examples.tutorials.mnist import input_data

mnist = input_data.read_data_sets("/tmp/data/")

n_samples = 5

plt.figure(figsize=(n_samples * 2, 3))

for index in range(n_samples):

? ?plt.subplot(1, n_samples, index + 1)

? ?sample_image = mnist.train.images[index].reshape(28, 28)

? ?plt.imshow(sample_image, cmap="binary")

? ?plt.axis("off")

plt.show()

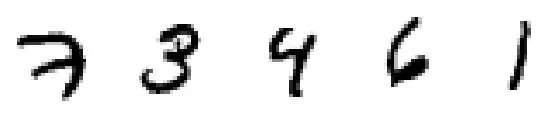
從 tensorflow 數(shù)據(jù)庫(kù)里引進(jìn) MNSIT 數(shù)據(jù)，選出 5 個(gè)樣本打印出來(lái)。

特征 X 和標(biāo)簽 y

X = tf.placeholder(shape=[None, 28, 28, 1], dtype=tf.float32, name="X")

y = tf.placeholder(shape=[None], dtype=tf.int64, name="y")

定義特征 X 和標(biāo)簽 y，placeholder 是占位符的意思，用于創(chuàng)建占位，當(dāng)需要時(shí)再將真正的數(shù)據(jù)傳入進(jìn)去，即利用 feed_dict 的字典結(jié)構(gòu)給 placeholder 變量“喂數(shù)據(jù)”。Placeholder 有三個(gè)參數(shù)：

數(shù)據(jù)維數(shù)

數(shù)據(jù)類型

數(shù)據(jù)命名

X 有四維，分別是圖片個(gè)數(shù)，寬度像素，高度像素，色彩維度。

圖片個(gè)數(shù)在定義占位符時(shí)不知道，只有在喂數(shù)據(jù)時(shí)才知道，因此用 None

圖片都包含 28x28 像素，每個(gè)像素用 float32 類型表示

圖片是黑白的，沒(méi)有 RGB，因此維度是 1

y 只有一維，就是圖片個(gè)數(shù)。其標(biāo)簽值就是用 0 到 9 的 int64 類型表示。

卷積層

conv1_params = {

? ?"filters": 256,

? ?"kernel_size": 9,

? ?"strides": 1,

? ?"padding": "valid",

? ?"activation": tf.nn.relu,

}

conv1 = tf.layers.conv2d(X, name="conv1", **conv1_params)

首先在字典 conv1_params 里定義卷積層的參數(shù)，濾波器個(gè)數(shù) 256、濾波器大小 9、步長(zhǎng) 1，填充 valid 指的沒(méi)有填充、激活函數(shù)用的 relu。然后用 tensorflow 里的函數(shù) conv2d 建立 conv1，其中 ** 代表傳遞一個(gè)字典類型的變量。最終 conv1 的 shape 是 [?, 20, 20, 256]，其中 ? 代表之后才確定的圖片個(gè)數(shù)。

Primary Capsules

caps1_n_maps = 32

caps1_n_dims = 8

conv2_params = {

? ?"filters": caps1_n_maps * caps1_n_dims,

? ?"kernel_size": 9,

? ?"strides": 2,

? ?"padding": "valid",

? ?"activation": tf.nn.relu

}

conv2 = tf.layers.conv2d(conv1, name="conv2", **conv2_params)

建立 conv2 和 conv1 是一樣的，conv2 的 shape 是 [?, 6, 6, 256]。這里 256 其實(shí)是 32 和 8 的乘積，由小節(jié) 2.5 可知，該層實(shí)際用了 32 個(gè)濾波器濾了 8 遍。

更需要注意的是，該層 (PrimaryCaps) 每個(gè) Capsule (1x8 向量) 和下層 ?(DigitCaps) 每個(gè) Capsule (1x16 向量) 全連接，那么較好生成一個(gè)變量含有 1152 個(gè) Capsule，因此將 conv2 的 shape 轉(zhuǎn)成 [?, 1152, 8] (總元素和 6x6x256 一樣多)，該變量記做 caps1_raw, 見(jiàn)下圖代碼。

caps1_n_caps = caps1_n_maps * 6 * 6

caps1_raw = tf.reshape(conv2, [-1, caps1_n_caps, caps1_n_dims],

? ? ? ? ? ? ? ? ? ? ?name="caps1_raw")

Reshape 函數(shù)里面 -1 指的是某個(gè)維度大小，使得變換維度后的變量和變換前的變量的總元素個(gè)數(shù)不變。比如 A 原來(lái)的 shape 是 [3, 2, 3]，如果 B 用

reshape(A, [-1,9])，則 B.shape = [2,9]

reshape(A, [9,-1])，則 B.shape = [9,2]

reshape(A, [2,-1,3])，則 B.shape = [2,3,3]

定義壓縮函數(shù) squash

def squash(s, axis=-1, epsilon=1e-7, name=None):

? ?with tf.name_scope(name, default_name="squash"):

? ? ? ?squared_norm = tf.reduce_sum(tf.square(s), axis=axis,

? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? keep_dims=True)

? ? ? ?safe_norm = tf.sqrt(squared_norm + epsilon)

? ? ? ?squash_factor = squared_norm / (1. + squared_norm)

? ? ? ?unit_vector = s / safe_norm

? ? ? ?return squash_factor * unit_vector

這里有個(gè)技巧，在分母 ||s|| 里面加入小量10-7，防止分母為零。最后用 squash 函數(shù)將 caps1_raw 單位化得到 cap1_output。它的 shape 也是 [?, 1152, 8]。

caps1_output = squash(caps1_raw, name="caps1_output")

Digit Capsules

根據(jù)小節(jié) 2.3，1152 個(gè) PrimaryCaps 的變量 (1x8) 需要乘以姿態(tài)矩陣 (8x16) 得到 10 個(gè) DigitCaps 的變量 (1x16)。下面設(shè)計(jì)的高維矩陣相乘是一種較高效的做法。

其中

第一個(gè)數(shù)組的 shape 是 [1152, 10, 16, 8]

第二個(gè)數(shù)組的 shape 是 [1152, 10, 8, 1]

第三個(gè)數(shù)組的 shape 是 [1152, 10, 16, 1]

上面數(shù)組已經(jīng)是四維了，但別忘了還有圖片個(gè)數(shù)這一維，需要用 tensorflow 里面的 tile 函數(shù)來(lái)增加一維。見(jiàn)下面三塊代碼：

數(shù)組 W

caps2_n_caps = 10

caps2_n_dims = 16

init_sigma = 0.01

W_init = tf.random_normal(

? ?shape=(1, caps1_n_caps, caps2_n_caps, caps2_n_dims, caps1_n_dims),

? ?stddev=init_sigma, dtype=tf.float32, name="W_init")

W = tf.Variable(W_init, name="W")

batch_size = tf.shape(X)[0]

W_tiled = tf.tile(W, [batch_size, 1, 1, 1, 1], name="W_tiled")

首先定義一個(gè)四維隨機(jī)變量 W_init，當(dāng) W 的初始值，它的 shape 是 [1152, 10, 16, 8]，batch_size 是一批圖片的個(gè)數(shù)。tile 函數(shù)實(shí)際就是將 W 復(fù)制了batch_size個(gè)，儲(chǔ)存在 W_tiled，它的 shape 是 [?, 1152, 10,16, 8]，如下圖：

數(shù)組 u

caps1_output_expanded = tf.expand_dims(caps1_output, -1,

? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?name="caps1_output_expanded")

caps1_output_tile = tf.expand_dims(caps1_output_expanded, 2,

? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?name="caps1_output_tile")

caps1_output_tiled = tf.tile(caps1_output_tile, [1, 1, caps2_n_caps, 1, 1],

? ? ? ? ? ? ? ? ? ? ? ? ? ?name="caps1_output_tiled")

這一步是最讓人困惑的。

首先看最終想要的結(jié)果的 shape 是 [?, 1152, 10, 8, 1]，而 caps1_output 的 shape 是 [?, 1152, 8]

需要在最后的 axis 上擴(kuò)張一維，用 expand_dims 函數(shù)和參數(shù) -1，得到 caps1_output_expanded 的 shape 是 [?, 1152, 8, 1]

需要在第二個(gè) axis 上擴(kuò)張一維，用 expand_dims 函數(shù)和參數(shù) 2，得到 caps1_output_tile 的 shape 是 [?, 1152, 1, 8, 1]

用 tile 函數(shù)將第三個(gè) axis 上復(fù)制 10 個(gè)，得到 caps1_output_tiled 的 shape 是 [?, 1152, 10, 8, 1]

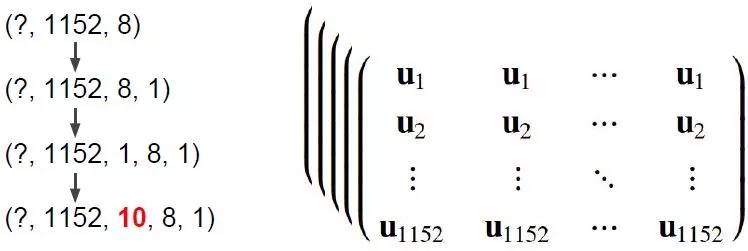
數(shù)組 u_hat

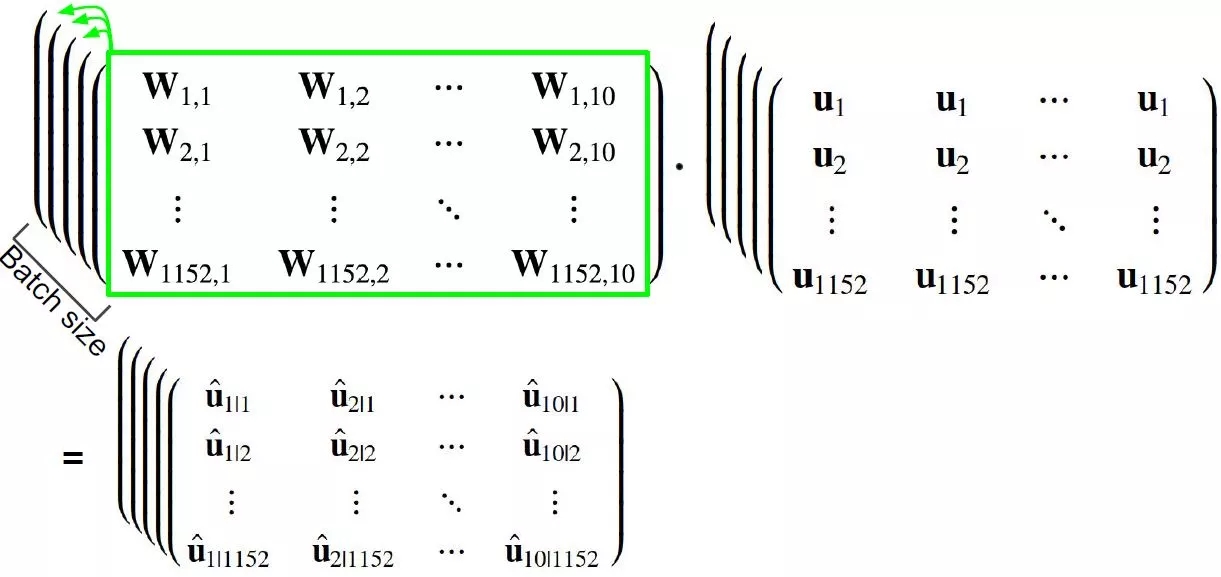
caps2_predicted = tf.matmul(W_tiled, caps1_output_tiled,

? ? ? ? ? ? ? ? ? ? ? ? ? ?name="caps2_predicted")

函數(shù) matmul 是將高維數(shù)組中每個(gè)矩陣元素相乘

用 shape 為 [?, 1152, 10, 16, 8] 的 W_tiled

乘以 shape 為 [?, 1152, 10, 8, 1] 的 caps1_output_tiled

等于 shape 為 [?, 1152, 10, 16, 1] 的 caps2_predicted

如下圖所示：

動(dòng)態(tài)路由

第一輪初始化 b

b = tf.zeros([batch_size, caps1_n_caps, caps2_n_caps, 1, 1],

? ? ? ? ? ? dtype=np.float32, name="raw_weights")

b 的 shape 為 [?, 1152, 10, 1, 1]。

第一輪初始化 c

c = tf.nn.softmax(raw_weights, dim=2, name="routing_weights")

c 的 shape 為 [?, 1152, 10, 1, 1]，而且在第二個(gè) axis 上做歸一化，原因就是每一個(gè) caps1 到所有 caps2 的概率總和為一。

第一輪計(jì)算 s 和 v

weighted_predictions = tf.multiply(c, caps2_predicted,

? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?name="weighted_predictions")

s = tf.reduce_sum(weighted_predictions, axis=1,?

? ? ? ? ? ? ? ? ?keep_dims=True, name="weighted_sum")

v = squash(s, axis=-2, name="caps2_output_round_1")

weighted_predictions 的 shape 為 [?, 1152, 10, 16, 1]，而 s 和 v 的 shape 為 [?, 1, 10, 16, 1]，因?yàn)樵诘谝粋€(gè) axis 上用 reduce_sum 函數(shù)求和再用 squash 函數(shù)壓縮。

第二輪迭代

v_tiled = tf.tile(v, [1, caps1_n_caps, 1, 1, 1],

? ? ? ? ?name="caps2_output_round_1_tiled")

agreement = tf.matmul(caps2_predicted, v_tiled,

? ? ? ? ? ? ? ? ? ? ?transpose_a=True, name="agreement")

b = tf.add(b, agreement, name="raw_weights_round_2")

c = tf.nn.softmax(b, dim=2, name="routing_weights_round_2")

weighted_predictions = tf.multiply(c, caps2_predicted, ??

? ? ? ? ? ? ? ? ? ? ? name="weighted_predictions_round_2")

s = tf.reduce_sum(weighted_predictions, axis=1,?

? ? ? ? ? ? ? ? ?keep_dims=True, name="weighted_sum_round_2")

v = squash(s, axis=-2, name="caps2_output_round_2")

第三輪迭代

v_tiled = tf.tile(v, [1, caps1_n_caps, 1, 1, 1],

? ? ? ? ?name="caps2_output_round_2_tiled")

agreement = tf.matmul(caps2_predicted, v_tiled,

? ? ? ? ? ? ? ? ? ? ?transpose_a=True, name="agreement")

b = tf.add(b, agreement, name="raw_weights_round_3")

c = tf.nn.softmax(b, dim=2, name="routing_weights_round_3")

weighted_predictions = tf.multiply(c, caps2_predicted, ??

? ? ? ? ? ? ? ? ? ? ? name="weighted_predictions_round_3")

s = tf.reduce_sum(weighted_predictions, axis=1,?

? ? ? ? ? ? ? ? ?keep_dims=True, name="weighted_sum_round_3")

v = squash(s, axis=-2, name="caps2_output_round_3")

上面這種寫出每一輪迭代的方法有點(diǎn)低效，一種替代方法可以用 for 語(yǔ)句，但是它是靜態(tài)循環(huán) (static loop), 在 tensorflow 里面每定義一次操作都會(huì)增大內(nèi)部的流程圖。這里三次迭代沒(méi)問(wèn)題，如果很多的建議用 tf.while_loop() 函數(shù)，這個(gè)是動(dòng)態(tài)循環(huán) (dynamic loop)。除了減小流程圖大小以外，動(dòng)態(tài)循環(huán)還能減少 GPU RAM 的使用。

間隔損失

m_plus = 0.9

m_minus = 0.1

lambda_ = 0.5

T = tf.one_hot(y, depth=caps2_n_caps, name="T")

v_norm = tf.norm(v, axis=-2, keep_dims=True, name="caps2_output_norm")

FP_raw = tf.square(tf.maximum(0., m_plus - v_norm), name="FP_raw")

FP = tf.reshape(FP_raw, shape=(-1, 10), name="FP")

FN_raw = tf.square(tf.maximum(0., v_norm - m_minus), name="FN_raw")

FN = tf.reshape(FN_raw, shape=(-1, 10), name="FN")

L = tf.add(T * FP, lambda_ * (1.0 - T) * FN, name="L")

margin_loss = tf.reduce_mean(tf.reduce_sum(L, axis=1), name="margin_loss")

實(shí)現(xiàn)小節(jié) 2.5 里面的公式，用 one_hot 函數(shù)將數(shù)字轉(zhuǎn)換成 0-1 的啞變量矩陣。

Mask 機(jī)制

mask_with_labels = tf.placeholder_with_default(False, shape=(),

? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?name="mask_with_labels")

reconstruction_targets = tf.cond(mask_with_labels, # condition

? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?lambda: y, ? ? ? ?# if True

? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?lambda: y_pred, ? # if False

? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?name="reconstruction_targets")

reconstruction_mask = tf.one_hot(reconstruction_targets,

? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?depth=caps2_n_caps,

? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?name="reconstruction_mask")

reconstruction_mask_reshaped = tf.reshape(

? reconstruction_mask, [-1, 1, caps2_n_caps, 1, 1],

? name="reconstruction_mask_reshaped")

caps2_output_masked = tf.multiply(

? v, reconstruction_mask_reshaped,

? name="caps2_output_masked")

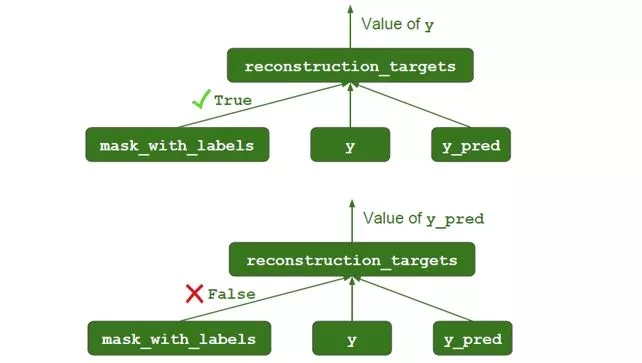
在重構(gòu)中，并不是每一個(gè)數(shù)字的輸出都傳送到解碼器的，只有目標(biāo)數(shù)字的輸出才需要傳送出去，因此需要做一個(gè) one_hot 轉(zhuǎn)換。此外

在訓(xùn)練中，需要傳出的是 y

在測(cè)試中，需要傳出的是 y_pred

解碼器

n_hidden1 = 512

n_hidden2 = 1024

n_output = 28 * 28

decoder_input = tf.reshape(caps2_output_masked,

? ? ? ? ? ? ? ? ? ? ? ? ?[-1, caps2_n_caps * caps2_n_dims],

? ? ? ? ? ? ? ? ? ? ? ? ?name="decoder_input")

with tf.name_scope("decoder"):

? hidden1 = tf.layers.dense(decoder_input, n_hidden1,

? ? ? ? ? ? ? ? ? ? ? ? ? ? activation=tf.nn.relu,

? ? ? ? ? ? ? ? ? ? ? ? ? ? name="hidden1")

? hidden2 = tf.layers.dense(hidden1, n_hidden2,

? ? ? ? ? ? ? ? ? ? ? ? ? ? activation=tf.nn.relu,

? ? ? ? ? ? ? ? ? ? ? ? ? ? name="hidden2")

? decoder_output = tf.layers.dense(hidden2, n_output,

? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?activation=tf.nn.sigmoid,

? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?name="decoder_output")

解碼器由個(gè) 3 全連接層組成，每層大小分別為 512,1024 和 784，用layers.dense 函數(shù)來(lái)構(gòu)建。

重構(gòu)損失

X_flat = tf.reshape(X, [-1, n_output], name="X_flat")

squared_difference = tf.square(X_flat - decoder_output,

? ? ? ? ? ? ? ? ? ? ? ? ? ? ? name="squared_difference")

reconstruction_loss = tf.reduce_sum(squared_difference,

? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?name="reconstruction_loss")

最終損失

alpha = 0.0005

loss = tf.add(margin_loss, alpha * reconstruction_loss, name="loss")

額外設(shè)置

# 全局初始化

init = tf.global_variables_initializer()

saver = tf.train.Saver()

# 計(jì)算精度

correct = tf.equal(y, y_pred, name="correct")

accuracy = tf.reduce_mean(tf.cast(correct, tf.float32), name="accuracy")

# 用 Adam 優(yōu)化器

optimizer = tf.train.AdamOptimizer()

training_op = optimizer.minimize(loss, name="training_op")

小結(jié)

以上已經(jīng)完成構(gòu)建所有的網(wǎng)絡(luò)結(jié)構(gòu)，接下來(lái)訓(xùn)練和測(cè)試的步驟都非常標(biāo)準(zhǔn)化，就不再多言了。需要提醒的是，在訓(xùn)練時(shí)，mask_with_labels 設(shè)置成 True，y 被傳出去用在重構(gòu)損失函數(shù)里，如下圖：

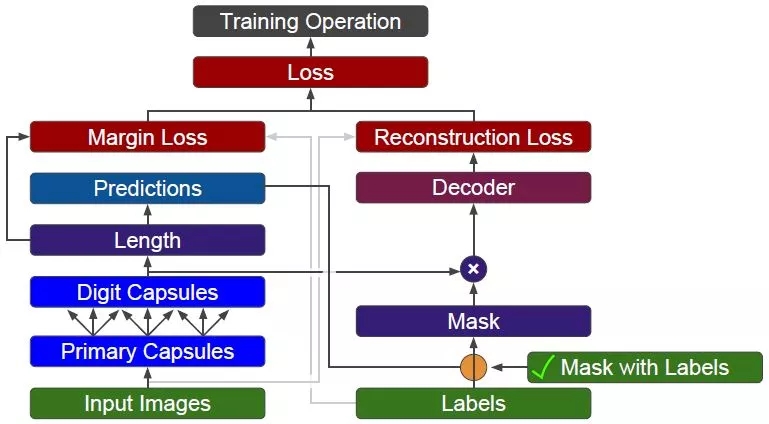
在測(cè)試時(shí)，mask_with_labels 設(shè)置成 False，y_pred 被傳出去用在重構(gòu)損失函數(shù)里，如下圖：

4、總結(jié)

深度學(xué)習(xí)，本質(zhì)就是一系列的張量變換 (tensor transformation)。Capsule 現(xiàn)在將神經(jīng)元的輸入和輸出升級(jí)成二維向量，以后很容易會(huì)將其延伸為高維張量。

在識(shí)別數(shù)字上，人只需要看幾十個(gè)最多幾百個(gè)樣例就能分辨數(shù)字。Capsule 只需要 CNN 需要的一小部分樣例就能達(dá)到同等水平，而 CNN 通常需要上萬(wàn)的數(shù)據(jù)，從這點(diǎn)看 Capsule 的運(yùn)作方式比 CNN 更接近人的大腦。此外Capsule還可以識(shí)別重疊數(shù)字。

不過(guò) CapsNet 在 ImageNet 數(shù)據(jù)集上訓(xùn)練起來(lái)太耗時(shí)，而且目前這個(gè)路由算法過(guò)于簡(jiǎn)單 (Hinton 論文坑已挖好，等著大家來(lái)填)。最有趣的是從論文結(jié)果來(lái)看，引進(jìn)重構(gòu)比沒(méi)引進(jìn)重構(gòu)的識(shí)別誤差小很多，這到底是 Capsule 的功勞，還是單單重構(gòu)的功勞？

本帖把 Capsule 的原理徹底弄清楚了，也提供了部分 tensorflow 代碼，希望對(duì)大家了解這個(gè)前言課題有所幫助。Stay Tuned!

參考文獻(xiàn)

Dynamic Routing Between Capsules. SaraSabour, Nicholas Frosst, Geoffery E.Hinton

Capsule Networks. Aurélien Géron

Implementing Capsule Networks with Tensorflow. Aurélien Géron

Uncovering the Intuition behind Capsule Networks and Inverse Graphics. Tanay Kothari

UnderstandingHinton’s Capsule Networks. Max Pechyonkin

Capsule NetworksAre Shaking up AI?—?Here’s How to Use Them. Nick Bourdakos

What is a CapsNet or Capsulte Network? Debarko De

知乎“淺析 Hinton 最近提出的 Capsule 計(jì)劃”. SIY.Z

知乎“如何看待Hinton的論文Dynamic RoutingBetween Capsules”. 云夢(mèng)局客

商業(yè)智能與數(shù)據(jù)分析群

興趣范圍包括各種讓數(shù)據(jù)產(chǎn)生價(jià)值的辦法，實(shí)際應(yīng)用案例分享與討論，分析工具，ETL工具，數(shù)據(jù)倉(cāng)庫(kù)，數(shù)據(jù)挖掘工具，報(bào)表系統(tǒng)等全方位知識(shí)

QQ群：81035754