摘要：修正線性單元，是神經(jīng)網(wǎng)絡中最常用的激活函數(shù)。顧名思義，值激活函數(shù)返回輸入的值。如同余弦函數(shù)，或簡單正弦函數(shù)激活函數(shù)為神經(jīng)網(wǎng)絡引入了周期性。此外，激活函數(shù)為零點對稱的奇函數(shù)。

在神經(jīng)網(wǎng)絡中，激活函數(shù)決定來自給定輸入集的節(jié)點的輸出，其中非線性激活函數(shù)允許網(wǎng)絡復制復雜的非線性行為。正如絕大多數(shù)神經(jīng)網(wǎng)絡借助某種形式的梯度下降進行優(yōu)化，激活函數(shù)需要是可微分（或者至少是幾乎完全可微分的）。此外，復雜的激活函數(shù)也許產(chǎn)生一些梯度消失或爆炸的問題。因此，神經(jīng)網(wǎng)絡傾向于部署若干個特定的激活函數(shù)（identity、sigmoid、ReLU 及其變體）。

下面是 26 個激活函數(shù)的圖示及其一階導數(shù)，圖的右側(cè)是一些與神經(jīng)網(wǎng)絡相關(guān)的屬性。

1. Step

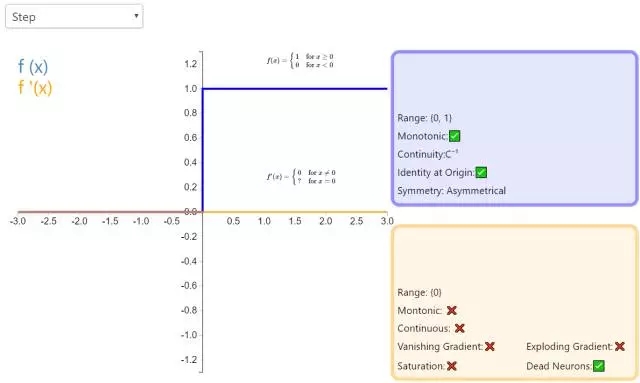
激活函數(shù) Step 更傾向于理論而不是實際，它模仿了生物神經(jīng)元要么全有要么全無的屬性。它無法應用于神經(jīng)網(wǎng)絡，因為其導數(shù)是 0（除了零點導數(shù)無定義以外），這意味著基于梯度的優(yōu)化方法并不可行。

2. Identity

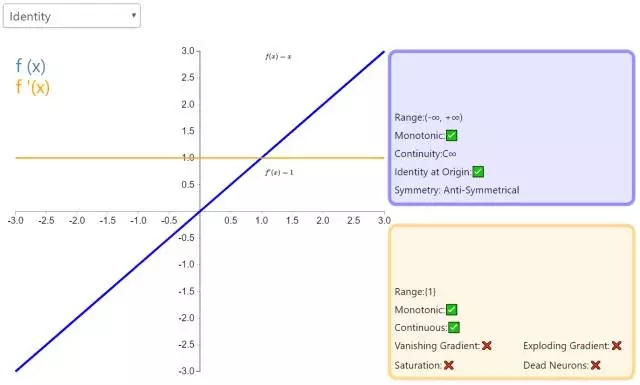
通過激活函數(shù) Identity，節(jié)點的輸入等于輸出。它完美適合于潛在行為是線性（與線性回歸相似）的任務。當存在非線性，多帶帶使用該激活函數(shù)是不夠的，但它依然可以在最終輸出節(jié)點上作為激活函數(shù)用于回歸任務。

3. ReLU

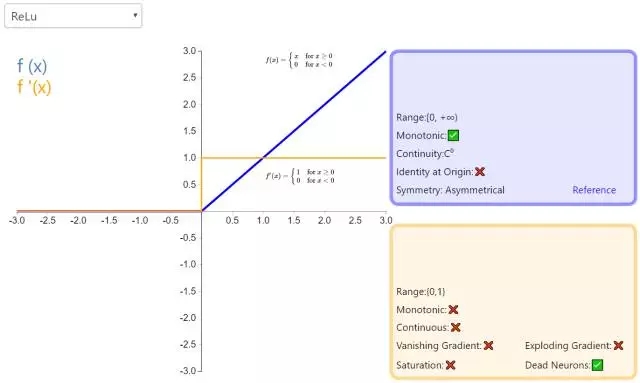
修正線性單元（Rectified linear unit，ReLU）是神經(jīng)網(wǎng)絡中最常用的激活函數(shù)。它保留了 step 函數(shù)的生物學啟發(fā)（只有輸入超出閾值時神經(jīng)元才激活），不過當輸入為正的時候，導數(shù)不為零，從而允許基于梯度的學習（盡管在 x=0 的時候，導數(shù)是未定義的）。使用這個函數(shù)能使計算變得很快，因為無論是函數(shù)還是其導數(shù)都不包含復雜的數(shù)學運算。然而，當輸入為負值的時候，ReLU 的學習速度可能會變得很慢，甚至使神經(jīng)元直接無效，因為此時輸入小于零而梯度為零，從而其權(quán)重無法得到更新，在剩下的訓練過程中會一直保持靜默。

4. Sigmoid

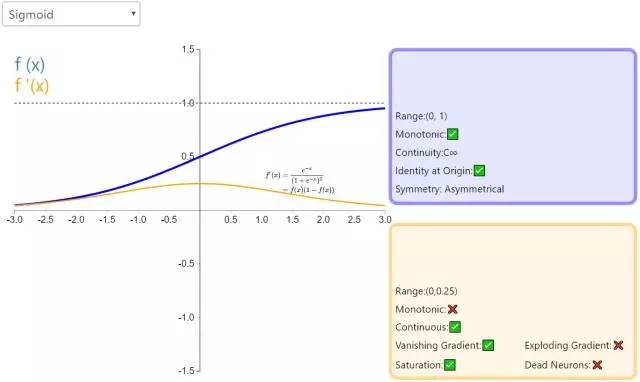
Sigmoid 因其在 logistic 回歸中的重要地位而被人熟知，值域在 0 到 1 之間。Logistic Sigmoid（或者按通常的叫法，Sigmoid）激活函數(shù)給神經(jīng)網(wǎng)絡引進了概率的概念。它的導數(shù)是非零的，并且很容易計算（是其初始輸出的函數(shù)）。然而，在分類任務中，sigmoid 正逐漸被 Tanh 函數(shù)取代作為標準的激活函數(shù)，因為后者為奇函數(shù)（關(guān)于原點對稱）。

5. Tanh

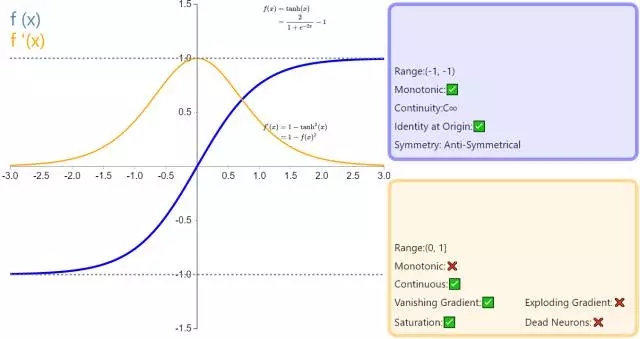
在分類任務中，雙曲正切函數(shù)（Tanh）逐漸取代 Sigmoid 函數(shù)作為標準的激活函數(shù)，其具有很多神經(jīng)網(wǎng)絡所鐘愛的特征。它是完全可微分的，反對稱，對稱中心在原點。為了解決學習緩慢和/或梯度消失問題，可以使用這個函數(shù)的更加平緩的變體（log-log、softsign、symmetrical sigmoid 等等）

6. Leaky ReLU

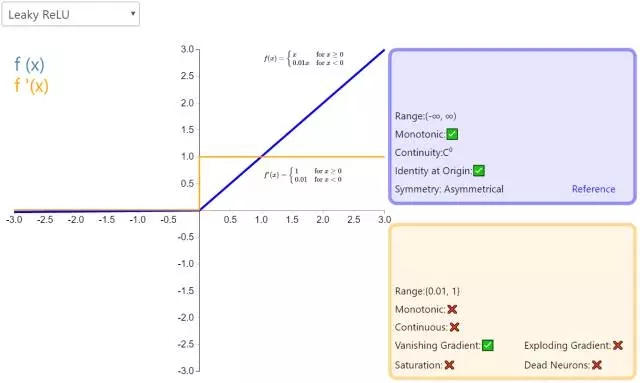
經(jīng)典（以及廣泛使用的）ReLU 激活函數(shù)的變體，帶泄露修正線性單元（Leaky ReLU）的輸出對負值輸入有很小的坡度。由于導數(shù)總是不為零，這能減少靜默神經(jīng)元的出現(xiàn)，允許基于梯度的學習（雖然會很慢）。

7. PReLU

參數(shù)化修正線性單元（Parameteric Rectified Linear Unit，PReLU）屬于 ReLU 修正類激活函數(shù)的一員。它和 RReLU 以及 Leaky ReLU 有一些共同點，即為負值輸入添加了一個線性項。而最關(guān)鍵的區(qū)別是，這個線性項的斜率實際上是在模型訓練中學習到的。

8. RReLU

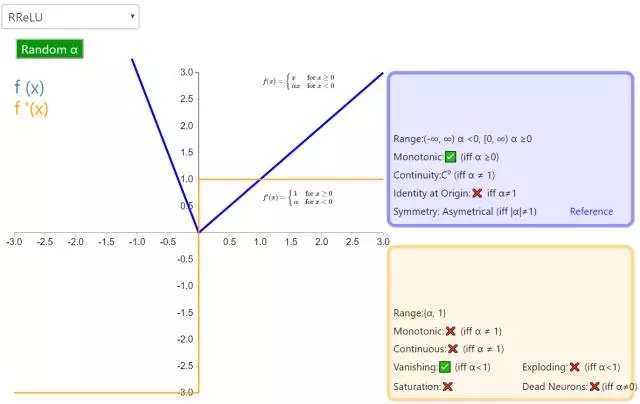
隨機帶泄露的修正線性單元（Randomized Leaky Rectified Linear Unit，RReLU）也屬于 ReLU 修正類激活函數(shù)的一員。和 Leaky ReLU 以及 PReLU 很相似，為負值輸入添加了一個線性項。而最關(guān)鍵的區(qū)別是，這個線性項的斜率在每一個節(jié)點上都是隨機分配的（通常服從均勻分布）。

9. ELU

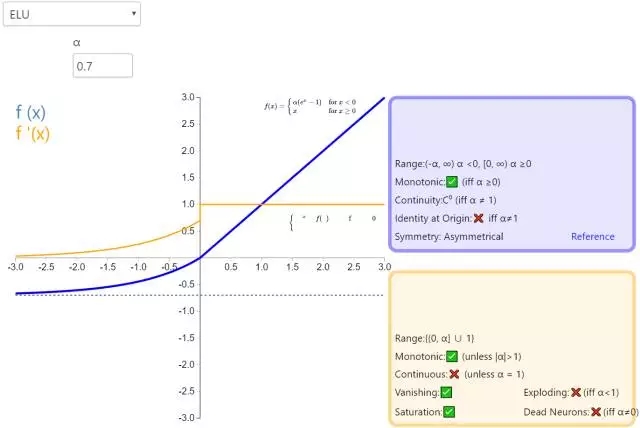
指數(shù)線性單元（Exponential Linear Unit，ELU）也屬于 ReLU 修正類激活函數(shù)的一員。和 PReLU 以及 RReLU 類似，為負值輸入添加了一個非零輸出。和其它修正類激活函數(shù)不同的是，它包括一個負指數(shù)項，從而防止靜默神經(jīng)元出現(xiàn)，導數(shù)收斂為零，從而提高學習效率。

10. SELU

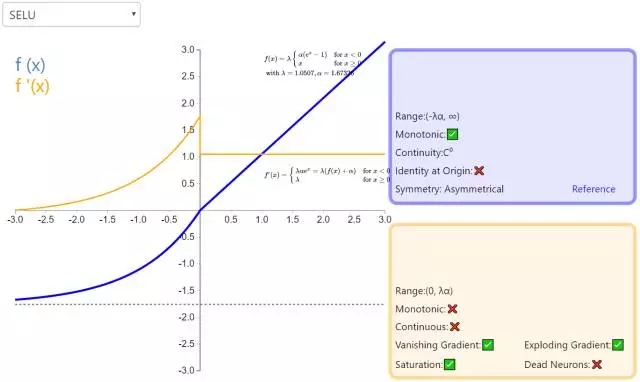
擴展指數(shù)線性單元（Scaled Exponential Linear Unit，SELU）是激活函數(shù)指數(shù)線性單元（ELU）的一個變種。其中λ和α是固定數(shù)值（分別為 1.0507 和 1.6726）。這些值背后的推論（零均值/單位方差）構(gòu)成了自歸一化神經(jīng)網(wǎng)絡的基礎（SNN）。

11. SReLU

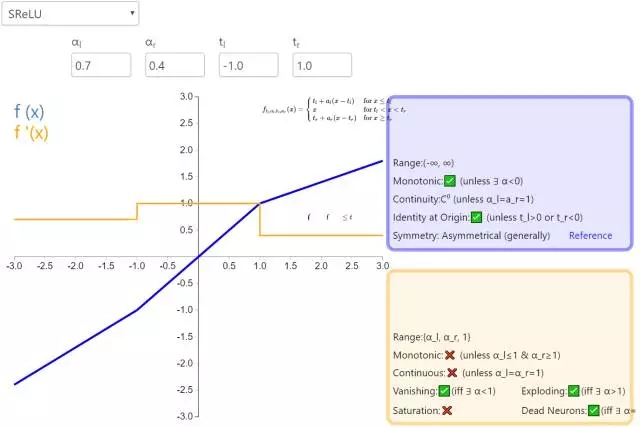
S 型整流線性激活單元（S-shaped Rectified Linear Activation Unit，SReLU）屬于以 ReLU 為代表的整流激活函數(shù)族。它由三個分段線性函數(shù)組成。其中兩種函數(shù)的斜度，以及函數(shù)相交的位置會在模型訓練中被學習。

12. Hard Sigmoid

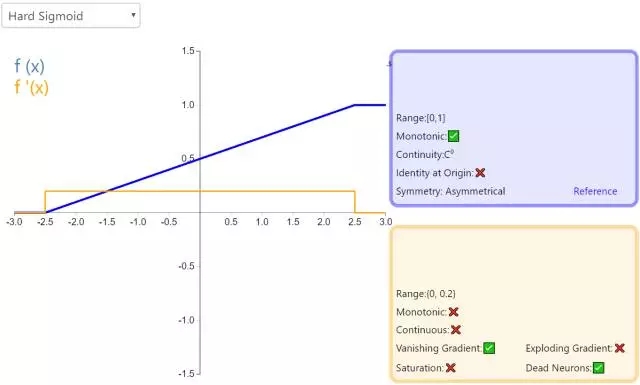
Hard Sigmoid 是 Logistic Sigmoid 激活函數(shù)的分段線性近似。它更易計算，這使得學習計算的速度更快，盡管首次派生值為零可能導致靜默神經(jīng)元/過慢的學習速率（詳見 ReLU）。

13. Hard Tanh

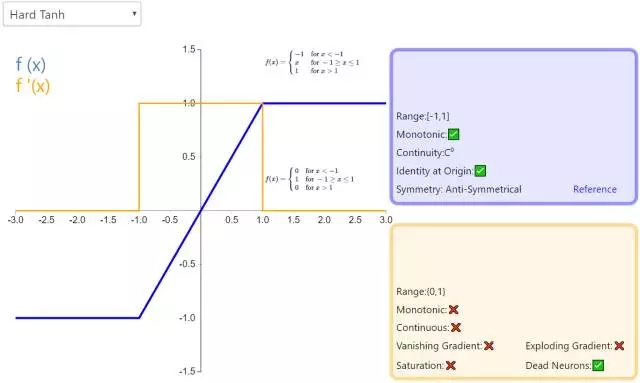
Hard Tanh 是 Tanh 激活函數(shù)的線性分段近似。相較而言，它更易計算，這使得學習計算的速度更快，盡管首次派生值為零可能導致靜默神經(jīng)元/過慢的學習速率（詳見 ReLU）。

14. LeCun Tanh

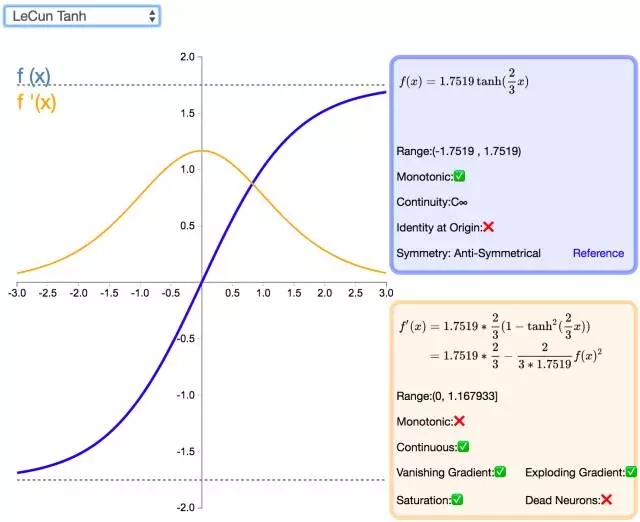
LeCun Tanh（也被稱作 Scaled Tanh）是 Tanh 激活函數(shù)的擴展版本。它具有以下幾個可以改善學習的屬性：f(± 1) = ±1；二階導數(shù)在 x=1 較大化；且有效增益接近 1。

15. ArcTan

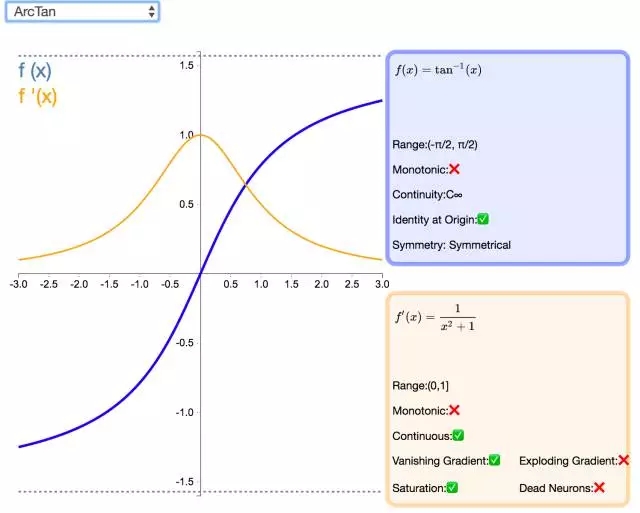
視覺上類似于雙曲正切（Tanh）函數(shù)，ArcTan 激活函數(shù)更加平坦，這讓它比其他雙曲線更加清晰。在默認情況下，其輸出范圍在-π/2 和π/2 之間。其導數(shù)趨向于零的速度也更慢，這意味著學習的效率更高。但這也意味著，導數(shù)的計算比 Tanh 更加昂貴。

16. Softsign

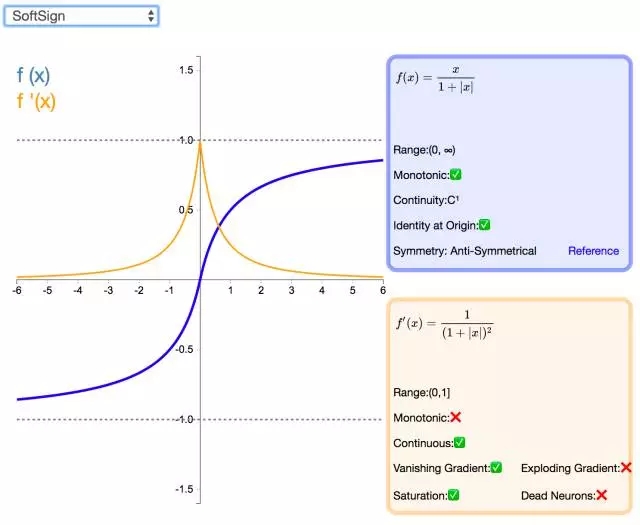
Softsign 是 Tanh 激活函數(shù)的另一個替代選擇。就像 Tanh 一樣，Softsign 是反對稱、去中心、可微分，并返回-1 和 1 之間的值。其更平坦的曲線與更慢的下降導數(shù)表明它可以更高效地學習。另一方面，導數(shù)的計算比 Tanh 更麻煩。

17. SoftPlus

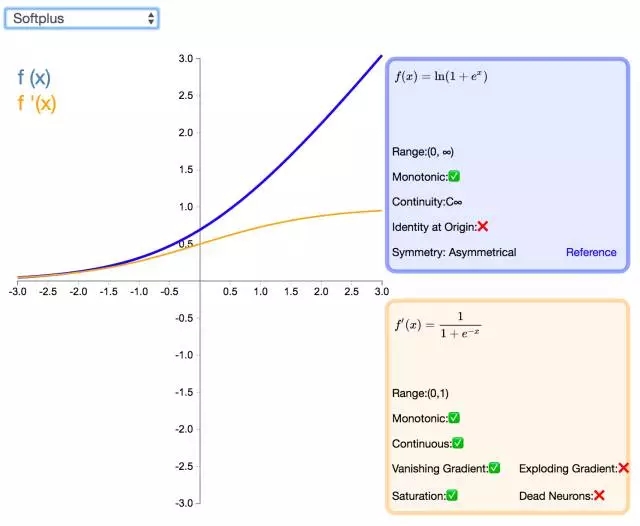
作為 ReLU 的一個不錯的替代選擇，SoftPlus 能夠返回任何大于 0 的值。與 ReLU 不同，SoftPlus 的導數(shù)是連續(xù)的、非零的，無處不在，從而防止出現(xiàn)靜默神經(jīng)元。然而，SoftPlus 另一個不同于 ReLU 的地方在于其不對稱性，不以零為中心，這興許會妨礙學習。此外，由于導數(shù)常常小于 1，也可能出現(xiàn)梯度消失的問題。

18. Signum

激活函數(shù) Signum（或者簡寫為 Sign）是二值階躍激活函數(shù)的擴展版本。它的值域為 [-1,1]，原點值是 0。盡管缺少階躍函數(shù)的生物動機，Signum 依然是反對稱的，這對激活函數(shù)來說是一個有利的特征。

19. Bent Identity

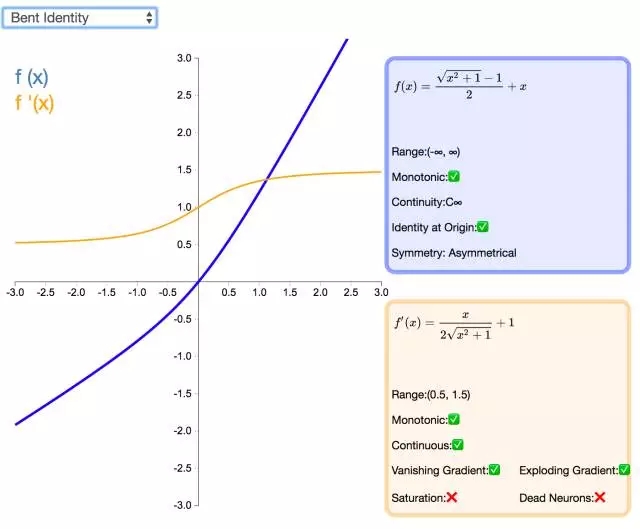
激活函數(shù) Bent Identity 是介于 Identity 與 ReLU 之間的一種折衷選擇。它允許非線性行為，盡管其非零導數(shù)有效提升了學習并克服了與 ReLU 相關(guān)的靜默神經(jīng)元的問題。由于其導數(shù)可在 1 的任意一側(cè)返回值，因此它可能容易受到梯度爆炸和消失的影響。

20. Symmetrical Sigmoid

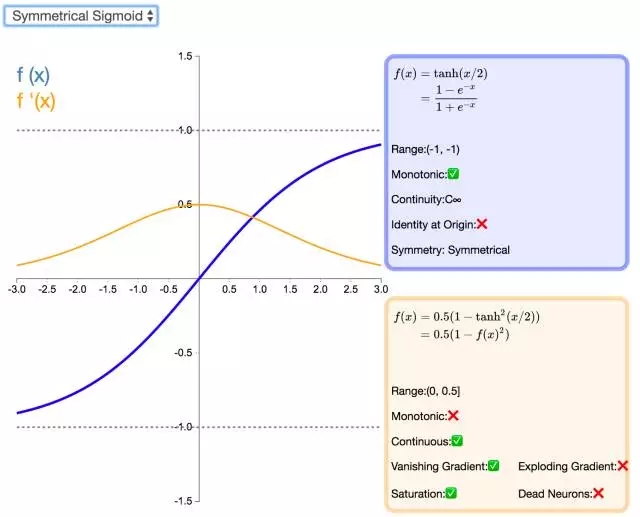
Symmetrical Sigmoid 是另一個 Tanh 激活函數(shù)的變種（實際上，它相當于輸入減半的 Tanh）。和 Tanh 一樣，它是反對稱的、零中心、可微分的，值域在 -1 到 1 之間。它更平坦的形狀和更慢的下降派生表明它可以更有效地進行學習。

21. Log Log

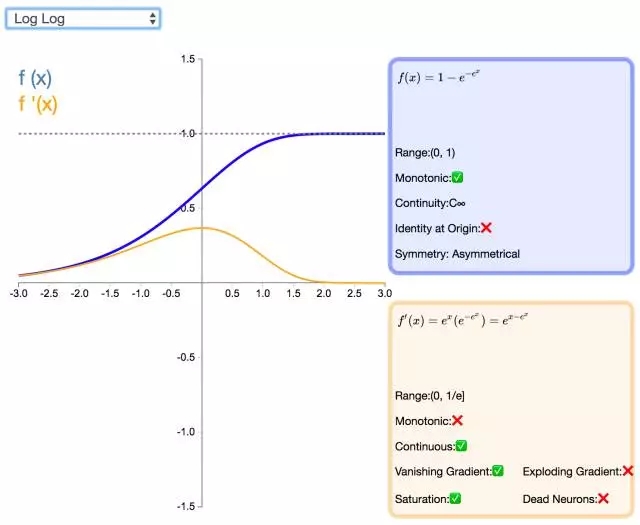
Log Log 激活函數(shù)（由上圖 f(x) 可知該函數(shù)為以 e 為底的嵌套指數(shù)函數(shù)）的值域為 [0,1]，Complementary Log Log 激活函數(shù)有潛力替代經(jīng)典的 Sigmoid 激活函數(shù)。該函數(shù)飽和地更快，且零點值要高于 0.5。

22. Gaussian

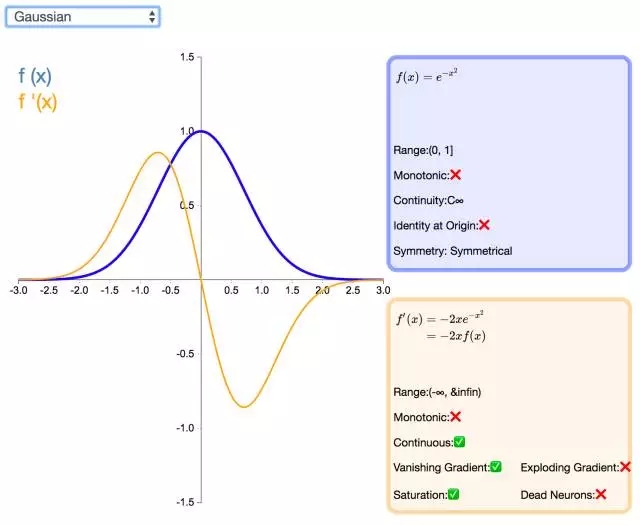
高斯激活函數(shù)（Gaussian）并不是徑向基函數(shù)網(wǎng)絡（RBFN）中常用的高斯核函數(shù)，高斯激活函數(shù)在多層感知機類的模型中并不是很流行。該函數(shù)處處可微且為偶函數(shù)，但一階導會很快收斂到零。

23. Absolute

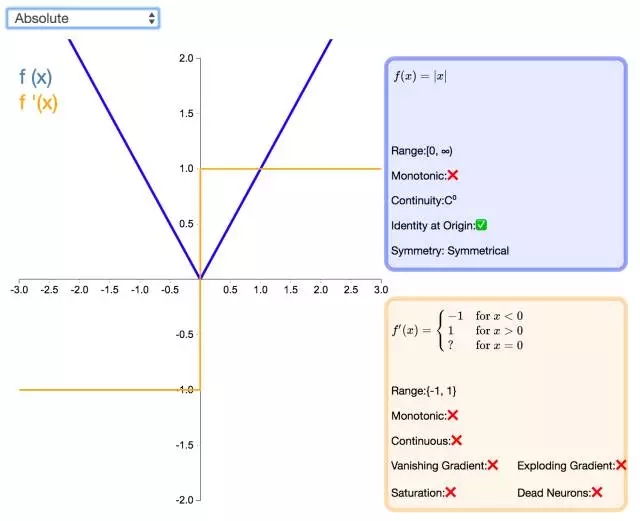
顧名思義，值（Absolute）激活函數(shù)返回輸入的值。該函數(shù)的導數(shù)除了零點外處處有定義，且導數(shù)的量值處處為 1。這種激活函數(shù)一定不會出現(xiàn)梯度爆炸或消失的情況。

24. Sinusoid

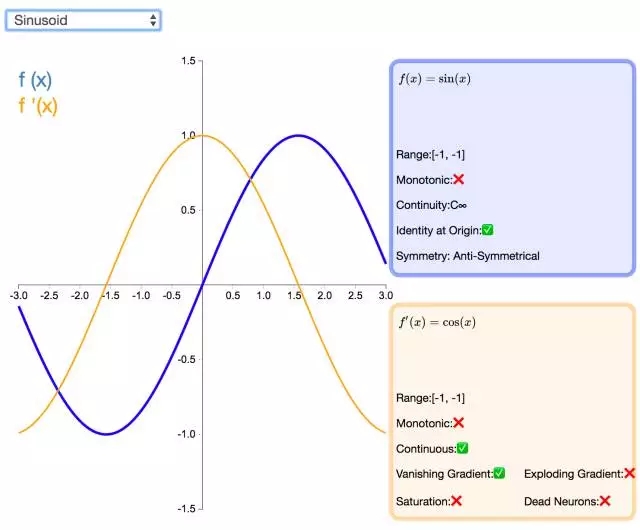
如同余弦函數(shù)，Sinusoid（或簡單正弦函數(shù)）激活函數(shù)為神經(jīng)網(wǎng)絡引入了周期性。該函數(shù)的值域為 [-1,1]，且導數(shù)處處連續(xù)。此外，Sinusoid 激活函數(shù)為零點對稱的奇函數(shù)。

25. Cos

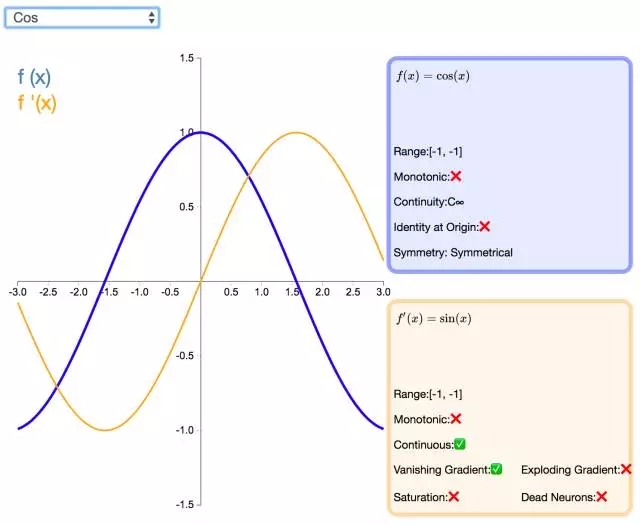
如同正弦函數(shù)，余弦激活函數(shù)（Cos/Cosine）為神經(jīng)網(wǎng)絡引入了周期性。它的值域為 [-1,1]，且導數(shù)處處連續(xù)。和 Sinusoid 函數(shù)不同，余弦函數(shù)為不以零點對稱的偶函數(shù)。

26. Sinc

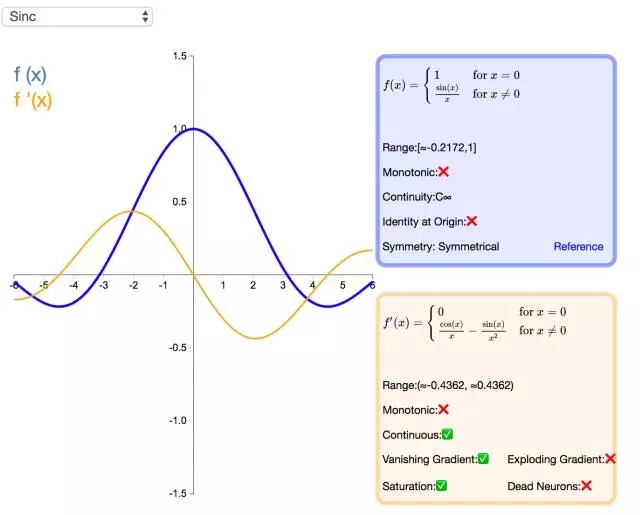
Sinc 函數(shù)（全稱是 Cardinal Sine）在信號處理中尤為重要，因為它表征了矩形函數(shù)的傅立葉變換（Fourier transform）。作為一種激活函數(shù)，它的優(yōu)勢在于處處可微和對稱的特性，不過它比較容易產(chǎn)生梯度消失的問題。

原文鏈接：https://dashee87.github.io/data%20science/deep%20learning/visualising-activation-functions-in-neural-networks/

商業(yè)智能與數(shù)據(jù)分析群

興趣范圍包括各種讓數(shù)據(jù)產(chǎn)生價值的辦法，實際應用案例分享與討論，分析工具，ETL工具，數(shù)據(jù)倉庫，數(shù)據(jù)挖掘工具，報表系統(tǒng)等全方位知識

QQ群：81035754