摘要：測度是高維空間中長度面積體積概念的拓廣，可以理解為超體積。前作其實已經針對第二點提出了一個解決方案，就是對生成樣本和真實樣本加噪聲，直觀上說，使得原本的兩個低維流形彌散到整個高維空間，強行讓它們產生不可忽略的重疊。

在GAN的相關研究如火如荼甚至可以說是泛濫的今天，一篇新鮮出爐的arXiv論文《Wasserstein GAN》卻在Reddit的Machine Learning頻道火了，連Goodfellow都在帖子里和大家熱烈討論，這篇論文究竟有什么了不得的地方呢？?

要知道自從2014年Ian Goodfellow提出以來，GAN就存在著訓練困難、生成器和判別器的loss無法指示訓練進程、生成樣本缺乏多樣性等問題。從那時起，很多論文都在嘗試解決，但是效果不盡人意，比如最有名的一個改進DCGAN依靠的是對判別器和生成器的架構進行實驗枚舉，最終找到一組比較好的網絡架構設置，但是實際上是治標不治本，沒有徹底解決問題。而今天的主角Wasserstein GAN（下面簡稱WGAN）成功地做到了以下爆炸性的幾點：

徹底解決GAN訓練不穩定的問題，不再需要小心平衡生成器和判別器的訓練程度

基本解決了collapse mode的問題，確保了生成樣本的多樣性?

訓練過程中終于有一個像交叉熵、準確率這樣的數值來指示訓練的進程，這個數值越小代表GAN訓練得越好，代表生成器產生的圖像質量越高（如題圖所示）

以上一切好處不需要精心設計的網絡架構，最簡單的多層全連接網絡就可以做到

那以上好處來自哪里？這就是令人拍案叫絕的部分了——實際上作者整整花了兩篇論文，在第一篇《Towards Principled Methods for Training Generative Adversarial Networks》里面推了一堆公式定理，從理論上分析了原始GAN的問題所在，從而針對性地給出了改進要點；在這第二篇《Wasserstein GAN》里面，又再從這個改進點出發推了一堆公式定理，最終給出了改進的算法實現流程，而改進后相比原始GAN的算法實現流程卻只改了四點：

判別器最后一層去掉sigmoid

生成器和判別器的loss不取log

每次更新判別器的參數之后把它們的值截斷到不超過一個固定常數c

不要用基于動量的優化算法（包括momentum和Adam），推薦RMSProp，SGD也行

算法截圖如下：

改動是如此簡單，效果卻驚人地好，以至于Reddit上不少人在感嘆：就這樣？沒有別的了？ 太簡單了吧！這些反應讓我想起了一個頗有年頭的雞湯段子，說是一個工程師在電機外殼上用粉筆劃了一條線排除了故障，要價一萬美元——畫一條線，1美元；知道在哪畫線，9999美元。上面這四點改進就是作者Martin Arjovsky劃的簡簡單單四條線，對于工程實現便已足夠，但是知道在哪劃線，背后卻是精巧的數學分析，而這也是本文想要整理的內容。

本文內容分為五個部分：

原始GAN究竟出了什么問題？（此部分較長）

WGAN之前的一個過渡解決方案?

Wasserstein距離的優越性質

從Wasserstein距離到WGAN

總結

理解原文的很多公式定理需要對測度論、 拓撲學等數學知識有所掌握，本文會從直觀的角度對每一個重要公式進行解讀，有時通過一些低維的例子幫助讀者理解數學背后的思想，所以不免會失于嚴謹，如有引喻不當之處，歡迎在評論中指出。

以下簡稱《Wassertein GAN》為“WGAN本作”，簡稱《Towards Principled Methods for Training Generative Adversarial Networks》為“WGAN前作”。

WGAN源碼實現：martinarjovsky/WassersteinGAN

第一部分：原始GAN究竟出了什么問題？

第一種原始GAN形式的問題

一句話概括：判別器越好，生成器梯度消失越嚴重。WGAN前作從兩個角度進行了論證，第一個角度是從生成器的等價損失函數切入的。

首先從公式1可以得到，在生成器G固定參數時最優的判別器D應該是什么。對于一個具體的樣本，它可能來自真實分布也可能來自生成分布，它對公式1損失函數的貢獻是

然而GAN訓練有一個trick，就是別把判別器訓練得太好，否則在實驗中生成器會完全學不動（loss降不下去），為了探究背后的原因，我們就可以看看在極端情況——判別器最優時，生成器的損失函數變成什么。給公式2加上一個不依賴于生成器的項，使之變成

流形（manifold）是高維空間中曲線、曲面概念的拓廣，我們可以在低維上直觀理解這個概念，比如我們說三維空間中的一個曲面是一個二維流形，因為它的本質維度（intrinsic dimension）只有2，一個點在這個二維流形上移動只有兩個方向的自由度。同理，三維空間或者二維空間中的一條曲線都是一個一維流形。

測度（measure）是高維空間中長度、面積、體積概念的拓廣，可以理解為“超體積”。

接著作者寫了很多公式定理從第二個角度進行論證，但是背后的思想也可以直觀地解釋：

有了這些理論分析，原始GAN不穩定的原因就徹底清楚了：判別器訓練得太好，生成器梯度消失，生成器loss降不下去；判別器訓練得不好，生成器梯度不準，四處亂跑。只有判別器訓練得不好不壞才行，但是這個火候又很難把握，甚至在同一輪訓練的前后不同階段這個火候都可能不一樣，所以GAN才那么難訓練。

實驗輔證如下：

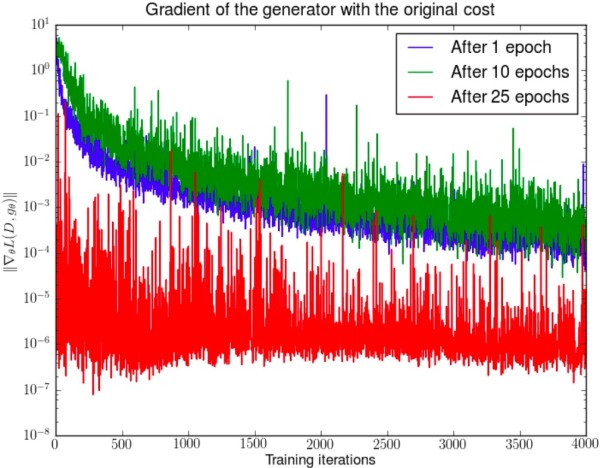
WGAN前作Figure 2。先分別將DCGAN訓練1，20，25個epoch，然后固定生成器不動，判別器重新隨機初始化從頭開始訓練，對于第一種形式的生成器loss產生的梯度可以打印出其尺度的變化曲線，可以看到隨著判別器的訓練，生成器的梯度均迅速衰減。注意y軸是對數坐標軸。

第二種原始GAN形式的問題

一句話概括：最小化第二種生成器loss函數，會等價于最小化一個不合理的距離衡量，導致兩個問題，一是梯度不穩定，二是collapse mode即多樣性不足。WGAN前作又是從兩個角度進行了論證，下面只說第一個角度，因為對于第二個角度我難以找到一個直觀的解釋方式，感興趣的讀者還是去看論文吧（逃）。

第一部分小結：在原始GAN的（近似）最優判別器下，第一種生成器loss面臨梯度消失問題，第二種生成器loss面臨優化目標荒謬、梯度不穩定、對多樣性與準確性懲罰不平衡導致mode collapse這幾個問題。

實驗輔證如下：

WGAN前作Figure 3。先分別將DCGAN訓練1，20，25個epoch，然后固定生成器不動，判別器重新隨機初始化從頭開始訓練，對于第二種形式的生成器loss產生的梯度可以打印出其尺度的變化曲線，可以看到隨著判別器的訓練，藍色和綠色曲線中生成器的梯度迅速增長，說明梯度不穩定，紅線對應的是DCGAN相對收斂的狀態，梯度才比較穩定。

第二部分：WGAN之前的一個過渡解決方案?

原始GAN問題的根源可以歸結為兩點，一是等價優化的距離衡量（KL散度、JS散度）不合理，二是生成器隨機初始化后的生成分布很難與真實分布有不可忽略的重疊。

WGAN前作其實已經針對第二點提出了一個解決方案，就是對生成樣本和真實樣本加噪聲，直觀上說，使得原本的兩個低維流形“彌散”到整個高維空間，強行讓它們產生不可忽略的重疊。而一旦存在重疊，JS散度就能真正發揮作用，此時如果兩個分布越靠近，它們“彌散”出來的部分重疊得越多，JS散度也會越小而不會一直是一個常數，于是（在第一種原始GAN形式下）梯度消失的問題就解決了。在訓練過程中，我們可以對所加的噪聲進行退火（annealing），慢慢減小其方差，到后面兩個低維流形“本體”都已經有重疊時，就算把噪聲完全拿掉，JS散度也能照樣發揮作用，繼續產生有意義的梯度把兩個低維流形拉近，直到它們接近完全重合。以上是對原文的直觀解釋。

在這個解決方案下我們可以放心地把判別器訓練到接近最優，不必擔心梯度消失的問題。而當判別器最優時，對公式9取反可得判別器的最小loss為

第三部分：Wasserstein距離的優越性質

第四部分：從Wasserstein距離到WGAN

既然Wasserstein距離有如此優越的性質，如果我們能夠把它定義為生成器的loss，不就可以產生有意義的梯度來更新生成器，使得生成分布被拉向真實分布嗎？

上文說過，WGAN與原始GAN第一種形式相比，只改了四點：

判別器最后一層去掉sigmoid

生成器和判別器的loss不取log

每次更新判別器的參數之后把它們的值截斷到不超過一個固定常數c

不要用基于動量的優化算法（包括momentum和Adam），推薦RMSProp，SGD也行

前三點都是從理論分析中得到的，已經介紹完畢；第四點卻是作者從實驗中發現的，屬于trick，相對比較“玄”。作者發現如果使用Adam，判別器的loss有時候會崩掉，當它崩掉時，Adam給出的更新方向與梯度方向夾角的cos值就變成負數，更新方向與梯度方向南轅北轍，這意味著判別器的loss梯度是不穩定的，所以不適合用Adam這類基于動量的優化算法。作者改用RMSProp之后，問題就解決了，因為RMSProp適合梯度不穩定的情況。

對WGAN作者做了不少實驗驗證，本文只提比較重要的三點。第一，判別器所近似的Wasserstein距離與生成器的生成圖片質量高度相關，如下所示（此即題圖）：

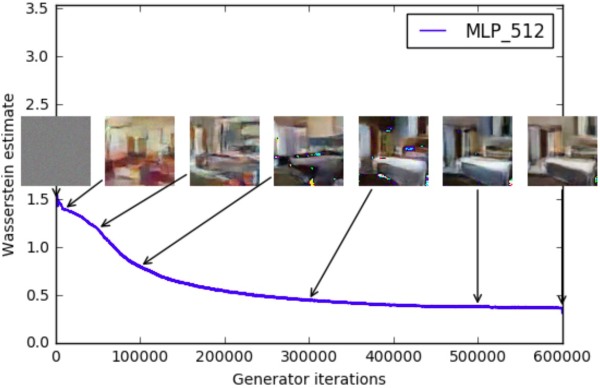
最后補充一點論文沒提到，但是我個人覺得比較微妙的問題。判別器所近似的Wasserstein距離能夠用來指示單次訓練中的訓練進程，這個沒錯；接著作者又說它可以用于比較多次訓練進程，指引調參，我倒是覺得需要小心些。比如說我下次訓練時改了判別器的層數、節點數等超參，判別器的擬合能力就必然有所波動，再比如說我下次訓練時改了生成器兩次迭代之間，判別器的迭代次數，這兩種常見的變動都會使得Wasserstein距離的擬合誤差就與上次不一樣。那么這個擬合誤差的變動究竟有多大，或者說不同的人做實驗時判別器的擬合能力或迭代次數相差實在太大，那它們之間還能不能直接比較上述指標，我都是存疑的。

第五部分：總結

WGAN前作分析了Ian Goodfellow提出的原始GAN兩種形式各自的問題，第一種形式等價在最優判別器下等價于最小化生成分布與真實分布之間的JS散度，由于隨機生成分布很難與真實分布有不可忽略的重疊以及JS散度的突變特性，使得生成器面臨梯度消失的問題；第二種形式在最優判別器下等價于既要最小化生成分布與真實分布直接的KL散度，又要較大化其JS散度，相互矛盾，導致梯度不穩定，而且KL散度的不對稱性使得生成器寧可喪失多樣性也不愿喪失準確性，導致collapse mode現象。

WGAN前作針對分布重疊問題提出了一個過渡解決方案，通過對生成樣本和真實樣本加噪聲使得兩個分布產生重疊，理論上可以解決訓練不穩定的問題，可以放心訓練判別器到接近最優，但是未能提供一個指示訓練進程的可靠指標，也未做實驗驗證。

WGAN本作引入了Wasserstein距離，由于它相對KL散度與JS散度具有優越的平滑特性，理論上可以解決梯度消失問題。接著通過數學變換將Wasserstein距離寫成可求解的形式，利用一個參數數值范圍受限的判別器神經網絡來較大化這個形式，就可以近似Wasserstein距離。在此近似最優判別器下優化生成器使得Wasserstein距離縮小，就能有效拉近生成分布與真實分布。WGAN既解決了訓練不穩定的問題，也提供了一個可靠的訓練進程指標，而且該指標確實與生成樣本的質量高度相關。作者對WGAN進行了實驗驗證。

商業智能與數據分析群

興趣范圍包括各種讓數據產生價值的辦法，實際應用案例分享與討論，分析工具，ETL工具，數據倉庫，數據挖掘工具，報表系統等全方位知識

QQ群：81035754