摘要：在最近的一次人工智能會(huì)議上，表示自己對(duì)于反向傳播非常懷疑，并提出應(yīng)該拋棄它并重新開(kāi)始。在人工智能多年的發(fā)展過(guò)程中，反向傳播已經(jīng)成為了深度學(xué)習(xí)不可或缺的一部分。最后，我們會(huì)將這些規(guī)則組合成可用于任意神經(jīng)網(wǎng)絡(luò)的反向傳播算法。

現(xiàn)在的深度學(xué)習(xí)發(fā)展似乎已經(jīng)陷入了大型化、深度化的怪圈，我們?cè)O(shè)計(jì)的模型容易被對(duì)抗樣本欺騙，同時(shí)又需要大量的訓(xùn)練數(shù)據(jù)——在無(wú)監(jiān)督學(xué)習(xí)上我們?nèi)〉玫耐黄七€很少。作為反向傳播這一深度學(xué)習(xí)核心技術(shù)的提出者之一，Geoffrey Hinton 很早就意識(shí)到反向傳播并不是自然界生物大腦中存在的機(jī)制。那么，在技術(shù)上，反向傳播還有哪些值得懷疑的地方？

反向傳播的可疑之處

Geoffrey Hinton 對(duì)人工智能的未來(lái)非常擔(dān)憂。在最近的一次人工智能會(huì)議上，Hinton 表示自己對(duì)于反向傳播「非常懷疑」，并提出「應(yīng)該拋棄它并重新開(kāi)始」。

在人工智能多年的發(fā)展過(guò)程中，反向傳播已經(jīng)成為了深度學(xué)習(xí)不可或缺的一部分。研究人員發(fā)現(xiàn)，只要層是可微分的，我們就可以在求解時(shí)使用任何計(jì)算層。換句話說(shuō)，層的梯度是可以被計(jì)算的。更為清楚地說(shuō)，在尋物游戲中，準(zhǔn)確表現(xiàn)出被蒙住眼睛的玩家與他的目標(biāo)之間的距離。

在反向傳播上，存在著幾個(gè)問(wèn)題：第一個(gè)是計(jì)算出來(lái)的梯度是否真的是學(xué)習(xí)的正確方向。這在直觀上是可疑的。人們總是可以尋找到某些看起來(lái)可行的方向，但這并不總是意味著它最終通向問(wèn)題的解。所以，忽略梯度或許也可以讓我們找到解決方案（當(dāng)然，我們也不能永遠(yuǎn)忽略梯度）。適應(yīng)性方法和優(yōu)化方法之間存在著很多不同。

現(xiàn)在，讓我們回顧一下反向傳播思想的起源。歷史上，機(jī)器學(xué)習(xí)起源于曲線擬合的整體思路。在線性回歸的具體情況下（如對(duì)一條線進(jìn)行擬合預(yù)測(cè)），計(jì)算梯度是求解最小二乘問(wèn)題。在優(yōu)化領(lǐng)域，除了使用梯度找到最優(yōu)解之外，還有許多其他方法。不過(guò)，事實(shí)上，隨機(jī)梯度下降可能是最基本的優(yōu)化方法之一。所以它只是我們能想到的很多方法中更為簡(jiǎn)單的一個(gè)，雖然也非常好用。

大多數(shù)研究?jī)?yōu)化的學(xué)者很長(zhǎng)一段時(shí)間以來(lái)都認(rèn)為深度學(xué)習(xí)的高維空間需要非凸解，因此非常難以優(yōu)化。但是，由于一些難以解釋的原因。深度學(xué)習(xí)使用隨機(jī)梯度下降（SGD）的效果卻非常好。許多研究人員對(duì)于為什么深度學(xué)習(xí)用 SGD 優(yōu)化如此簡(jiǎn)單提出了不同解釋，其中最具說(shuō)服力的說(shuō)法是這種方法傾向于找到真正的鞍點(diǎn)——而不是小范圍內(nèi)的谷地。使用這種方法的情況下，總是有足夠的維度讓我們找到最優(yōu)解。

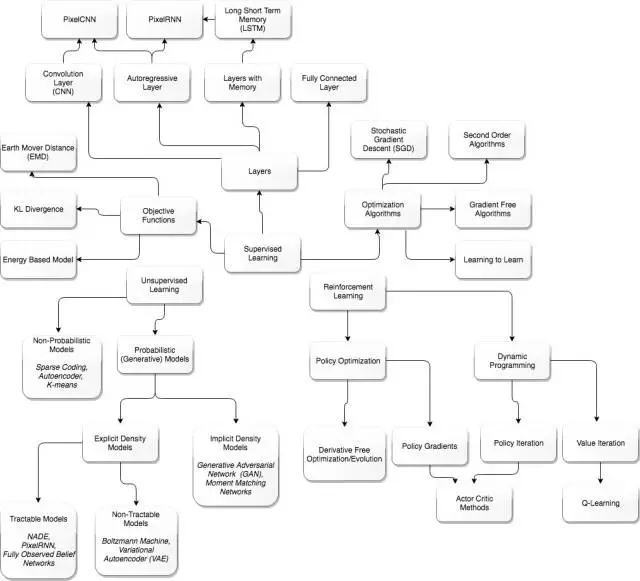
一張指導(dǎo)圖，防止迷失

DeepMind 研究的合成梯度是一種解耦層方法，以便于我們不總是需要反向傳播，或者梯度計(jì)算可推遲。這種方法同樣非常有效。這一發(fā)現(xiàn)可能也是一種暗示，正在產(chǎn)生更通用的方法。好像關(guān)于這個(gè)方向的任何升級(jí)都是有益的（隨意提了一下合成梯度），不管效果是不是一樣。

還有一個(gè)使用目標(biāo)函數(shù)的典型問(wèn)題：反向傳播是相對(duì)于目標(biāo)函數(shù)計(jì)算的。通常，目標(biāo)函數(shù)是預(yù)測(cè)分布與實(shí)際分布之間差異的量度。通常，它是從 Kullback-Liebler 散度衍生出來(lái)的，或者是像 Wassertsein 這樣的其他相似性分布數(shù)值。但是，在這些相似性計(jì)算中，「標(biāo)簽」是監(jiān)督訓(xùn)練必不可少的一部分。在 Hinton 拋出反向傳播言論的同時(shí)，他也對(duì)于監(jiān)督學(xué)習(xí)發(fā)表了自己的看法：「我認(rèn)為這意味著放棄反向傳播……我們確實(shí)不需要所有數(shù)據(jù)都有標(biāo)簽。」

簡(jiǎn)而言之，沒(méi)有目標(biāo)函數(shù)就無(wú)法進(jìn)行反向傳播。如果你無(wú)法評(píng)估預(yù)測(cè)值和標(biāo)簽（實(shí)際或訓(xùn)練數(shù)據(jù)）的 value 值，你就沒(méi)有目標(biāo)函數(shù)。因此，為了實(shí)現(xiàn)「無(wú)監(jiān)督學(xué)習(xí)」，你需要拋棄計(jì)算梯度的能力。

但是，在我們把這一重要能力丟掉之前，先從更通用的角度看一下目標(biāo)函數(shù)的目的。目標(biāo)函數(shù)是對(duì)自動(dòng)化內(nèi)部模型預(yù)測(cè)所處環(huán)境的準(zhǔn)確率的評(píng)估。任何智能自動(dòng)化的目的都是構(gòu)建準(zhǔn)確率高的內(nèi)部模型。但是，模型和它一直或持續(xù)所處的環(huán)境之間不需要任何評(píng)估。也就是說(shuō)，自動(dòng)化不需要執(zhí)行反向傳播進(jìn)行學(xué)習(xí)。自動(dòng)化可以通過(guò)其他途徑改善其內(nèi)部模型。

其他途徑就是「想象力」（imagination）或「做夢(mèng)」（dreaming），不用立刻把預(yù)測(cè)與事實(shí)對(duì)比然后更新參數(shù)。今天最接近的體現(xiàn)就是生成對(duì)抗網(wǎng)絡(luò)（GAN）。GAN 包括兩個(gè)網(wǎng)絡(luò)：生成器和鑒別器。你可以把鑒別器當(dāng)作使用目標(biāo)函數(shù)的神經(jīng)網(wǎng)絡(luò)，即它可以用現(xiàn)實(shí)驗(yàn)證內(nèi)部生成器網(wǎng)絡(luò)。生成器自動(dòng)化創(chuàng)造近似現(xiàn)實(shí)。GAN 網(wǎng)絡(luò)使用反向傳播，執(zhí)行無(wú)監(jiān)督學(xué)習(xí)。因此，無(wú)監(jiān)督學(xué)習(xí)可能不需要目標(biāo)函數(shù)，但它或許仍然需要反向傳播。

看待無(wú)監(jiān)督學(xué)習(xí)的另一種方式是，某種程度上，它是一種元學(xué)習(xí)。系統(tǒng)不需要監(jiān)督訓(xùn)練數(shù)據(jù)的一種可能原因是學(xué)習(xí)算法已經(jīng)開(kāi)發(fā)出自己的較佳內(nèi)部模型。也就是說(shuō)，仍然存在一定程度的監(jiān)督，只不過(guò)在學(xué)習(xí)算法中更加隱晦。學(xué)習(xí)算法如何具備這種能力尚不可知。

總之，現(xiàn)在判斷我們是否可以拋棄反向傳播還為時(shí)尚早。我們當(dāng)然可以使用沒(méi)有那么嚴(yán)格的反向傳播（即合成梯度或其他啟發(fā)）。但是，逐步學(xué)習(xí)（或稱爬山法）仍然是必要的。我當(dāng)然對(duì)找到駁斥逐步學(xué)習(xí)或爬山法的研究很感興趣。這實(shí)際上可以類比為宇宙的運(yùn)行，具體來(lái)說(shuō)就是熱力學(xué)的第二定律。再具體點(diǎn)就是熵一直在提高。信息引擎將降低熵，以交換所處環(huán)境中的熵提高。因此，沒(méi)有一種方法可以完全避免梯度，除非存在「永動(dòng)信息機(jī)器」（perpetual motion information machine）。

Hinton 與他的谷歌同事 Sara Sabour 和 Nicholas Frosst 共同完成的論文《Dynamic Routing Between Capsules》已被 NIPS 2017 大會(huì)接收，他們?cè)谘芯恐刑岢龅?capsule 概念正是 Hinton 對(duì)于未來(lái)人工智能形態(tài)的探索。不可否認(rèn)的是，在無(wú)監(jiān)督學(xué)習(xí)的道路上，我們還有很長(zhǎng)的一段路要走。

反向傳播的推導(dǎo)過(guò)程

神經(jīng)網(wǎng)絡(luò)在權(quán)重的變化和目標(biāo)函數(shù)的變化之間不再是線性關(guān)系。在特定層級(jí)的任何擾動(dòng)（perturbation）將會(huì)在連續(xù)層級(jí)中進(jìn)一步變化。那么，我們?cè)撊绾斡?jì)算神經(jīng)網(wǎng)絡(luò)中所有權(quán)重的梯度，從而進(jìn)一步使用梯度下降法（最速下降法）呢？這也就是我們?yōu)槭裁匆褂梅聪騻鞑ニ惴ǖ牡胤健７聪騻鞑ニ惴ǖ暮诵募磳?duì)整個(gè)網(wǎng)絡(luò)所有可能的路徑重復(fù)使用鏈?zhǔn)椒▌t。反向傳播算法真正強(qiáng)大的地方在于它是動(dòng)態(tài)規(guī)劃的，我們可以重復(fù)使用中間結(jié)果計(jì)算梯度下降。因?yàn)樗峭ㄟ^(guò)神經(jīng)網(wǎng)絡(luò)由后向前傳播誤差，并優(yōu)化每一個(gè)神經(jīng)節(jié)點(diǎn)之間的權(quán)重，所以這種算法就稱之為反向傳播算法（backpropagation algorithm）。實(shí)際上神經(jīng)網(wǎng)絡(luò)反向傳播與前向傳播有緊密的聯(lián)系，只不過(guò)反向傳播算法不是通過(guò)神經(jīng)網(wǎng)絡(luò)由前向后傳播數(shù)據(jù)，而是由后向前傳播誤差。

大多數(shù)反向傳播算法的解釋都是直接從一般理論推導(dǎo)開(kāi)始，但是如果從手動(dòng)計(jì)算梯度開(kāi)始，那么就能很自然地推導(dǎo)出反向傳播算法本身。雖然下面的推導(dǎo)部分較長(zhǎng)，但我們認(rèn)為從數(shù)學(xué)基本理論開(kāi)始是較好的方式來(lái)了解反向傳播算法。

下文由單路徑神經(jīng)網(wǎng)絡(luò)開(kāi)始，進(jìn)而推廣到存在多層和多個(gè)神經(jīng)元的神經(jīng)網(wǎng)絡(luò)，最后再推導(dǎo)出一般的反向傳播算法。

反向傳播算法的基本原則

我們訓(xùn)練神經(jīng)網(wǎng)絡(luò)的最終目標(biāo)是尋找損失函數(shù)關(guān)于每一個(gè)權(quán)重的梯度：

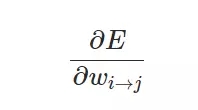
當(dāng)我們計(jì)算出偏導(dǎo)數(shù)時(shí)就能進(jìn)一步使用隨機(jī)梯度下降或小批量梯度下降更新每一層神經(jīng)網(wǎng)絡(luò)的權(quán)重：

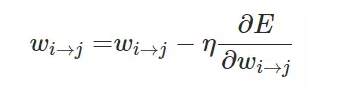
通常在一般神經(jīng)網(wǎng)絡(luò)的每一個(gè)單元會(huì)存在以下幾種情況：

該神經(jīng)元有且僅有一個(gè)輸入和一個(gè)輸出

該神經(jīng)元有多個(gè)輸入

該神經(jīng)元有多個(gè)輸出

該神經(jīng)元有多個(gè)輸入和輸出

因?yàn)槎噍斎肱c多輸出是獨(dú)立的，我們能自由組合輸入與輸出神經(jīng)元的數(shù)量。

這一部分將從相對(duì)簡(jiǎn)單的結(jié)構(gòu)到多層神經(jīng)網(wǎng)絡(luò)，并在這個(gè)過(guò)程中推導(dǎo)出用于反向傳播的一般規(guī)則。最后，我們會(huì)將這些規(guī)則組合成可用于任意神經(jīng)網(wǎng)絡(luò)的反向傳播算法。

單一輸入與單一輸出的神經(jīng)元

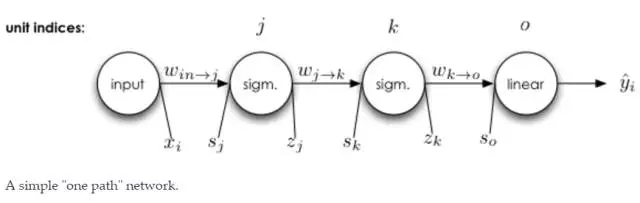
在上面的神經(jīng)網(wǎng)絡(luò)中，每一個(gè)變量都能夠準(zhǔn)確地寫(xiě)出來(lái)。

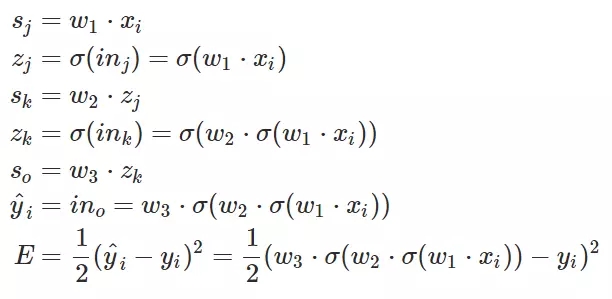
注意，上面方程式中 x 是輸入，w 是權(quán)重，Sigamm 是神經(jīng)元的激活函數(shù)。s 是前一個(gè)神經(jīng)元通過(guò)權(quán)重傳遞到后一個(gè)神經(jīng)元的數(shù)據(jù)，它等于前一個(gè)神經(jīng)元的輸出乘以兩個(gè)神經(jīng)元的連接強(qiáng)度，即權(quán)重 w。z 是神經(jīng)元輸入經(jīng)過(guò)激活函數(shù) Sigamma 計(jì)算后得到的輸出。

E 就相當(dāng)于系統(tǒng)做出的判斷與正確標(biāo)注之間的損失。E 對(duì)權(quán)重 w 求偏導(dǎo)并最小化，即在損失函數(shù) E 最小的情況下求得權(quán)重 w，上述方程式表明需要求得 k 神經(jīng)元到 o 神經(jīng)元之間最優(yōu)權(quán)重 w。

那么從 j 到 k 和從 i 到 j 的權(quán)重更新都是相同的步驟了。

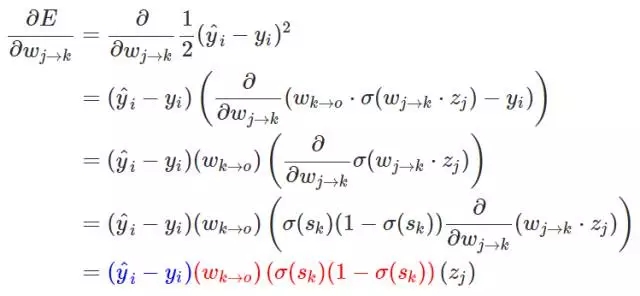
上面的推導(dǎo)表達(dá)式展示了損失函數(shù)對(duì)第 j 層和第 k 層之間權(quán)重的偏導(dǎo)數(shù)，而下面的推導(dǎo)表達(dá)式則展示了損失函數(shù)對(duì)第 i 層和第 j 層之間權(quán)重的偏導(dǎo)數(shù)：

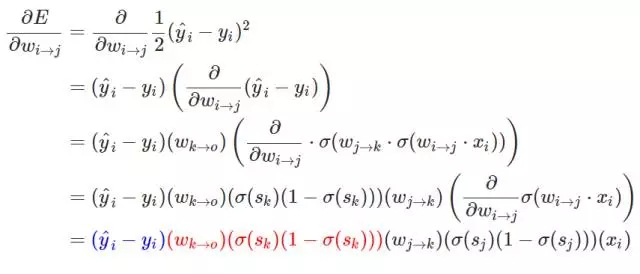
現(xiàn)在也許我們能總結(jié)一個(gè)可以使用反向傳播算法的權(quán)重更新模式。當(dāng)我們計(jì)算神經(jīng)網(wǎng)絡(luò)前面層級(jí)的權(quán)重更新時(shí)，我們重復(fù)使用了多個(gè)數(shù)值。具體來(lái)說(shuō)，我們觀察到的就是神經(jīng)網(wǎng)絡(luò)損失函數(shù)的偏導(dǎo)數(shù)，上面三個(gè)推導(dǎo)表達(dá)式可以總結(jié)為：

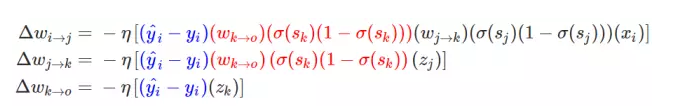
在上述方程式中由后一個(gè)神經(jīng)元向前推導(dǎo)，最后一層的權(quán)重更新梯度最簡(jiǎn)單，而前面層級(jí)的更新梯度則需要向前推導(dǎo)，這一推導(dǎo)的過(guò)程或者方式就是根據(jù)求導(dǎo)的鏈?zhǔn)椒▌t。

多個(gè)輸入

可以思考一下稍微復(fù)雜一點(diǎn)的神經(jīng)網(wǎng)絡(luò)，即一個(gè)神經(jīng)元將有多個(gè)輸入：

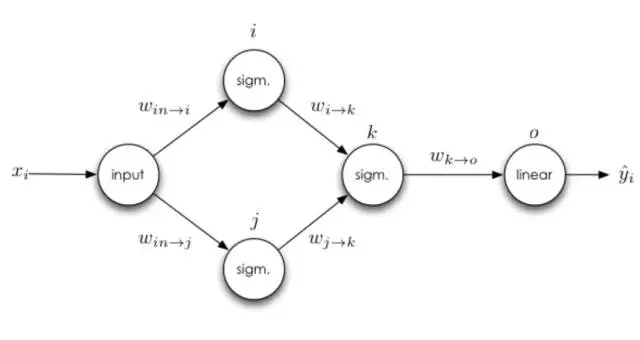
如果一個(gè)神經(jīng)元有多個(gè)輸入端怎么辦，從 j 到 k 的權(quán)重更新規(guī)則會(huì)不會(huì)影響從 i 到 k 的權(quán)重更新規(guī)則？為了弄清這個(gè)問(wèn)題，我們可以對(duì) i 到 k 的權(quán)重手動(dòng)求導(dǎo)。

我們可以從上面看到從 i 到 k 的權(quán)重更新是不依賴于從 j 到 k 權(quán)重的導(dǎo)數(shù)的，因此第一條準(zhǔn)測(cè)就是損失函數(shù)對(duì)權(quán)重的導(dǎo)數(shù)不依賴于同層級(jí)神經(jīng)網(wǎng)絡(luò)上的其他任何權(quán)重的導(dǎo)數(shù)，所以神經(jīng)網(wǎng)絡(luò)同層級(jí)的權(quán)重可以獨(dú)立地更新。同時(shí)該法則還存在更新的自然順序，這種自然順序僅僅只依賴于神經(jīng)網(wǎng)絡(luò)同一層級(jí)其他權(quán)重的值，這種排序是反向傳播算法的計(jì)算基礎(chǔ)。

多個(gè)輸出

接下來(lái)我們可以思考下有多個(gè)輸出的隱藏層神經(jīng)元。

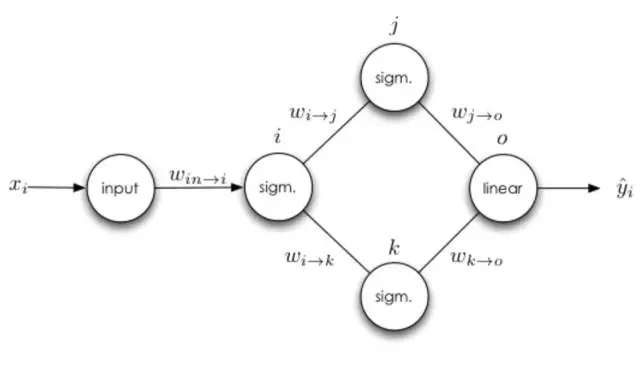
在前面的基礎(chǔ)上，和前面權(quán)重更新有差別的是輸入神經(jīng)元與 i 神經(jīng)元之間的求導(dǎo)法則。神經(jīng)元多輸出端的情況就是其有多個(gè)直接后繼神經(jīng)元，所以我們必須沿著以神經(jīng)元 i 為根結(jié)點(diǎn)的所有路徑來(lái)計(jì)算誤差的總和。接下來(lái)我們可以詳細(xì)地寫(xiě)出損失函數(shù)對(duì)權(quán)重求導(dǎo)而更新的過(guò)程，并且我們定義σ(?) 就是神經(jīng)元 i 的激活函數(shù)：

現(xiàn)在有兩點(diǎn)需要注意，首先就是第二條推導(dǎo)準(zhǔn)則：具有多個(gè)輸出的神經(jīng)元權(quán)重更新依賴于所有可能路徑上的導(dǎo)數(shù)。

但是更重要地是我們需要看到反向傳播算法和正向傳播算法之間的聯(lián)系。在反向傳播的過(guò)程中，我們會(huì)計(jì)算神經(jīng)網(wǎng)絡(luò)輸出端的誤差，我們會(huì)把這些誤差反向傳播并且沿著每條路徑加權(quán)。當(dāng)我們傳播到了一個(gè)神經(jīng)元，可以將經(jīng)權(quán)重反向傳播過(guò)來(lái)的誤差乘以神經(jīng)元的導(dǎo)數(shù)，然后就可以同樣的方式反向傳播誤差，一直追溯到輸入端。反向傳播非常類似于正向傳播，是一種遞歸算法。接下來(lái)會(huì)介紹誤差信號(hào)，然后再改寫(xiě)我們的表達(dá)式。

誤差信號(hào)

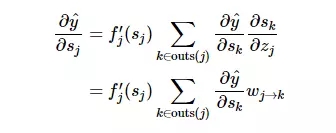
現(xiàn)在我們能用緊湊的方程式表征反向傳播誤差。

反向傳播算法的普遍形式

先回憶下第一部分的簡(jiǎn)單神經(jīng)網(wǎng)絡(luò):

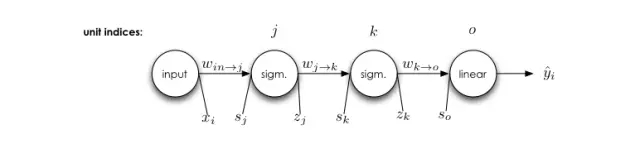
我們能使用 δ_i 的定義導(dǎo)出整個(gè)神經(jīng)網(wǎng)絡(luò)的所有誤差信號(hào)：

在這一個(gè)神經(jīng)網(wǎng)絡(luò)中，準(zhǔn)確的權(quán)重更新模式是以下方程式：

還有另外一個(gè)復(fù)雜一點(diǎn)的神經(jīng)網(wǎng)絡(luò)，即有多個(gè)輸出神經(jīng)元：

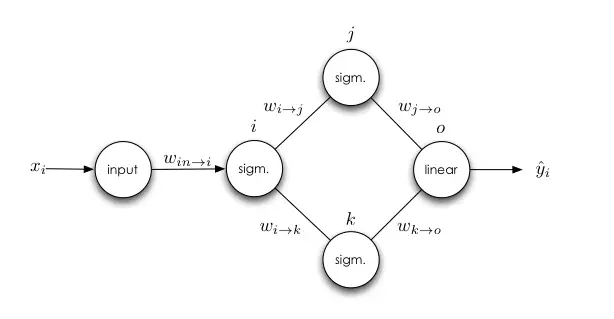
同樣我們能得出所有的誤差信號(hào)：

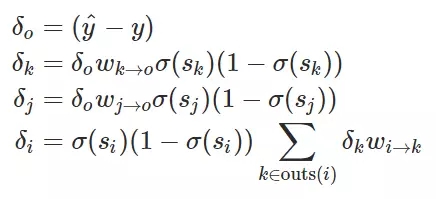
然后我們?cè)僖淮螌⒄`差代入到權(quán)重更新方程式中：

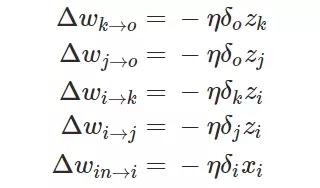
現(xiàn)在也許我們就可以推導(dǎo)出權(quán)重更新的簡(jiǎn)單通用形式：

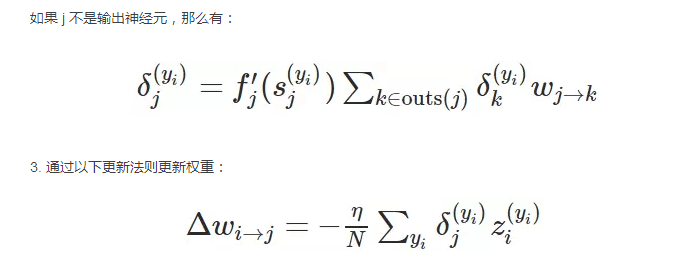
上面是一般反向傳播算法的推導(dǎo)和建立過(guò)程，我們從最簡(jiǎn)單與直覺(jué)的概念一步步完善并推導(dǎo)出最后的更新規(guī)則。雖然反向傳播算法有著很多的局限性與不足，并且也有學(xué)者提出如解耦方法等理論解決反向傳播算法的不足，但反向傳播算法仍然是目前神經(jīng)網(wǎng)絡(luò)中最主流與強(qiáng)大的最優(yōu)化方法。最后我們同樣期待 Hinton 等人所提出的capsule能對(duì)反向傳播算法有本質(zhì)上的提升！

原文鏈接：

https://medium.com/intuitionmachine/the-deeply-suspicious-nature-of-backpropagation-9bed5e2b085e

http://briandolhansky.com/blog/2013/9/27/artificial-neural-networks-backpropagation-part-4

商業(yè)智能與數(shù)據(jù)分析群

興趣范圍包括各種讓數(shù)據(jù)產(chǎn)生價(jià)值的辦法，實(shí)際應(yīng)用案例分享與討論，分析工具，ETL工具，數(shù)據(jù)倉(cāng)庫(kù)，數(shù)據(jù)挖掘工具，報(bào)表系統(tǒng)等全方位知識(shí)

QQ群：81035754