小編寫這篇文章的主要目的，主要是給大家做一個詳細的介紹，介紹的內容是Python可視化神器，這個神器指的是pyecharts，那么，怎么樣利用這種語言去進行繪制箱型圖呢？下面小編就給大家詳細解答下。

　　概念

　　后面的圖形都是一些專業的統計圖形，當然也會是我們可視化的對象。

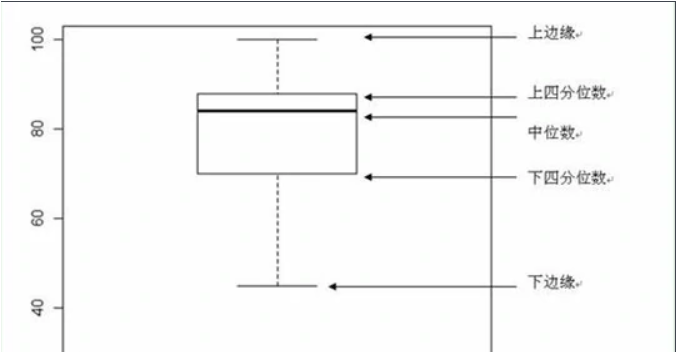
　　箱形圖（Box-plot）又稱為盒須圖、盒式圖或箱線圖，是一種用作顯示一組數據分散情況資料的統計圖。因形狀如箱子而得名。在各種領域也經常被使用，常見于品質管理。它主要用于反映原始數據分布的特征，還可以進行多組數據分布特征的比較。箱線圖的繪制方法是：先找出一組數據的上邊緣、下邊緣、中位數和兩個四分位數；然后，連接兩個四分位數畫出箱體；再將上邊緣和下邊緣與箱體相連接，中位數在箱體中間。

　　用處

　　1.直觀明了地識別數據批中的異常值

　　上文講了很久的識別異常值，其實箱線圖判斷異常值的標準以四分位數和四分位距為基礎，四分位數具有一定的耐抗性，多達25%的數據可以變得任意遠而不會很大地擾動四分位數，所以異常值不會影響箱形圖的數據形狀，箱線圖識別異常值的結果比較客觀。由此可見，箱線圖在識別異常值方面有一定的優越性。

　　2.利用箱線圖判斷數據批的偏態和尾重

　　對于標準正態分布的樣本，只有極少值為異常值。異常值越多說明尾部越重，自由度越小（即自由變動的量的個數）；

　　而偏態表示偏離程度，異常值集中在較小值一側，則分布呈左偏態；異常值集中在較大值一側，則分布呈右偏態。

　　3.利用箱線圖比較幾批數據的形狀

　　同一數軸上，幾批數據的箱線圖并行排列，幾批數據的中位數、尾長、異常值、分布區間等形狀信息便昭然若揭。如上圖，可直觀得看出第三季度各分公司的銷售額大體都在下降。

　　箱形圖系列模板

　　第一個箱形圖

　　說實話這類圖形的繪制，如果不懂專業的知識可能也無法理解，對于如何深層次的理解這個圖形的具體含義，請移步到其他專欄，我會詳細介紹，這里就不做過多的解釋了。

　　from pyecharts import options as opts
　　from pyecharts.charts import Boxplot
　　v1=[
　　[850,740,900,1070,930,850,950,980,980,880,1000,980],
　　[960,940,960,940,880,800,850,880,900,840,830,790],
　　]
　　v2=[
　　[890,810,810,820,800,770,760,740,750,760,910,920],
　　[890,840,780,810,760,810,790,810,820,850,870,870],
　　]
　　c=Boxplot()
　　c.add_xaxis(["expr1","expr2"])
　　c.add_yaxis("A",c.prepare_data(v1))
　　c.add_yaxis("B",c.prepare_data(v2))
　　c.set_global_opts(title_opts=opts.TitleOpts(title="標題"))
　　c.render("簡單示例.html")
　　print(c.prepare_data(v1))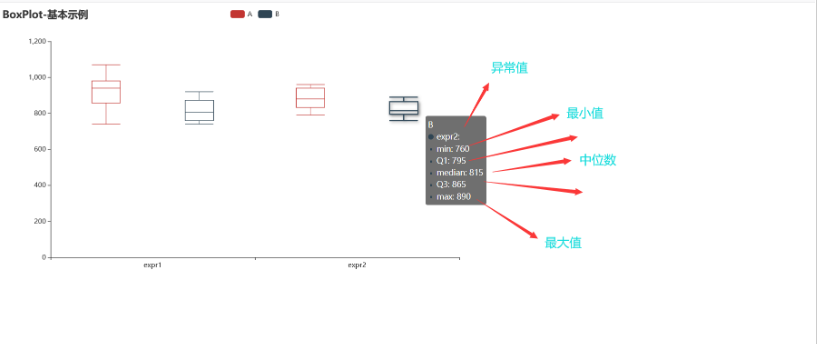

   　復雜一點的圖例

　　import pyecharts.options as opts
　　from pyecharts.charts import Grid,Boxplot,Scatter
　　y_data=[
　　[
　　850,
　　740,
　　900,
　　1070,
　　930,
　　850,
　　950,
　　980,
　　980,
　　880,
　　1000,
　　980,
　　930,
　　650,
　　760,
　　810,
　　1000,
　　1000,
　　960,
　　960,
　　],
　　[
　　960,
　　940,
　　960,
　　940,
　　880,
　　800,
　　850,
　　880,
　　900,
　　840,
　　830,
　　790,
　　810,
　　880,
　　880,
　　830,
　　800,
　　790,
　　760,
　　800,
　　],
　　[
　　880,
　　880,
　　880,
　　860,
　　720,
　　720,
　　620,
　　860,
　　970,
　　950,
　　880,
　　910,
　　850,
　　870,
　　840,
　　840,
　　850,
　　840,
　　840,
　　840,
　　],
　　[
　　890,
　　810,
　　810,
　　820,
　　800,
　　770,
　　760,
　　740,
　　750,
　　760,
　　910,
　　920,
　　890,
　　860,
　　880,
　　720,
　　840,
　　850,
　　850,
　　780,
　　],
　　[
　　890,
　　840,
　　780,
　　810,
　　760,
　　810,
　　790,
　　810,
　　820,
　　850,
　　870,
　　870,
　　810,
　　740,
　　810,
　　940,
　　950,
　　800,
　　810,
　　870,
　　],
　　]
　　scatter_data=[650,620,720,720,950,970]
　　box_plot=Boxplot()
　　box_plot=(
　　box_plot.add_xaxis(xaxis_data=["expr 0","expr 1","expr 2","expr 3","expr 4"])
　　.add_yaxis(series_name="",y_axis=box_plot.prepare_data(y_data))
　　.set_global_opts(
　　title_opts=opts.TitleOpts(
　　pos_left="center",title="Michelson-Morley Experiment"
　　),
　　tooltip_opts=opts.TooltipOpts(trigger="item",axis_pointer_type="shadow"),
　　xaxis_opts=opts.AxisOpts(
　　type_="category",
　　boundary_gap=True,
　　splitarea_opts=opts.SplitAreaOpts(is_show=False),
　　axislabel_opts=opts.LabelOpts(formatter="expr{value}"),
　　splitline_opts=opts.SplitLineOpts(is_show=False),
　　),
　　yaxis_opts=opts.AxisOpts(
　　type_="value",
　　name="km/s minus 299,000",
　　splitarea_opts=opts.SplitAreaOpts(
　　is_show=True,areastyle_opts=opts.AreaStyleOpts(opacity=1)
　　),
　　),
　　)
　　.set_series_opts(tooltip_opts=opts.TooltipOpts(formatter="{b}:{c}"))
　　)
　　scatter=(
　　Scatter()
　　.add_xaxis(xaxis_data=["expr 0","expr 1","expr 2","expr 3","expr 4"])
　　.add_yaxis(series_name="",y_axis=scatter_data)
　　.set_global_opts(
　　title_opts=opts.TitleOpts(
　　pos_left="10%",
　　pos_top="90%",
　　title="upper:Q3+1.5*IQRnlower:Q1-1.5*IQR",
　　title_textstyle_opts=opts.TextStyleOpts(
　　border_color="#999",border_width=1,font_size=14
　　),
　　),
　　yaxis_opts=opts.AxisOpts(
　　axislabel_opts=opts.LabelOpts(is_show=False),
　　axistick_opts=opts.AxisTickOpts(is_show=False),
　　),
　　)
　　)
　　grid=(
　　Grid(init_opts=opts.InitOpts(width="1200px",height="600px"))
　　.add(
　　box_plot,
　　grid_opts=opts.GridOpts(pos_left="10%",pos_right="10%",pos_bottom="15%"),
　　)
　　.add(
　　scatter,
　　grid_opts=opts.GridOpts(pos_left="10%",pos_right="10%",pos_bottom="15%"),
　　)
　　.render("第一個箱形圖.html")
　　)

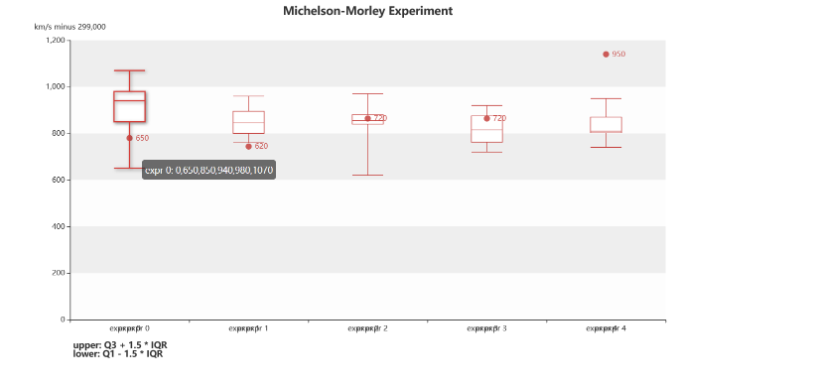
　　其實對于這個圖形的繪制我個人覺得掌握好一定技巧，繪制圖形并不難，主要是你要知道一定數據分析方法，不然空談數據可視也是枉然。

　　綜上所述，這篇文章就給大家介紹到這里了，希望可以給大家帶來更多幫助。