對(duì)于很多從事Python的人來(lái)說(shuō)，有很多的人想要去進(jìn)階的，比如學(xué)習(xí)跟多的一些知識(shí)，比如，我們?cè)诠ぷ髦袝?huì)遇到，使用Python計(jì)算AUC的三種方式，下面給大家做出一個(gè)解答。

　　介紹

　　AUC（Area Under Curve），其實(shí)就是ROC曲線圍成的和下坐標(biāo)軸圍成的一個(gè)面積，這個(gè)面積的數(shù)值一般是不會(huì)大于1的。

　　當(dāng)然，ROC曲線基本上都在y=x，這條直線上面的一個(gè)正上方，因此AUC的正確值應(yīng)該在在0.5和1之間。AUC越接近1，它檢測(cè)出來(lái)的值就是越真實(shí)的;等于0.5時(shí)，它的真實(shí)性是最低了，當(dāng)然也沒(méi)有任何的相關(guān)參考價(jià)值。

　　實(shí)現(xiàn)代碼

　　import numpy as np
　　from sklearn.metrics import roc_auc_score
　　y_true=[1,1,0,0,1,1,0]
　　y_pred=[0.8,0.7,0.5,0.5,0.5,0.5,0.3]
　　print(roc_auc_score(y_true,y_pred))
　　#下面實(shí)現(xiàn)的是方法1
　　#https://blog.csdn.net/lieyingkub99/article/details/81266664?utm_medium=distribute.pc_relevant.none-task-blog-title-1&spm=1001.2101.3001.4242
　　def cal_auc1(y_true,y_pred):
　　n_bins=10
　　postive_len=sum(y_true)#M正常樣本測(cè)試個(gè)數(shù)
　　negative_len=len(y_true)-postive_len#N負(fù)樣本數(shù)測(cè)試個(gè)數(shù)
　　total_case=postive_len*negative_len#M*N樣本對(duì)數(shù)
　　pos_histogram=[0 for _ in range(n_bins)]#保存每一個(gè)概率值下的正常樣本個(gè)數(shù)
　　neg_histogram=[0 for _ in range(n_bins)]#保存每一個(gè)概率值下的負(fù)樣本個(gè)數(shù)
　　bin_width=1.0/n_bins
　　for i in range(len(y_true)):
　　nth_bin=int(y_pred<i>/bin_width)#概率值轉(zhuǎn)化為整數(shù)下標(biāo)
　　if y_true<i>==1:
　　pos_histogram[nth_bin]+=1
　　else:
　　neg_histogram[nth_bin]+=1
　　print(pos_histogram)
　　print(neg_histogram)
　　accumulated_neg=0
　　satisfied_pair=0
　　for i in range(n_bins):
　　satisfied_pair+=(pos_histogram<i>*accumulated_neg+pos_histogram<i>*neg_histogram<i>*0.5)
　　print(pos_histogram<i>,neg_histogram<i>,accumulated_neg,satisfied_pair)
　　accumulated_neg+=neg_histogram<i>
　　return satisfied_pair/float(total_case)
　　print(cal_auc1(y_true,y_pred))
　　#下面實(shí)現(xiàn)的是方法2
　　#https://blog.csdn.net/lieyingkub99/article/details/81266664?utm_medium=distribute.pc_relevant.none-task-blog-title-1&spm=1001.2101.3001.4242
　　def cal_auc2(y_true,y_pred):
　　n_bins=10
　　postive_len=sum(y_true)#M正樣本個(gè)數(shù)
　　negative_len=len(y_true)-postive_len#N負(fù)樣本個(gè)數(shù)
　　total_case=postive_len*negative_len#M*N樣本對(duì)數(shù)
　　prob_rank=[0 for _ in range(n_bins)]#保存每一個(gè)概率值的rank
　　prob_num=[0 for _ in range(n_bins)]#保存每一個(gè)概率值出現(xiàn)的次數(shù)
　　bin_width=1.0/n_bins
　　raw_arr=[]
　　for i in range(len(y_true)):
　　raw_arr.append([y_pred<i>,y_true<i>])
　　arr=sorted(raw_arr,key=lambda d:d[0])#按概率由低到高排序
　　for i in range(len(arr)):
　　nth_bin=int(arr<i>[0]/bin_width)#概率值轉(zhuǎn)化為整數(shù)下標(biāo)
　　prob_rank[nth_bin]=prob_rank[nth_bin]+i+1
　　prob_num[nth_bin]=prob_num[nth_bin]+1
　　satisfied_pair=0
　　for i in range(len(arr)):
　　if arr<i>[1]==1:
　　nth_bin=int(arr<i>[0]/bin_width)#概率值轉(zhuǎn)化為整數(shù)下標(biāo)
　　satisfied_pair=satisfied_pair+prob_rank[nth_bin]/prob_num[nth_bin]
　　return(satisfied_pair-postive_len*(postive_len+1)/2)/total_case
　　print(cal_auc2(y_true,y_pred))
　　#根據(jù)roc曲線,找不同點(diǎn)算下面積,需要點(diǎn)足夠多
　　def cal_auc3(y_true,y_pred):
　　"""Summary
　　Args:
　　raw_arr(TYPE):Description
　　Returns:
　　TYPE:Description
　　"""
　　raw_arr=[]
　　for i in range(len(y_true)):
　　raw_arr.append([y_pred<i>,y_true<i>])
　　print(raw_arr)
　　arr=sorted(raw_arr,key=lambda d:d[0],reverse=True)
　　pos,neg=0.,0.
　　for record in arr:
　　if record[1]==1.:
　　pos+=1
　　else:
　　neg+=1
　　fp,tp=0.,0.
　　xy_arr=[]
　　for record in arr:
　　if record[1]==1.:
　　tp+=1
　　else:
　　fp+=1
　　xy_arr.append([fp/neg,tp/pos])
　　print(xy_arr)
　　auc=0.
　　prev_x=0.
　　prev_y=0.
　　for x,y in xy_arr:
　　if x!=prev_x:
　　auc+=((x-prev_x)*(y+prev_y)/2.)
　　prev_x=x
　　prev_y=y
　　print(auc)
　　import numpy as np
　　from sklearn.metrics import roc_auc_score
　　y_true=[1,1,0,0,1,1,0]
　　y_pred=[0.8,0.7,0.5,0.5,0.5,0.5,0.3]
　　print(roc_auc_score(y_true,y_pred))

　　方法補(bǔ)充

　　另外還有不同的方法，它們會(huì)各自輸出各自的auc，這樣我們就可以用來(lái)對(duì)其進(jìn)行計(jì)算面積，去實(shí)現(xiàn)其相關(guān)的功能。

　　在通過(guò)面積計(jì)算AUC的方法中，沒(méi)有遍歷數(shù)據(jù)的預(yù)測(cè)概率作為分類閾值，而是對(duì)[0,1]區(qū)間等分得到一系列閾值。

#AUC的計(jì)算
　　import numpy as np
　　import matplotlib.pyplot as plt
　　for e in range(3):
　　print("nRound:",e+1)
　　num=1000
　　auc1=auc2=auc3=0.
　　#準(zhǔn)備數(shù)據(jù)
　　pred_prob=list(np.random.uniform(low=0,high=1,size=[num]))
　　labels=[int(prob>0.5)for prob in list(np.random.uniform(low=0,high=1,size=[num]))]
　　#檢查數(shù)據(jù)
　　#print("pred_prob:n",pred_prob)
　　#print("labels:n",labels)
　　#方法一，面積加和
　　roc_point=[]
　　for i in range(num):
　　i=pred_prob<i>
　　TP=0#真陽(yáng)樣本數(shù)
　　FP=0#假陽(yáng)樣本數(shù)
　　TP_rate=0.#真陽(yáng)率
　　FP_rate=0.#假陽(yáng)率
　　pos_num=0#預(yù)測(cè)真樣本數(shù)
　　#計(jì)數(shù)過(guò)程
　　for ind,prob in enumerate(pred_prob):
　　if prob>i:
　　pos_num+=1
　　if prob>i and labels[ind]>0.5:
　　TP+=1
　　elif prob>i and labels[ind]<0.5:
　　FP+=1
　　if pos_num!=0:
　　TP_rate=TP/sum(labels)
　　FP_rate=FP/(num-sum(labels))
　　roc_point.append([FP_rate,TP_rate])#記錄ROC中的點(diǎn)
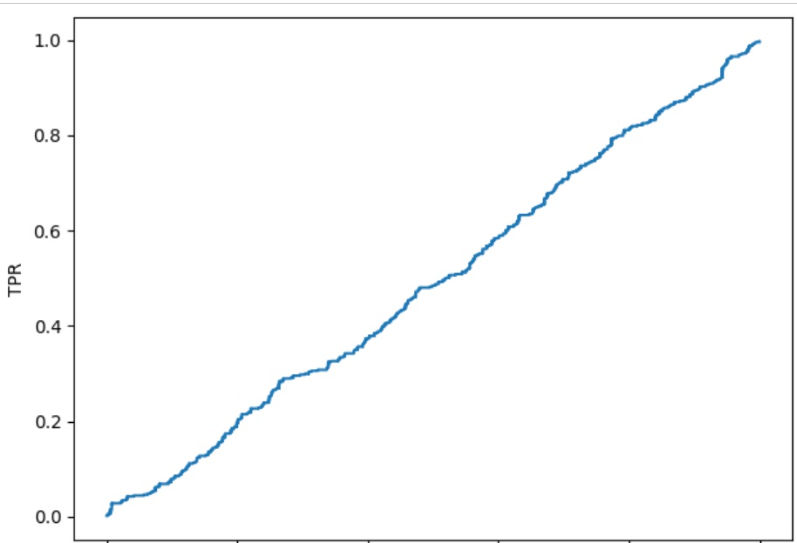
　　#畫出ROC曲線
　　roc_point.sort(key=lambda x:x[0])
　　plt.plot(np.array(roc_point)[1:,0],np.array(roc_point)[1:,1])
　　plt.xlabel("FPR")
　　plt.ylabel("TPR")
　　plt.show()
　　#計(jì)算每個(gè)小長(zhǎng)方形的面積，求和即為auc
　　lastx=0.
　　for x,y in roc_point:
　　auc1+=(x-lastx)*y#底乘高
　　lastx=x
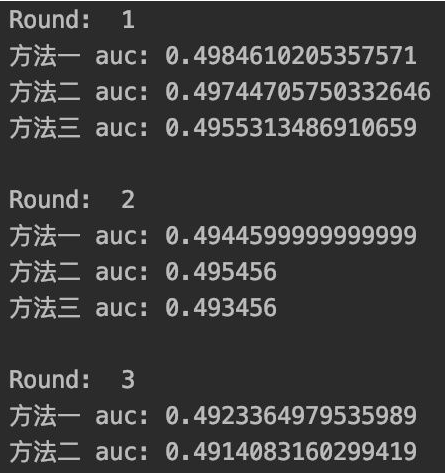
　　print("方法一auc:",auc1)
　　#方法二，利用AUC關(guān)于排列概率的定義計(jì)算
　　auc2=0
　　P_ind=[]#正樣本下標(biāo)
　　F_ind=[]#負(fù)樣本下標(biāo)
　　P_F=0#正樣本分?jǐn)?shù)高于負(fù)樣本的數(shù)量
　　F_P=0#負(fù)樣本分?jǐn)?shù)高于正樣本的數(shù)量
　　#計(jì)數(shù)過(guò)程
　　for ind,val in enumerate(labels):
　　if val>0.5:
　　P_ind.append(ind)
　　else:
　　F_ind.append(ind)
　　for Pi in P_ind:
　　for Fi in F_ind:
　　if pred_prob[Pi]>pred_prob[Fi]:
　　P_F+=1
　　else:
　　F_P+=1
　　auc2=P_F/(len(P_ind)*len(F_ind))
　　print("方法二auc:",auc2)
　　#方法三，方法二的改進(jìn)，簡(jiǎn)化了計(jì)算，降低了時(shí)間復(fù)雜度
　　new_data=[[p,l]for p,l in zip(pred_prob,labels)]
　　new_data.sort(key=lambda x:x[0])
　　#求正樣本rank之和
　　rank_sum=0
　　for ind,[prob,label]in enumerate(new_data):
　　if label>0.5:
　　rank_sum+=ind
　　auc3=(rank_sum-len(P_ind)*(1+len(P_ind))/2)/(len(P_ind)*len(F_ind))
　　print("方法三auc:",auc3)

　　運(yùn)行結(jié)果

　　上面關(guān)于Python計(jì)算AUC的三種方式就為大家介紹到這里了，希望能夠各位讀者帶來(lái)幫助。