摘要：但在年春季關于理論機器學習的課程上，泛化理論專家表達了對這篇論文的不滿，尤其是其標題。在一個相關的說明中，及其聯合作者的幾篇更早期的論文已經提出了與張弛原等人對深度網絡的看法相當相似的觀點。

深度學習的理論還存在諸多神秘之處。近來很多機器學習理論研究者都在關注神秘的泛化（generalization）：為什么訓練后的深度網絡能在之前并未見過的數據上取得良好的表現，即便它們的自由參數的數量遠遠超過了數據點的數量（經典的「過擬合」情況）？張馳原等人的論文《理解深度學習需要重新思考泛化（Understanding Deep Learning requires Rethinking Generalization）》為這一難題帶來了一些關注。

論文地址：https://arxiv.org/abs/1611.03530。

他們的主要實驗發現是：如果你在帶有隨機標簽的圖像上訓練一個經典的卷積網絡架構（比如 Alexnet），那么你仍然可以在這些訓練數據上實現非常高的準確度。（此外，人們認為有助于實現更好的泛化的常見正則化策略其實幫助不大。）不用說，這個訓練后的網絡之后并不能預測仍未見過的圖像的（隨機）標簽，這就意味著它不能泛化。這篇論文指出將分類器與帶有隨機標簽的數據進行擬合的能力也是機器學習領域內的一種傳統方法，該方法被稱為 Rademacher 復雜度（后面我們會討論），因此 Rademacher 復雜度在樣本復雜度上并沒有有意義的邊界。我覺得這篇論文寫得很有意思，推薦閱讀。該論文獲得了 ICLR 2017 較佳論文獎，恭喜作者。

但在 2017 年春季關于理論機器學習的 Simons Institute 課程上，泛化理論專家表達了對這篇論文的不滿，尤其是其標題。他們認為相似的問題已經在更簡單的模型上得到過廣泛的研究了，比如 kernel SVM（核支持向量機）（老實說，這篇論文里也明確提到過）。設計具有很高 Rademacher 復雜度同時又能在真實數據上很好地訓練和泛化的支持向量機架構是很簡單的。此外，用于解釋這種泛化行為的理論也已經得到了發展（而且還適用于 boosting 等相關模型）。在一個相關的說明中，Behnam Neyshabur 及其聯合作者的幾篇更早期的論文已經提出了與張弛原等人對深度網絡的看法相當相似的觀點。

但不管這些吐槽抱怨，張弛原等人的論文讓人們關注起這個核心的理論難題了，我們應該感到高興。實際上，在 Simons Institute 課程上的熱情討論者自己也組成了小組來解決這個難題，這帶來了多篇論文（其中后兩篇出現在了 NIPS" 17 上）：

Dzigaite 和 Roy 的論文《Computing Nonvacuous Generalization Bounds for Deep (Stochastic) Neural Networks with Many More Parameters than Training Data》：https://arxiv.org/abs/1703.11008

Bartlett、Foster 和 Telgarsky 的論文《Spectrally-normalized margin bounds for neural networks》https://arxiv.org/abs/1706.08498

Neyshabur、Bhojapalli、MacAallester 和 Srebro 的論文《A PAC-Bayesian Approach to Spectrally-Normalized Margin Bounds for Neural Networks》：https://arxiv.org/abs/1707.09564

在解讀這些研究結果之前，我先說明一下對張弛原等人論文的標題的部分爭議源自一些基本的困惑，即當前的泛化理論是規范性的還是僅僅是描述性的。這些困惑由源自課程和教科書對泛化理論的標準對待方式，我在我的研究生課程上教授最近的進展時也發現了這一點。

規范性理論還是描述性理論

為了闡釋兩者的差異，假設有一位病人對其醫生說：「醫生，我晚上常常醒來而且一天都很累。」

醫生 1（沒有進行任何身體檢查）：「哦，你患了失眠癥。」

我將這種診斷稱為描述性的（descriptive），因為這只是給該病人的問題分配一個標簽，而沒有給出如何解決該問題的任何見解。與之相反：

醫生 2（經過仔細的身體檢查后）：「你的鼻竇增生導致睡眠呼吸暫停。移除它可以解決你的問題。」

這樣的診斷是規范性的（prescriptive）。

泛化理論：描述性還是規范性？

比如 VC 維、Rademacher 復雜度和 PAC-Bayes 邊界等泛化理論概念是為缺乏泛化的基本現象賦予一個描述性標簽。對于今天復雜的機器學習模型來說，它們很難計算，更不要說用來指導學習系統的設計了。

泛化理論：描述性部分

我們現在討論 Rademacher 復雜度，本文中的討論會有所簡化。詳情可參閱我的課程筆記：https://www.cs.princeton.edu/courses/archive/fall17/cos597A/lecnotes/generalize.pdf。在這里的討論中，為了方便起見，假設標簽和損失是 0 和 1，并且假設泛化能力糟糕的 h 在訓練樣本 S 上的表現完美但在留存集 S2 上的完全錯誤，也就是說：

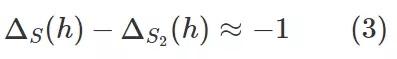
Rademacher 復雜度涉及到下面的思想實驗。從 D 中取大小為 2m 的單個樣本集，然后將其分成兩半，其中一半是 S，另一半是 S2。翻轉 S2 中點的標簽。現在嘗試尋找能較好地描述這些新樣本的分類器 C，也就是說最小化

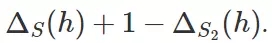
為什么呢？因為翻轉點的標簽可以將好的分類變成糟糕的分類，或反過來，因此 S2 的損失函數是 1 減去翻轉前的損失。如果這個量有很高的概率很小（比如接近于 0），那么我們就說這個分類器的類別的 Rademacher 復雜度高。

但 (3) 式表明 Rademacher 復雜度高的情況是：S、S2 是來自 D 的大小為 m 的隨機樣本，所以它們的總大小是 2m；當泛化失敗時，我們就成功找到了使

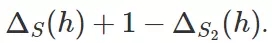
非常小的假設 h。

換句話說，繼續用醫療的例子類比，醫生只需聽到「泛化沒有發生」就得到結論「Rademacher 復雜度高」。所以我說這個結果是描述性的。

類似地，VC 維邊界也是描述性的。如果存在一個大小為 k 的集合使得下面的結果成立，那么 VC 維至少是 k+1。如果我們檢查類別中的所有可能的分類器，并且該標簽序列中每一個標簽都給了樣本中的 k 個數據點，那么我們可以找到 0 和 1 構成的所有可能的 2^k 個序列。

因此，再次類比一下，醫生只需聽到「泛化沒有在樣本大小為 m 的情況下實現」就得到結論「VC 維高于Ω(m/logm)」。

我們也可以類似地證明 PAC-Bayes 邊界也是描述性的，你可以在我的課程筆記中看到：http://www.cs.princeton.edu/courses/archive/fall17/cos597A/lecnotes/generalize.pdf

為什么學生搞不清楚，認為這樣的泛化理論工具能為機器學習算法的設計提供一些強有力的技術呢？

答案：也許是因為教學筆記和教科書中的標準演示就像是在假設我們在計算上是萬能的——好像我們可以計算 VC 維和 Rademacher 復雜度并因此能在可實現泛化的訓練所需的樣本規模上達到有意義的邊界。盡管之前在使用簡單的分類器的時候也許能辦到，但現在我們的復雜分類器具有數以百萬計的變量，而且這些變量還是反向傳播等非凸優化技術的產物。為了降低這種復雜學習架構的 Rademacher 復雜度的邊界，實際上的方法是在訓練分類器后通過留存集檢測泛化的缺乏。這一領域的每個實踐者都在這樣做（卻沒有意識到），張弛原等人強調了現在的理論毫無助益，這一點值得稱贊。

尋找規范性泛化理論：新論文

在我們的醫學類比中，我們看到醫生至少需要做一次身體檢查才能得到規范性的診斷。這些新論文的作者也直觀地把握住了這一點并且試圖確定可能實現更好泛化的真實神經網絡的性質。幾十年前有人在簡單的 2 層網絡上進行過這樣的分析（與「邊際（margin）」相關），其中的難點是尋找與多層網絡的類比。Bartlett 等人和 Neyshabur 等人都深入研究了深度網絡的層的權重舉證的穩定秩（stable rank）。這些可被看作是「flat minimum」的一個實例，多年來神經網絡方面的文獻一直在討論這個問題。我將在未來的文章中給出我對這些結果的理解和一些改進。注意，這些方法目前還未給出任何有關訓練網絡所需數據點數量的不尋常的邊界。

Dziugaite 和 Roy 選擇了稍有不同的方向。他們的工作始于 McAllester 的 1999 PAC-Bayes 邊界，也即：如果該算法在假設上的先驗分布是 P，那么對于在該假設上的每個后驗分布 Q（可能取決于數據），根據 Q 所選擇的平均分類器的泛化誤差的上界如下，其中 D() 表示 KL 散度：

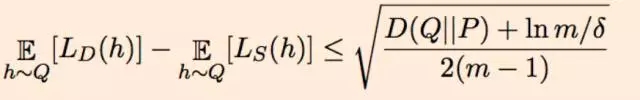
這使得可以通過 Langford 和 Caruana 之前的論文（(Not) Bounding the True Error）中類似的過程為泛化誤差設置上界，其中 P 是均勻高斯，Q 是訓練后的深度網絡的有噪聲版本（我們想要解釋它的泛化）。具體來說，如果 w_ij 是該訓練后網絡中邊 i,j 的權重，那么為權重 w_ij 增加高斯噪聲 η_ij 就構成了 Q。因此根據 Q 所得到的隨機分類器不過是該訓練后網絡的一個有噪聲版本而已。現在我們看到關鍵了：使用非凸優化來尋找 η_ij 的方差的一個選擇，使之能在兩個不相容的指標上找到平衡：（a）源自 Q 的平均分類器的訓練誤差不比原來的訓練后的網絡多很多（同樣，這是通過優化找到的極小值的「平坦度」的量化）；（b）上面表達式的右邊盡可能小。假設（a）和（b）都可以適當地確定邊界，那么源自 Q 的平均分類器可以在未曾見過的數據上表現得相當好。（注意這種方法只是證明了訓練后的分類器的有噪聲版本的泛化能力。）

將這種方法應用到在 MNIST 數據集上訓練的簡單全連接神經網絡上，他們可以證明這種方法可在 MNIST 上實現 17% 的誤差（實際誤差要低得多，在 2% 到 3% 之間）。他們的論文也由此得名，承諾有非空虛（nonvacuous）的泛化邊界。對于這個結果，我覺得最有意思的是它使用了非凸優化的能力（在上面被用來尋找一個合適的噪聲分布 Q）來闡釋有關非凸優化的一個元問題，即深度學習不過擬合的原因是什么。

原文鏈接：http://www.offconvex.org/2017/12/08/generalization1/

商業智能與數據分析群

興趣范圍包括各種讓數據產生價值的辦法，實際應用案例分享與討論，分析工具，ETL工具，數據倉庫，數據挖掘工具，報表系統等全方位知識

QQ群：81035754