摘要：文章第一部分旨在幫助讀者理解卷積的概念和深度學習中的卷積網絡。卷積定理要理解卷積，不得不提，它將時域和空域上的復雜卷積對應到了頻域中的元素間簡單的乘積。

譯者按：本文譯自 Tim Dettmers 的 Understanding Convolution in Deep Learning。有太多的公開課、教程在反復傳頌卷積神經網絡的好，卻都沒有講什么是「卷積」，似乎默認所有讀者都有相關基礎。這篇外文既友好又深入，所以翻譯了過來。文章高級部分通過流體力學量子力學等解釋卷積的做法在我看來有點激進，這些領域恐怕比卷積更深奧，所以只需簡略看看即可。以下是正文：

卷積現在可能是深度學習中最重要的概念。正是靠著卷積和卷積神經網絡，深度學習才超越了幾乎其他所有的機器學習手段。但卷積為什么如此強大？它的原理是什么？在這篇博客中我將講解卷積及相關概念，幫助你徹底地理解它。

網絡上已經有不少博客講解卷積和深度學習中的卷積，但我發現它們都一上來就加入了太多不必要的數學細節，艱深晦澀，不利于理解主旨。這篇博客雖然也有很多數學細節，但我會以可視化的方式一步步展示它們，確保每個人都可以理解。文章第一部分旨在幫助讀者理解卷積的概念和深度學習中的卷積網絡。第二部分引入了一些高級的概念，旨在幫助深度學習方向的研究者和高級玩家進一步加深對卷積的理解。

第一部分：什么是卷積

整篇博客都會探討這個問題，但先把握行文脈絡會很有幫助。那么粗略來講，什么是卷積呢？

你可以把卷積想象成一種混合信息的手段。想象一下裝滿信息的兩個桶，我們把它們倒入一個桶中并且通過某種規則攪拌攪拌。也就是說卷積是一種混合兩種信息的流程。

卷積也可以形式化地描述，事實上，它就是一種數學運算，跟減加乘除沒有本質的區別。雖然這種運算本身很復雜，但它非常有助于簡化更復雜的表達式。在物理和工程上，卷積被廣泛地用于化簡等式——等會兒簡單地形式化描述卷積之后——我們將把這些領域的思想和深度學習聯系起來，以加深對卷積的理解。但現在我們先從實用的角度理解卷積。

我們如何對圖像應用卷積

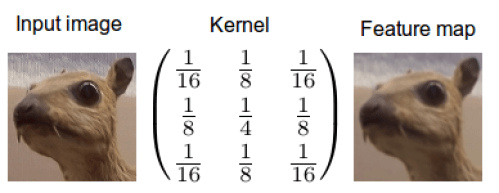
當我們在圖像上應用卷積時，我們在兩個維度上執行卷積——水平和豎直方向。我們混合兩桶信息：第一桶是輸入的圖像，由三個矩陣構成——RGB 三通道，其中每個元素都是 0 到 255 之間的一個整數。第二個桶是卷積核（kernel），單個浮點數矩陣。可以將卷積核的大小和模式想象成一個攪拌圖像的方法。卷積核的輸出是一幅修改后的圖像，在深度學習中經常被稱作 feature map。對每個顏色通道都有一個 feature map。

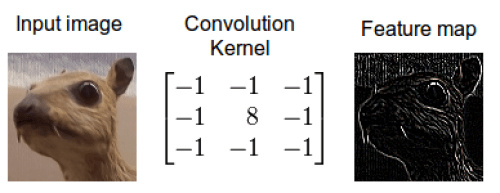
邊緣檢測卷積核的效果

這是怎么做到的呢，我們現在演示一下如何通過卷積來混合這兩種信息。一種方法是從輸入圖片中取出一個與卷積核大小相同的區塊——這里假設圖片為 100×100，卷積核大小為 3×3，那么我們取出的區塊大小就是 3×3——然后對每對相同位置的元素執行乘法后求和（不同于矩陣乘法，卻類似向量內積，這里是兩個相同大小的矩陣的「點乘」）。乘積的和就生成了 feature map 中的一個像素。當一個像素計算完畢后，移動一個像素取下一個區塊執行相同的運算。當無法再移動取得新區塊的時候對 feature map 的計算就結束了。這個流程可以用如下的動畫演示：

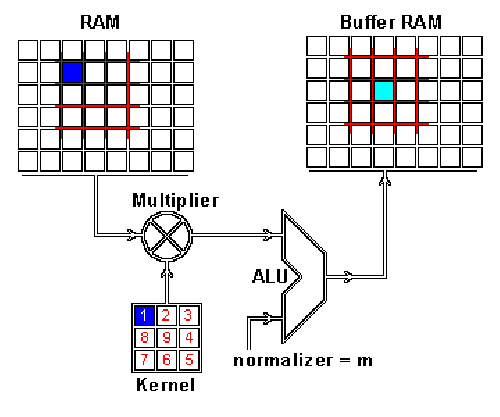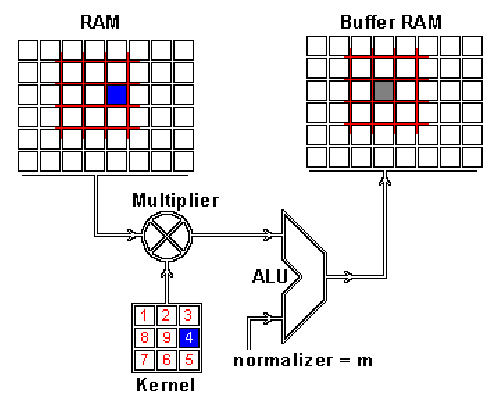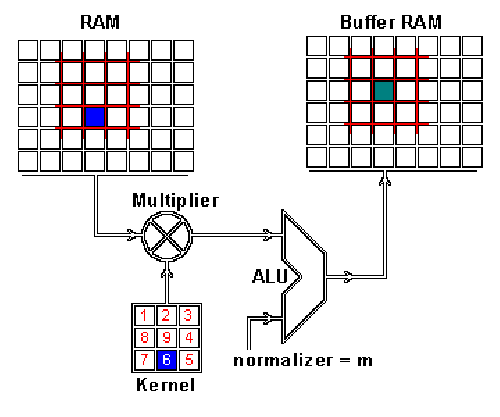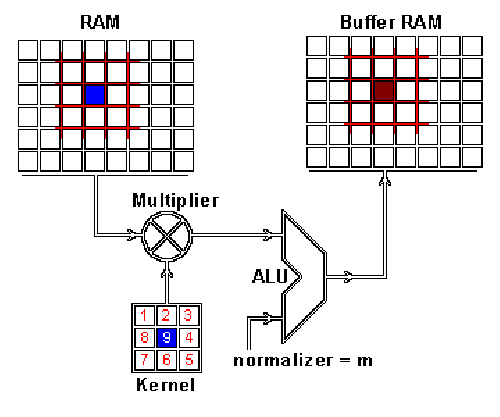
RAM 是輸入圖片，Buffer 是 feature map

你可能注意到這里有個正規化因子 m，這里 m 的值為 kernel 的大小 9；這是為了保證輸入圖像和 feature map 的亮度相同。

為什么機器學習中圖像卷積有用

圖像中可能含有很多我們不關心的噪音。一個好例子是我和 Jannek Thomas 在 Burda Bootcamp 做的項目。Burda Bootcamp 是一個讓學生像黑客馬拉松一樣在非常短的時間內創造技術風暴的實驗室。與 9 名同事一起，我們在 2 個月內做了 11 個產品出來。其中之一是針對時尚圖像用深度編碼器做的搜索引擎：你上傳一幅時尚服飾的圖片，編碼器自動找出款式類似的服飾。

如果你想要區分衣服的式樣，那么衣服的顏色就不那么重要了；另外像商標之類的細節也不那么重要。最重要的可能是衣服的外形。一般來講，女裝襯衫的形狀與襯衣、夾克和褲子的外觀非常不同。如果我們過濾掉這些多余的噪音，那我們的算法就不會因顏色、商標之類的細節分心了。我們可以通過卷積輕松地實現這項處理。

我的同事 Jannek Thomas 通過索貝爾邊緣檢測濾波器（與上上一幅圖類似）去掉了圖像中除了邊緣之外的所有信息——這也是為什么卷積應用經常被稱作濾波而卷積核經常被稱作濾波器（更準確的定義在下面）的原因。由邊緣檢測濾波器生成的 feature map 對區分衣服類型非常有用，因為只有外形信息被保留下來。

彩圖的左上角是搜索 query，其他是搜索結果，你會發現自動編碼器真的只關注衣服的外形，而不是顏色。

再進一步：有許多不同的核可以產生多種 feature map，比如銳化圖像（強調細節），或者模糊圖像（減少細節），并且每個 feature map 都可能幫助算法做出決策（一些細節，比如衣服上有 3 個紐扣而不是兩個，可能可以區分一些服飾）。

使用這種手段——讀入輸入、變換輸入、然后把 feature map 喂給某個算法——被稱為特征工程。特征工程非常難，很少有資料幫你上手。造成的結果是，很少有人能熟練地在多個領域應用特征工程。特征工程是——純手工——也是 Kaggle 比賽中最重要的技能。特征工程這么難的原因是，對每種數據每種問題，有用的特征都是不同的：圖像類任務的特征可能對時序類任務不起作用；即使兩個任務都是圖像類的，也很難找出相同的有效特征，因為視待識別的物體的不同，有用的特征也不同。這非常依賴經驗。

所以特征工程對新手來講特別困難。不過對圖像而言，是否可以利用卷積核自動找出某個任務中最適合的特征？

進入卷積神經網絡

卷積神經網絡就是干這個的。不同于剛才使用固定數字的卷積核，我們賦予參數給這些核，參數將在數據上得到訓練。隨著卷積神經網絡的訓練，這些卷積核為了得到有用信息，在圖像或 feature map 上的過濾工作會變得越來越好。這個過程是自動的，稱作特征學習。特征學習自動適配新的任務：我們只需在新數據上訓練一下自動找出新的過濾器就行了。這是卷積神經網絡如此強大的原因——不需要繁重的特征工程了！

通常卷積神經網絡并不學習單一的核，而是同時學習多層級的多個核。比如一個 32x16x16 的核用到 256×256 的圖像上去會產生 32 個 241×241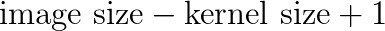（）的 feature map。所以自動地得到了 32 個有用的新特征。這些特征可以作為下個核的輸入。一旦學習到了多級特征，我們簡單地將它們傳給一個全連接的簡單的神經網絡，由它完成分類。這就是在概念上理解卷積神經網絡所需的全部知識了（池化也是個重要的主題，但還是在另一篇博客中講吧）。

第二部分：高級概念

我們現在對卷積有了一個良好的初步認識，也知道了卷積神經網絡在干什么、為什么它如此強大。現在讓我們深入了解一下卷積運算中到底發生了什么。我們將認識到剛才對卷積的講解是粗淺的，并且這里有更優雅的解釋。通過深入理解，我們可以理解卷積的本質并將其應用到許多不同的數據上去。萬事開頭難，第一步是理解卷積原理。

卷積定理

要理解卷積，不得不提 convolution theorem，它將時域和空域上的復雜卷積對應到了頻域中的元素間簡單的乘積。這個定理非常強大，在許多科學領域中得到了廣泛應用。卷積定理也是快速傅里葉變換算法被稱為 20 世紀最重要的算法之一的一個原因。

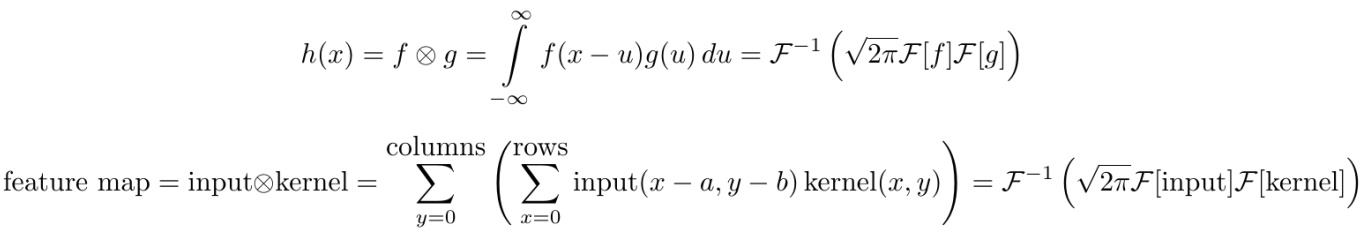
第一個等式是一維連續域上兩個連續函數的卷積；第二個等式是二維離散域（圖像）上的卷積。這里指的是卷積，指的是傅里葉變換，表示傅里葉逆變換，是一個正規化常量。這里的「離散」指的是數據由有限個變量構成（像素）；一維指的是數據是一維的（時間），圖像則是二維的，視頻則是三維的。

為了更好地理解卷積定理，我們還需要理解數字圖像處理中的傅里葉變換。

快速傅里葉變換

快速傅里葉變換是一種將時域和空域中的數據轉換到頻域上去的算法。傅里葉變換用一些正弦和余弦波的和來表示原函數。必須注意的是，傅里葉變換一般涉及到復數，也就是說一個實數被變換為一個具有實部和虛部的復數。通常虛部只在一部分領域有用，比如將頻域變換回到時域和空域上；而在這篇博客里會被忽略掉。你可以在下面看到一個信號（一個以時間為參數的有周期的函數通常稱為信號）是如何被傅里葉變換的：

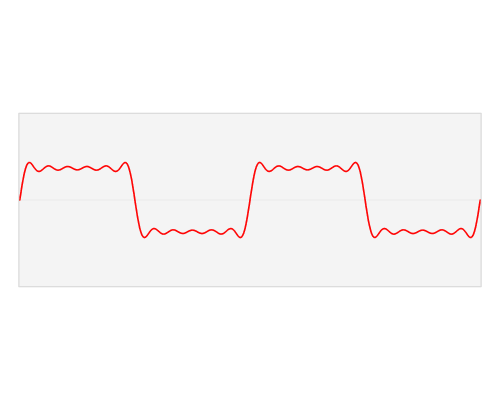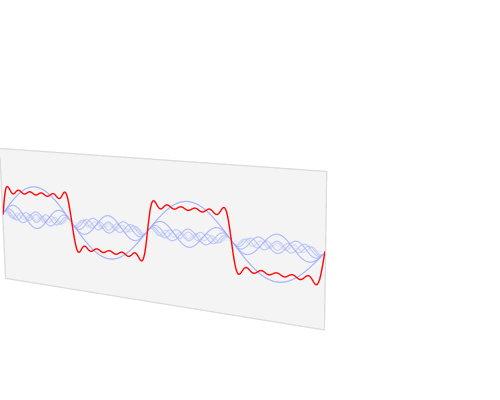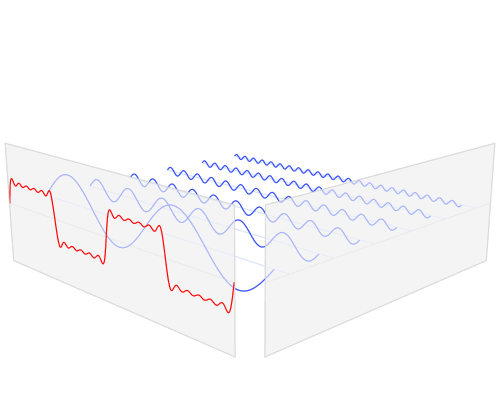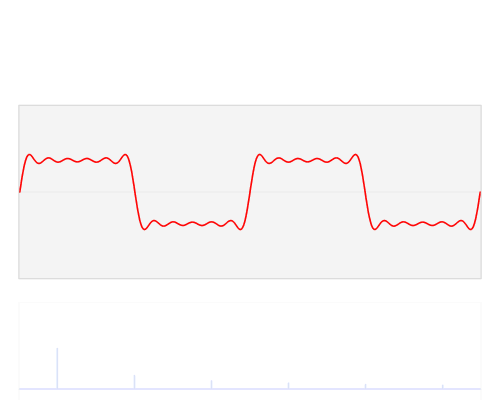
紅色是時域，藍色為頻域

你也許會說從沒見過這些東西，但我敢肯定你在生活中是見過的：如果紅色是一首音樂的話，那么藍色值就是你在你的 MP3 播放器屏幕上看到的頻譜：

傅里葉域上的圖像

我們如何想象圖片的頻率呢？想象一張只有兩種模式的紙片，現在把紙片豎起來順著線條的方向看過去，就會看到一個一個的亮點。這些以一定間隔分割黑白部分的波就代表著頻率。在頻域中，低頻率更接近中央而高頻率更接近邊緣。頻域中高強度（亮度、白色）的位置代表著原始圖像亮度改變的方向。這一點在接下來這張圖與其對數傅里葉變換（對傅里葉變換的實部取對數，這樣可以減小像素亮度的差別，便于觀察更廣的亮度區域）中特別明顯：

我們馬上就可以發現傅里葉變換包含了關于物體朝向的信息。如果物體被旋轉了一個角度，從圖像像素上可能很難判斷，但從頻域上可以很明顯地看出來。

這是個很重要的啟發，基于傅里葉定理，我們知道卷積神經網絡在頻域上檢測圖像并且捕捉到了物體的方向信息。于是卷積神經網絡就比傳統算法更擅長處理旋轉后的圖像（雖然還是比不上人類）。

頻率過濾與卷積

為什么卷積經常被描述為過濾，為什么卷積核經常被稱為過濾器呢？通過下一個例子可以解釋：

如果我們對圖像執行傅里葉變換，并且乘以一個圓形（背景填充黑色，也就是 0），我們可以過濾掉所有的高頻值（它們會成為 0，因為填充是 0）。注意過濾后的圖像依然有條紋模式，但圖像質量下降了很多——這就是 jpeg 壓縮算法的工作原理（雖然有些不同但用了類似的變換），我們變換圖形，然后只保留部分頻率，最后將其逆變換為二維圖片；壓縮率就是黑色背景與圓圈的比率。

我們現在將圓圈想象為一個卷積核，然后就有了完整的卷積過程——就像在卷積神經網絡中看到的那樣。要穩定快速地執行傅里葉變換還需要許多技巧，但這就是基本理念了。

現在我們已經理解了卷積定理和傅里葉變換，我們可以將這些理念應用到其他科學領域，以加強我們對深度學習中的卷積的理解。

流體力學的啟發

流體力學為空氣和水創建了大量的微分方程模型，傅里葉變換不但簡化了卷積，也簡化了微分，或者說任何利用了微分方程的領域。有時候得到解析解的方法就是對微分方程左右同時執行傅里葉變換。在這個過程中，我們常常將解寫成兩個函數卷積的形式，以得到更簡單的表達。這是在一個維度上的應用，還有在兩個維度上的應用，比如天文學。

擴散

你可以混合兩種液體（牛奶和咖啡），只要施加一個外力（湯勺攪拌）——這被稱為對流，而且是個很快的過程。你也可以耐心等待兩種液體自然混合——這被稱為擴散，通常是很慢的過程。

想象一下，一個魚缸被一塊板子隔開，兩邊各有不同濃度的鹽水。抽掉板子后，兩邊的鹽水會逐步混合為同一個濃度。濃度差越大，這個過程越劇烈。

現在想象一下，一個魚缸被 256×256 個板子分割為 256×256 個部分（這個數字似乎不對），每個部分都有不同濃度的鹽水。如果你去掉所有的擋板，濃度類似的小塊間將不會有多少擴散，但濃度差異大的區塊間有巨大的擴散。這些小塊就是像素點，而濃度就是像素的亮度。濃度的擴散就是像素亮度的擴散。

這說明，擴散現象與卷積有相似點——初始狀態下不同濃度的液體，或不同強度的像素。為了完成下一步的解釋，我們還需要理解傳播子。

理解傳播子

傳播子就是密度函數，表示流體微粒應該往哪個方向傳播。問題是神經網絡中沒有這樣的概率函數，只有一個卷積核——我們要如何統一這兩種概念呢？

我們可以通過正規化來講卷積核轉化為概率密度函數。這有點像計算輸出值的 softmax。下面就是對第一個例子中的卷積核執行的 softmax 結果：

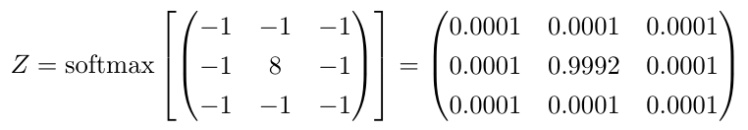
現在我們就可以從擴散的角度來理解圖像上的卷積了。我們可以把卷積理解為兩個擴散流程。首先，當像素亮度改變時（黑色到白色等）會發生擴散；然后某個區域的擴散滿足卷積核對應的概率分布。這意味著卷積核正在處理的區域中的像素點必須按照這些概率來擴散。

在上面那個邊緣檢測器中，幾乎所有臨近邊緣的信息都會聚集到邊緣上（這在流體擴散中是不可能的，但這里的解釋在數學上是成立的）。比如說所有低于 0.0001 的像素都非常可能流動到中間并累加起來。與周圍像素區別較大的區域會成為強度的集中地，因為擴散最劇烈。反過來說，強度最集中的地方說明與周圍對比最強烈，這也就是物體的邊緣所在，這解釋了為什么這個核是一個邊緣檢測器。

所以我們就得到了物理解釋：卷積是信息的擴散。我們可以直接把這種解釋運用到其他核上去，有時候我們需要先執行一個 softmax 正規化才能解釋，但一般來講核中的數字已經足夠說明它想要干什么。比如說，你是否能推斷下面這個核的的意圖？

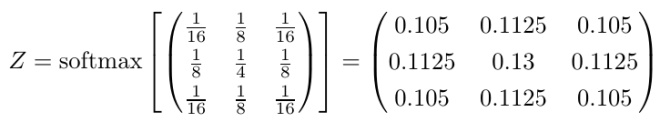
等等，有點迷惑

對一個概率化的卷積核，怎么會有確定的功能？我們必須根據核對應的概率分布也就是傳播子來計算單個粒子的擴散不是嗎？

是的，確實如此。但是，如果你取一小部分液體，比如一滴水，你仍然有幾百萬水分子。雖然單個分子的隨機移動滿足傳播子，但大量的分子宏觀上的表現是基本確定的。這是統計學上的解釋，也是流體力學的解釋。我們可以把傳播子的概率分布解釋為信息或說像素亮度的平均分布；也就是說我們的解釋從流體力學的角度來講是沒問題的。話說回來，這里還有一個卷積的隨機解釋。

量子力學的啟發

傳播子是量子力學中的重要概念。在量子力學中，一個微粒可能處于一種疊加態，此時它有兩個或兩個以上屬性使其無法確定位于觀測世界中的具體位置。比如，一個微粒可能同時存在于兩個不同的位置。

但是如果你測量微粒的狀態——比如說現在微粒在哪里——它就只能存在于一個具體位置了。換句話說，你通過觀測破壞了微粒的疊加態。傳播子就描述了微粒出現位置的概率分布。比如說在測量后一個微粒可能——根據傳播子的概率函數——30% 在 A，70% 在 B。

通過量子糾纏，幾個粒子就可以同時儲存上百或上百萬個狀態——這就是量子計算機的威力。

如果我們將這種解釋用于深度學習，我們可以把圖片想象為位于疊加態，于是在每個 3*3 的區塊中，每個像素同時出現在 9 個位置。一旦我們應用了卷積，我們就執行了一次觀測，然后每個像素就坍縮到滿足概率分布的單個位置上了，并且得到的單個像素是所有像素的平均值。為了使這種解釋成立，必須保證卷積是隨機過程。這意味著，同一個圖片同一個卷積核會產生不同的結果。這種解釋沒有顯式地把誰比作誰，但可能啟發你如何把卷積用成隨機過程，或如何發明量子計算機上的卷積網絡算法。量子算法能夠在線性時間內計算出卷積核描述的所有可能的狀態組合。

概率論的啟發

卷積與互相關緊密相連。互相關是一種衡量小段信息（幾秒鐘的音樂片段）與大段信息（整首音樂）之間相似度的一種手段（youtube 使用了類似的技術檢測侵權視頻）。

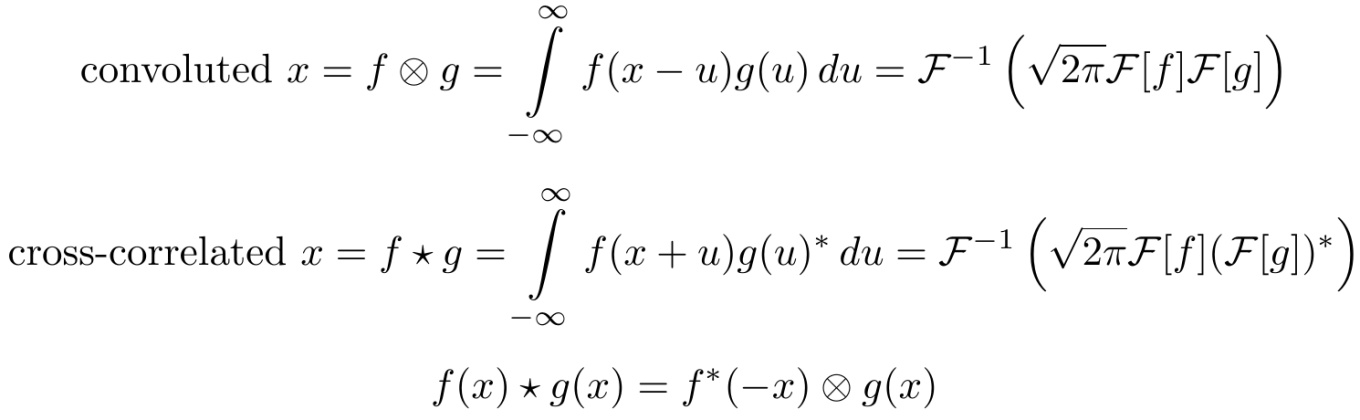
雖然互相關的公式看起來很難，但通過如下手段我們可以馬上看到它與深度學習的聯系。在圖片搜索中，我們簡單地將 query 圖片上下顛倒作為核然后通過卷積進行互相關檢驗，結果會得到一張有一個或多個亮點的圖片，亮點所在的位置就是人臉所在的位置。

這個例子也展示了通過補零來使傅里葉變換穩定的一種技巧，許多版本的傅里葉變換都使用了這種技巧。另外還有使用了其他 padding 技巧：比如平鋪核，分治等等。我不會展開講，關于傅里葉變換的文獻太多了，里面的技巧特別多——特別是對圖像來講。

在更底層，卷積網絡第一層不會執行互相關校驗，因為第一層執行的是邊緣檢測。后面的層得到的都是更抽象的特征，就有可能執行互相關了。可以想象這些亮點像素會傳遞給檢測人臉的單元（Google Brain 項目的網絡結構中有一些單元專門識別人臉、貓等等；也許用的是互相關？）

統計學的啟發

統計模型和機器學習模型的區別是什么？統計模型只關心很少的、可以解釋的變量。它們的目的經常是回答問題：藥品 A 比藥品 B 好嗎？

機器學習模型是專注于預測效果的：對于年齡 X 的人群，藥品 A 比 B 的治愈率高 17%，對年齡 Y 則是 23%。

機器學習模型通常比統計模型更擅長預測，但它們不是那么可信。統計模型更擅長得到準確可信的結果：就算藥品 A 比 B 好 17%，我們也不知道這是不是偶然，我們需要統計模型來判斷。

對時序數據，有兩種重要的模型：weighted moving average 和 autoregressive 模型，后者可歸入 ARIMA model (autoregressive integrated moving average model)。比起 LSTM，ARIMA 很弱。但在低維度數據（1-5 維）上，ARIMA 非常健壯。雖然它們有點難以解釋，但 ARIMA 絕不是像深度學習算法那樣的黑盒子。如果你需要一個可信的模型，這是個巨大的優勢。

我們可以將這些統計模型寫成卷積的形式，然后深度學習中的卷積就可以解釋為產生局部 ARIMA 特征的函數了。這兩種形式并不完全重合，使用需謹慎。

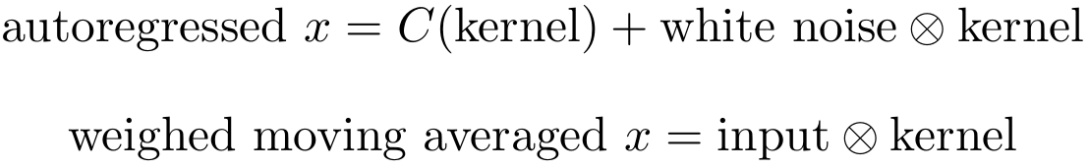
C 是一個以核為參數的函數，white noise 是正規化的均值為 0 方差為 1 的互不相關的數據。

當我們預處理數據的時候，經常將數據處理為類似 white noise 的形式：將數據移動到均值為 0，將方差調整為 1。我們很少去除數據的相關性，因為計算復雜度高。但是在概念上是很簡單的，我們旋轉坐標軸以重合數據的特征向量：

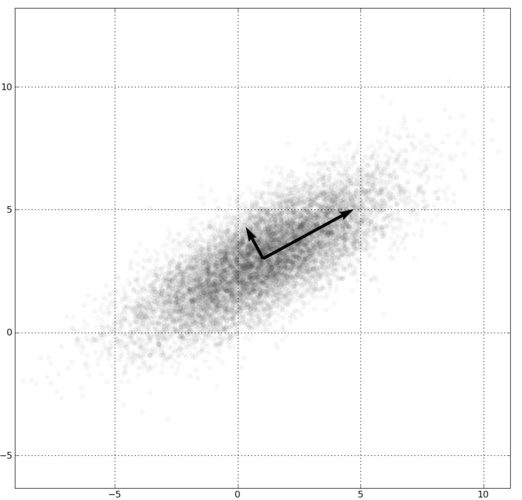
現在如果我們將 C 作為 bias，我們就會覺得這與卷積神經網絡很像。所以卷積層的輸出可被解釋為白噪音數據經過 autoregressive model 的輸出。

weighted moving average 的解釋更簡單：就是輸入數據與某個固定的核的卷積。看看文末的高斯平滑核就會明白這個解釋。高斯平滑核可以被看做每個像素與其鄰居的平均，或者說每個像素被其鄰居平均（邊緣模糊）。

雖然單個核無法同時創建 autoregressive 和 weighted moving average 特征，但我們可以使用多個核來產生不同的特征。

總結

這篇博客中我們知道了卷積是什么、為什么在深度學習中這么有用。圖片區塊的解釋很容易理解和計算，但有其理論局限性。我們通過學習傅里葉變換知道傅里葉變換后的時域上有很多關于物體朝向的信息。通過強大的卷積定理我們理解了卷積是一種在像素間的信息流動。之后我們拓展了量子力學中傳播子的概念，得到了一個確定過程中的隨機解釋。我們展示了互相關與卷積的相似性，并且卷積網絡的性能可能是基于 feature map 間的互相關程度的，互相關程度是通過卷積校驗的。最后我們將卷積與兩種統計模型關聯了起來。

個人來講，我覺得寫這篇博客很有趣。曾經很長一段時間我都覺得本科的數學和統計課是浪費時間，因為它們太不實用了（哪怕是應用數學）。但之后——就像突然中大獎一樣——這些知識都相互串起來了并且帶了新的理解。我覺得這是個絕妙的例子，啟示我們應該耐心地學習所有的大學課程——哪怕它們一開始看起來沒有用。

上文高斯平滑核問題的答案

Reference

http://timdettmers.com/2015/03/26/convolution-deep-learning/?

R. B. Fisher, K. Koryllos,「Interactive Textbooks; Embedding Image Processing Operator Demonstrations in Text」, Int. J. of Pattern Recognition and Artificial Intelligence, Vol 12, No 8, pp 1095-1123, 1998.

原英文鏈接：http://timdettmers.com/2015/03/26/convolution-deep-learning/

商業智能與數據分析群

興趣范圍包括各種讓數據產生價值的辦法，實際應用案例分享與討論，分析工具，ETL工具，數據倉庫，數據挖掘工具，報表系統等全方位知識

QQ群：81035754