摘要：實際的反卷積會使卷積過程恢復。轉置卷積層執行常規卷積，但恢復其空間變換。轉換卷積，沒有填充，步幅為，內核為轉置卷積不會這樣做。在神經網絡中，我們通常使用稱為深度可分離卷積的東西。

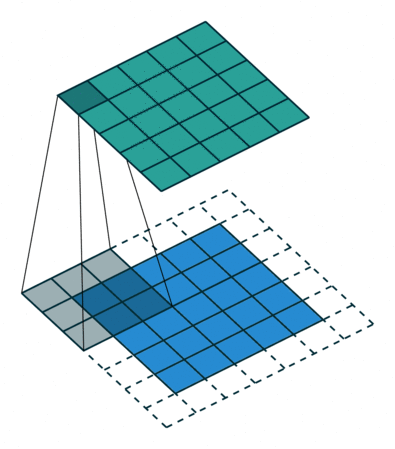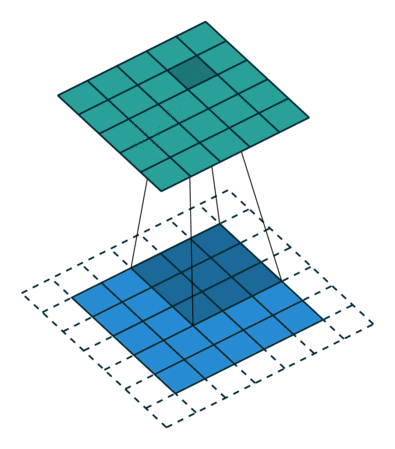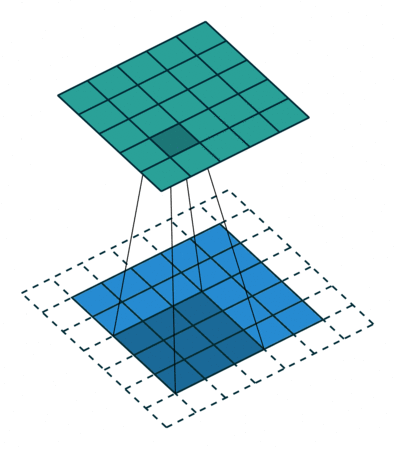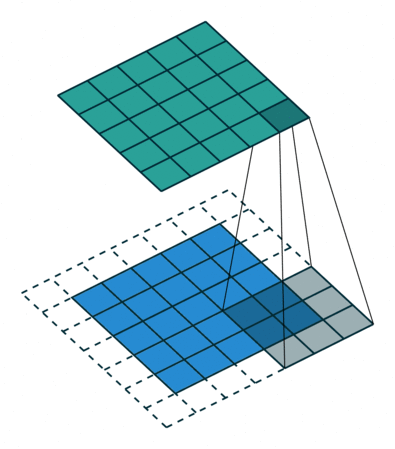
使用內核大小為3，步長為1和填充的2D卷積

一般卷積

首先，我們需要就定義卷積層的一些參數達成一致。

卷積核大小（Kernel Size）：卷積核定義了卷積的大小范圍，二維卷積核最常見的就是 3*3 的卷積核。

步長（Stride）：步長定義了當卷積核在圖像上面進行卷積操作的時候，每次卷積跨越的長度。在默認情況下，步長通常為 1，但我們也可以采用步長是 2 的下采樣過程，類似于 MaxPooling 操作。

填充（Padding）：卷積層采用一定數量的輸入通道（I），并且設計特定數量的輸出通道（O）。每一層所需的參數可以通過 I*O*K 來進行計算，其中 K 等于卷積核的數量。

輸入和輸出管道（Input & Output Channels）：卷積層采用一定數量的輸入通道

擴張的卷積

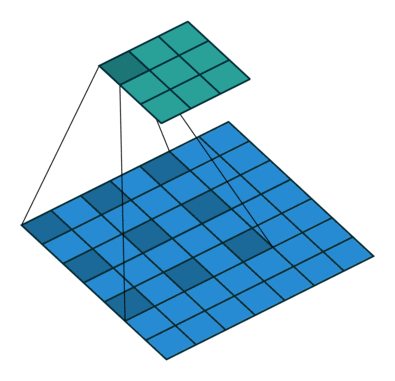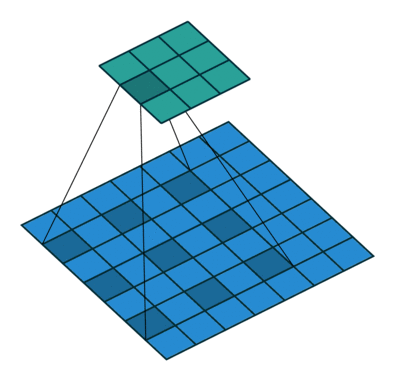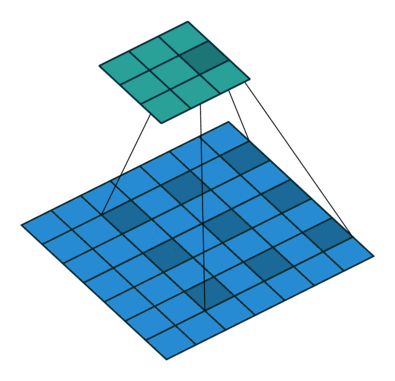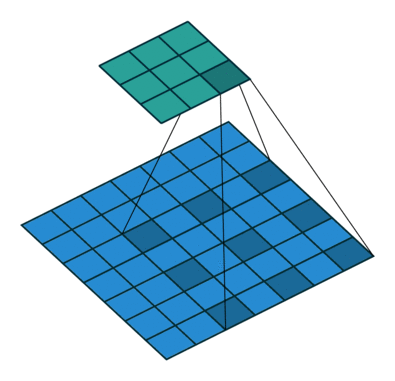
使用3內核進行2D卷積，擴展率為2且無填充

擴張的卷積為卷積層引入另一個參數，稱為擴張率。這定義了卷積核中值之間的間距。擴張率為2的3x3內核與5x5內核具有相同的視野，而僅使用9個參數。想象一下，獲取一個5x5內核并刪除每一個第二列和第二行（間隔刪除），就是我們介紹的卷積。

這以相同的計算成本提供了更寬的視野。擴張卷積在實時分割領域中特別受歡迎。如果您需要廣泛的視野并且無法承受多個卷積或更大的核，請使用它們。

轉置卷積

（又稱解卷積或分數跨度卷積）

有些消息來源使用名稱deconvolution，這是不合適的，因為它不是解卷積。為了使事情更糟，確實存在解卷積，但它們在深度學習領域并不常見。實際的反卷積會使卷積過程恢復。想象一下，將圖像輸入到單個卷積層中。現在取出輸出，將它扔進一個黑盒子里然后再出現原始圖像。這個黑盒子進行反卷積。它是卷積層的數學逆。

轉置卷積有點類似，因為它產生與假設的反卷積層相同的空間分辨率。但是，對值執行的實際數學運算是不同的。轉置卷積層執行常規卷積，但恢復其空間變換。

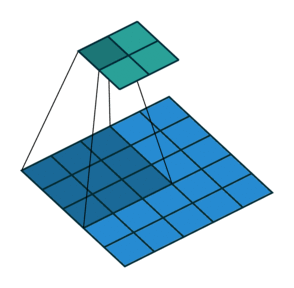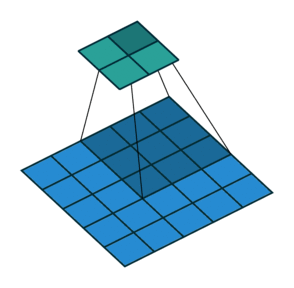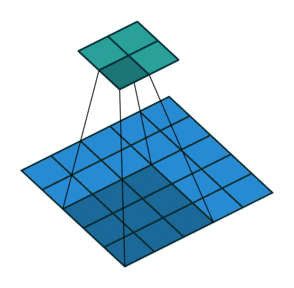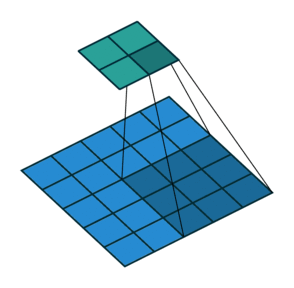
2D卷積，沒有填充，步幅為2，內核為3

此時你應該很困惑，讓我們看一個具體的例子。將5×5的圖像送入卷積層。步幅設置為2，填充停用，內核為3x3。這導致2x2圖像。

如果我們想要反轉這個過程，我們需要逆數學運算，以便從我們輸入的每個像素生成9個值。然后，我們以2的步幅遍歷輸出圖像。這將是反卷積。

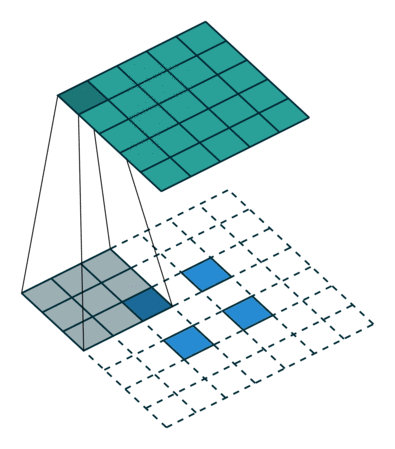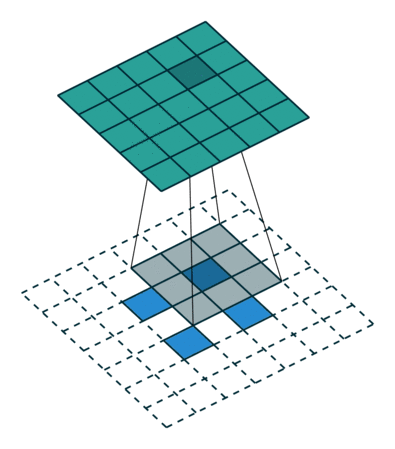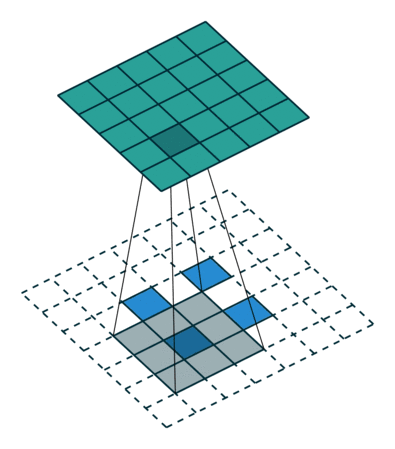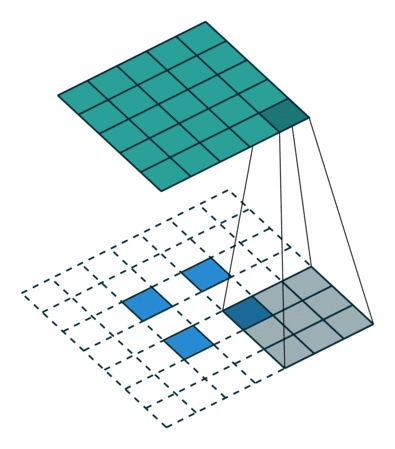
轉換2D卷積，沒有填充，步幅為2，內核為3

轉置卷積不會這樣做。的共同點是它保證輸出也是5x5圖像，同時仍然執行正常的卷積操作。為此，我們需要在輸入上執行一些花哨的填充。

正如您現在可以想象的那樣，此步驟不會從上面顛倒過程。至少不涉及數值。

它只是從之前重建空間分辨率并執行卷積。這可能不是數學逆，但對于編碼器 - 解碼器架構，它仍然非常有用。這樣我們就可以將圖像的升級與卷積相結合，而不是進行兩個多帶帶的處理。

可分離的卷積

在可分離的卷積中，我們可以將內核操作分成多個步驟。讓我們將卷積表示為y = conv（x，k），其中y是輸出圖像，x是輸入圖像，k是核。簡單。接下來，假設k可以通過以下公式計算：k = k1.dot（k2）。這將使它成為可分離的卷積，因為我們可以通過用k1和k2進行2個1D卷積來得到相同的結果，而不是用k進行2D卷積。

Sobel X和Y濾鏡

以Sobel內核為例，它通常用于圖像處理。你可以通過乘以向量[1,0，-1]和[1,2,1] .T得到相同的內核。在執行相同操作時，這將需要6個而不是9個參數。上面的例子顯示了所謂的空間可分卷積，據我所知，它不用于深度學習。

編輯：實際上，通過堆疊1xN和Nx1內核層，可以創建與空間可分離卷積非常相似的東西。這最近在一個名為EffNet的架構中使用，顯示了有希望的結果。

在神經網絡中，我們通常使用稱為深度可分離卷積的東西。這將執行空間卷積，同時保持通道分離，然后進行深度卷積。在我看來，通過一個例子可以較好地理解它。

假設我們在16個輸入通道和32個輸出通道上有一個3x3卷積層。詳細情況是，32個3x3核遍歷16個通道中的每個通道，產生512（16x32）個特征映射。接下來，我們通過添加它們來合并每個輸入通道中的1個特征圖。由于我們可以做32次，我們得到了我們想要的32個輸出通道。

對于同一示例中的深度可分離卷積，我們遍歷16個通道，每個通道有1個3x3內核，為我們提供了16個特征映射。現在，在合并任何東西之前，我們遍歷這16個特征映射，每個特征映射有32個1x1卷積，然后才開始將它們加在一起。這導致656（16x3x3 + 16x32x1x1）參數與上面的4608（16x32x3x3）參數相反。

該示例是深度可分離卷積的特定實現，其中所謂的深度乘數為1.這是迄今為止這種層的最常見設置。我們這樣做是因為空間和深度信息可以解耦的假設。看一下Xception模型的表現，這個理論似乎有效。由于其有效使用參數，深度可分離卷積也用于移動設備。

商業智能與數據分析群

興趣范圍包括各種讓數據產生價值的辦法，實際應用案例分享與討論，分析工具，ETL工具，數據倉庫，數據挖掘工具，報表系統等全方位知識

QQ群：81035754