資訊專欄INFORMATION COLUMN

摘要:我們將這些現(xiàn)象籠統(tǒng)稱為廣義的模式崩潰問(wèn)題。這給出了模式崩潰的直接解釋。而傳統(tǒng)深度神經(jīng)網(wǎng)絡(luò)只能逼近連續(xù)映射,這一矛盾造成了模式崩潰。
春節(jié)前夕,北美遭遇極端天氣,在酷寒中筆者來(lái)到哈佛大學(xué)探望丘成桐先生。新春佳節(jié),本是普天同慶的日子,但對(duì)于孤懸海外的游子而言,卻是更為凄涼難耐。遠(yuǎn)離父母親朋,遠(yuǎn)離故國(guó)家園,自然環(huán)境寒風(fēng)凜冽,飛雪漫天,社會(huì)環(huán)境疏離淡漠,冷清寂寥。在波士頓見(jiàn)到導(dǎo)師和朋友,倍感欣慰。筆者曾經(jīng)輔導(dǎo)過(guò)的Kylie剛剛從哈佛畢業(yè)。哈佛本科生的主流一般選擇進(jìn)入華爾街的金融公司,Kylie卻特立獨(dú)行地選擇了教育。筆者輔導(dǎo)過(guò)的Simon剛剛被哈佛錄取,矢志投身數(shù)學(xué)。在查爾斯河畔的LegalSeafood, Kylie給了Simon很多在哈佛求學(xué)的建議。看到弟子們的茁壯成長(zhǎng),筆者不禁感慨萬(wàn)千:時(shí)光荏苒,昭華流逝,人生苦短,擇英才而教之,生命才會(huì)更有意義!
筆者和哈佛大學(xué)統(tǒng)計(jì)系的劉軍教授交流,劉教授告訴筆者最近有麻省理工的學(xué)者來(lái)哈佛尋求教職,求職學(xué)術(shù)演講的主題就是最優(yōu)傳輸理論在深度學(xué)習(xí)中的應(yīng)用。由此可以,深度學(xué)習(xí)的最優(yōu)傳輸理論解釋逐漸被廣泛接受。在哈佛大學(xué)的數(shù)學(xué)科學(xué)與應(yīng)用中心(Harvard CMSA),丘先生和筆者進(jìn)一步探討深度學(xué)習(xí)中對(duì)抗生成網(wǎng)絡(luò)和蒙日-安培方程理論的關(guān)系。
遙想二十多年前,筆者剛剛投到丘先生門下的時(shí)候,丘先生教給筆者的第一個(gè)幾何分析的利器就是蒙日-安培方程理論(Monge-Ampere Equation)。那時(shí),筆者在麻省理工大學(xué)學(xué)習(xí)機(jī)器視覺(jué)課程,需要求解閔科夫斯基(Minkowski)問(wèn)題,即利用高斯曲率反求曲面形狀。丘先生指導(dǎo)筆者用蒙日-安培方程來(lái)解決這一問(wèn)題。當(dāng)時(shí)無(wú)論如何也無(wú)法想象二十多年后,這一理論會(huì)在深度學(xué)習(xí)領(lǐng)域發(fā)揮重要作用。
近些年來(lái),深度學(xué)習(xí)的革命幾乎席卷了整個(gè)計(jì)算機(jī)科學(xué)領(lǐng)域,尤其是這兩年來(lái)對(duì)抗生成網(wǎng)絡(luò)模型(GAN)石破天驚、一騎絕塵,而蒙日-安培理論恰好可以為GAN提供強(qiáng)有力的理論支持。多少年來(lái),丘先生一直強(qiáng)調(diào)基礎(chǔ)理論的重要性,他曾經(jīng)多次說(shuō)道:“人類歷史上技術(shù)的本質(zhì)發(fā)展都是來(lái)自基礎(chǔ)理論的重大突破,基礎(chǔ)理論突破后往往經(jīng)過(guò)數(shù)十年才會(huì)被工程技術(shù)領(lǐng)域所領(lǐng)會(huì)吸收。因此,對(duì)于科學(xué)的發(fā)展應(yīng)該持有長(zhǎng)遠(yuǎn)的觀點(diǎn),不能急功近利。”在筆者數(shù)十年的學(xué)術(shù)生涯中,多次見(jiàn)證了丘先生所預(yù)言的情形發(fā)生,例如陳類之于拓?fù)浣^緣體,證明龐加萊猜測(cè)的黎奇曲率流(Ricci FLow)之于醫(yī)學(xué)圖像。
目前,筆者和很多合作者們傾向于認(rèn)為蒙日-安培理論,最優(yōu)傳輸理論對(duì)深度學(xué)習(xí)的發(fā)展會(huì)起到實(shí)質(zhì)性作用,并為之孜孜以求。這次和丘先生主要討論蒙日-安培方程正則性理論關(guān)于GAN模型中模式崩潰(Mode Collapse)的解釋,細(xì)節(jié)請(qǐng)見(jiàn)論文【1】。
模式崩潰 (Mode Collapse)
對(duì)抗生成網(wǎng)絡(luò)被廣泛應(yīng)用于圖像生成領(lǐng)域,比較常用的有超分辨率、圖像翻譯、卡通人物生成、人體姿態(tài)生成、年齡變換、風(fēng)格變換等等,超乎想象,精彩紛呈。另一方面,GAN模型訓(xùn)練困難,變化無(wú)常,神秘莫測(cè)。由于其強(qiáng)烈的不穩(wěn)定性,目前難以大規(guī)模實(shí)用。
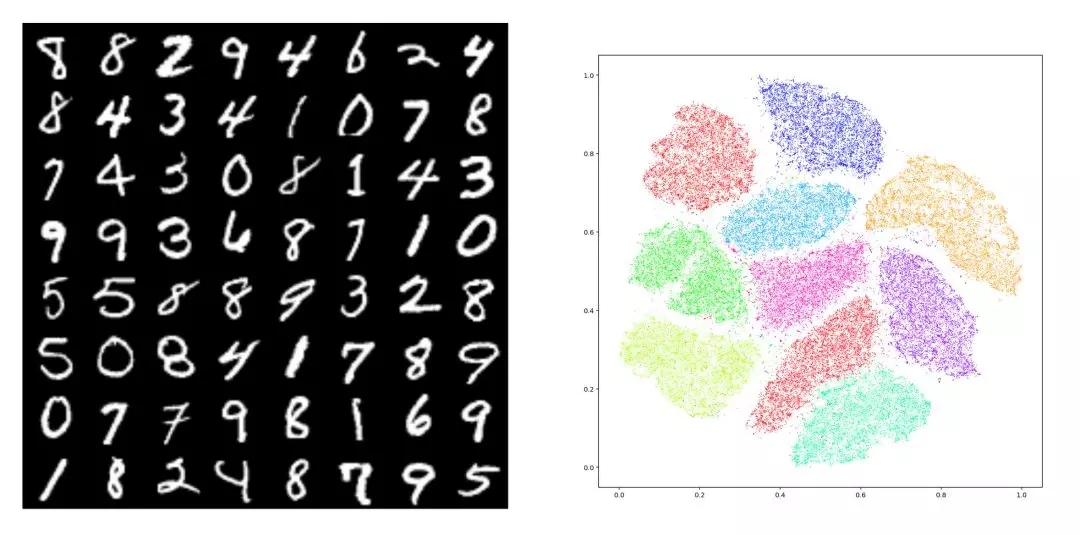
圖1. MNIST數(shù)據(jù)集 tSNE 嵌入在平面上,10個(gè)團(tuán)簇對(duì)應(yīng)著10個(gè)模式(modes)。模式崩潰(Mode Collapse)指生成模型只生成其中的幾種模式。
如圖1所示,給定數(shù)據(jù)集合,我們用編碼映射將其映入隱空間中,每個(gè)數(shù)字對(duì)應(yīng)一個(gè)團(tuán)簇,即MNIST數(shù)據(jù)的概率分布密度函數(shù)具有多個(gè)峰值,每個(gè)峰值被稱為是一個(gè)模式(mode)。理想情況下,生成模型應(yīng)該能夠生成10個(gè)數(shù)字,如果只能生成其中的幾個(gè),而錯(cuò)失其它的模式,則我們稱這種現(xiàn)象為模式崩潰(mode collapse)。
具體而言,GAN訓(xùn)練中經(jīng)常出現(xiàn)如下三個(gè)層次的問(wèn)題:
訓(xùn)練過(guò)程難以收斂,經(jīng)常出現(xiàn)震蕩;實(shí)驗(yàn)結(jié)果隨機(jī),難以復(fù)現(xiàn);
訓(xùn)練收斂,但是出現(xiàn)模式崩潰(Mode Collapse)。例如,我們用MNIST數(shù)據(jù)集訓(xùn)練GAN模型,訓(xùn)練后的GAN只能生成十個(gè)數(shù)字中的某一個(gè);或者在人臉圖片的實(shí)驗(yàn)中,只生成某一種風(fēng)格的圖片。
用真實(shí)圖片訓(xùn)練后的GAN模型涵蓋所有模式,但是同時(shí)生成一些沒(méi)有意義、或者現(xiàn)實(shí)中不可能出現(xiàn)的圖片。
我們將這些現(xiàn)象籠統(tǒng)稱為廣義的模式崩潰問(wèn)題。如何解釋模式崩潰的原因,如何設(shè)計(jì)新型算法避免模式崩潰,這些是深度學(xué)習(xí)領(lǐng)域的更為基本的問(wèn)題。我們用最優(yōu)傳輸中的Brenier理論,和蒙日-安培方程(Monge-Ampere)的正則性(regularity)理論來(lái)解釋模式崩潰問(wèn)題。
GAN和蒙日-安培方程
我們以前討論過(guò)對(duì)抗生成網(wǎng)絡(luò)的最優(yōu)傳輸觀點(diǎn):生成器(Generator)將隱空間的高斯分布變換成數(shù)據(jù)流形上一個(gè)分布,判別器(Discriminator)計(jì)算生成分布和真實(shí)數(shù)據(jù)分布之間的距離,例如Wasserstein距離。這些操作本質(zhì)上都可以用最優(yōu)傳輸理論來(lái)解釋,并且加以改進(jìn)。以歐氏距離平方為代價(jià)函數(shù)的最優(yōu)傳輸問(wèn)題歸結(jié)為Brenier理論,并且等價(jià)于凸幾何中的Alexandrov理論,最終歸結(jié)為蒙日-安培方程。

在工程計(jì)算中,我們通常用Alexandrov弱解來(lái)逼近真實(shí)解,我們以前討論過(guò)Alexandrov弱解的存在性和性。
蒙日-安培方程的正則性理論

由Brenier定理,Brenier勢(shì)能函數(shù)為整體Lipschitz,因此幾乎處處可導(dǎo)。我們稱可求導(dǎo)的點(diǎn)為正常點(diǎn)(regular point),不可求導(dǎo)的點(diǎn)為奇異點(diǎn)(singular point),則奇異點(diǎn)集合為零測(cè)度。我們考察每一點(diǎn)處的次微分,


圖2. 最優(yōu)傳輸映射中的奇異點(diǎn)集合,(蘇科華作)。
如圖2所示,目標(biāo)測(cè)度的支集具有兩個(gè)聯(lián)通分支,我們稠密采樣目標(biāo)測(cè)度,表示成定義在兩個(gè)團(tuán)簇上面的狄拉克測(cè)度。我們?nèi)缓笥?jì)算蒙日-安培方程的Alenxandrov解。依隨采樣密度增加,狄拉克測(cè)度弱收斂到目標(biāo)測(cè)度,Alenxandrov解收斂到真實(shí)解。我們看到Brenier勢(shì)能函數(shù)的Alenxandrov解可以表示成一張凸曲面,圖曲面中間有一條脊線(ridge),脊線的投影是最優(yōu)傳輸映射的奇異點(diǎn)集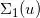

圖3. GPU版本的最優(yōu)傳輸映射(郭洋、Simon Lam 作)。
圖3顯示了基于GPU算法的從平面長(zhǎng)方形上的均勻分布到兩個(gè)半圓盤(pán)上的均勻分布的最優(yōu)傳輸映射,長(zhǎng)方形的中線顯示了最優(yōu)傳輸映射的奇異點(diǎn)集

圖4. GPU版本的最優(yōu)傳輸映射(郭洋、Simon Lam作)。
圖4從平面長(zhǎng)方形上的均勻分布到啞鈴形狀上的均勻分布的最優(yōu)傳輸映射,仔細(xì)觀察,我們可以看出最優(yōu)傳輸映射的奇異點(diǎn)集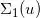 是中線上的兩條線段,介于紅藍(lán)斑點(diǎn)之間。
是中線上的兩條線段,介于紅藍(lán)斑點(diǎn)之間。
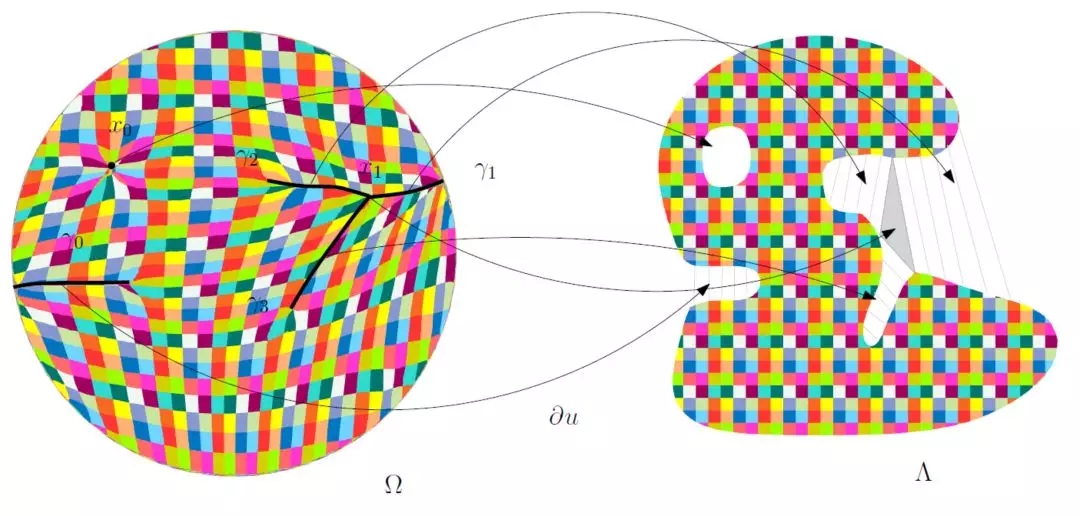
圖5. 最優(yōu)傳輸映射的奇異點(diǎn)結(jié)構(gòu)(齊鑫、蘇科華作)。

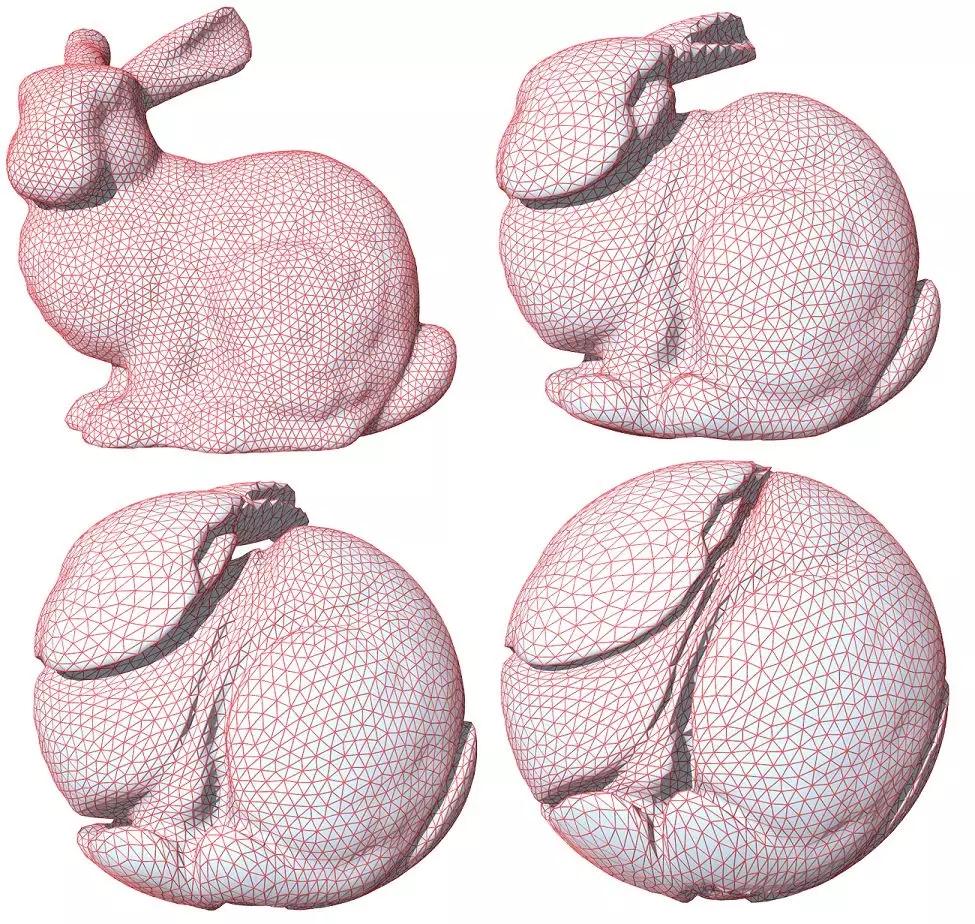
圖6. 實(shí)心兔子和實(shí)心球之間的最優(yōu)傳輸映射,表面皺褶結(jié)構(gòu),(蘇科華作)。
最優(yōu)傳輸映射的奇異點(diǎn)結(jié)構(gòu)理論在高維空間依然成立,如圖6所示,實(shí)心球體和實(shí)心兔子體之間的最優(yōu)傳輸映射誘導(dǎo)了兔子表面上的大量皺褶,最優(yōu)傳輸映射在皺褶處間斷。

模式崩潰的理論解釋
目前的深度神經(jīng)網(wǎng)絡(luò)只能夠逼近連續(xù)映射,而傳輸映射是具有間斷點(diǎn)的非連續(xù)映射,換言之,GAN訓(xùn)練過(guò)程中,目標(biāo)映射不在DNN的可表示泛函空間之中,這一顯而易見(jiàn)的矛盾導(dǎo)致了收斂困難;如果目標(biāo)概率測(cè)度的支集具有多個(gè)聯(lián)通分支,GAN訓(xùn)練得到的又是連續(xù)映射,則有可能連續(xù)映射的值域集中在某一個(gè)連通分支上,這就是模式崩潰(mode collapse);如果強(qiáng)行用一個(gè)連續(xù)映射來(lái)覆蓋所有的連通分支,那么這一連續(xù)映射的值域必然會(huì)覆蓋 之外的一些區(qū)域,即GAN會(huì)生成一些沒(méi)有現(xiàn)實(shí)意義的圖片。這給出了GAN模式崩潰的直接解釋。
之外的一些區(qū)域,即GAN會(huì)生成一些沒(méi)有現(xiàn)實(shí)意義的圖片。這給出了GAN模式崩潰的直接解釋。
那么,如何來(lái)用真實(shí)數(shù)據(jù)驗(yàn)證我們的猜測(cè)呢?我們用CelebA數(shù)據(jù)集驗(yàn)證了傳輸映射的非連續(xù)性。
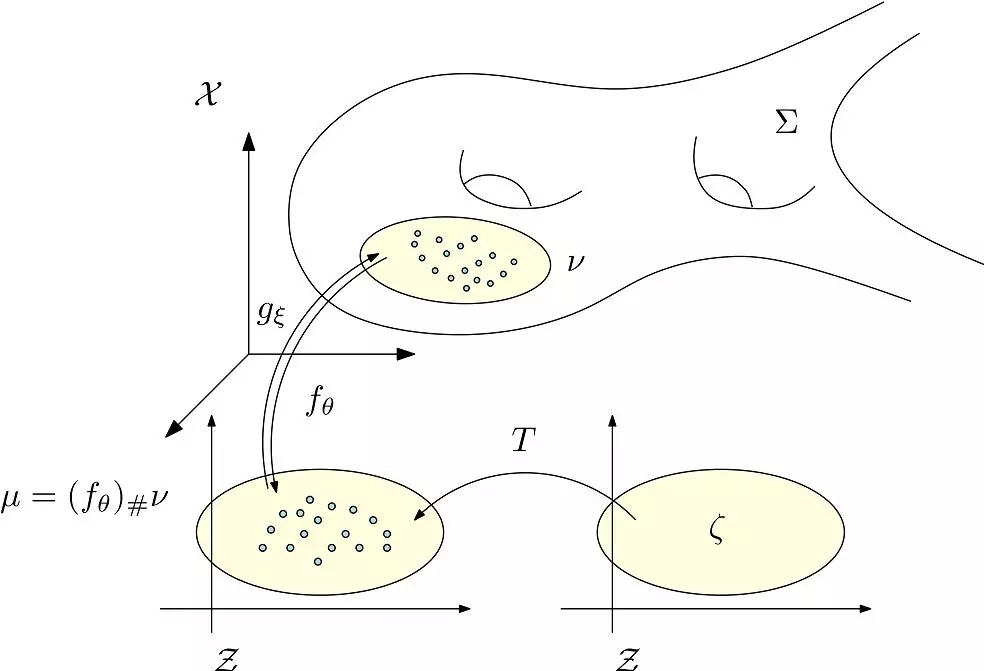
圖7. AE-OT體系結(jié)構(gòu)。


圖8. AE-OT生成的人臉圖像。

圖10. 在隱空間進(jìn)行插值的結(jié)果。

那么如何避免模式崩潰呢?通過(guò)以上分析我們知道,深度神經(jīng)網(wǎng)絡(luò)只能逼近連續(xù)映射,傳輸映射本身是非連續(xù)的,這一內(nèi)在矛盾引發(fā)了模式崩潰。但是最優(yōu)傳輸映射是Brenier勢(shì)能函數(shù)的梯度,Brenier勢(shì)能函數(shù)本身是連續(xù)的,因此深度神經(jīng)網(wǎng)絡(luò)應(yīng)該來(lái)逼近Brenier勢(shì)能函數(shù),而非傳輸映射。更進(jìn)一步,我們應(yīng)該判斷Brenier勢(shì)能函數(shù)的奇異點(diǎn),即圖2中的脊線和圖6中的皺褶。
小結(jié)
基于真實(shí)數(shù)據(jù)的流形分布假設(shè),我們將深度學(xué)習(xí)的主要任務(wù)分解為學(xué)習(xí)流形結(jié)構(gòu)和概率變換兩部分;概率變換可以用最優(yōu)傳輸理論來(lái)解釋和實(shí)現(xiàn)。基于Brenier理論,我們發(fā)現(xiàn)GAN模型中的生成器D和判別器G計(jì)算的函數(shù)彼此可以相互表示,因此生成器和判別器應(yīng)該交流中間計(jì)算結(jié)果,用合作代替競(jìng)爭(zhēng)。Brenier理論等價(jià)于蒙日-安培方程,蒙日-安培方程正則性理論表明:如果目標(biāo)概率分布的支集非凸,那么存在零測(cè)度的奇異點(diǎn)集,傳輸映射在奇異點(diǎn)處間斷。而傳統(tǒng)深度神經(jīng)網(wǎng)絡(luò)只能逼近連續(xù)映射,這一矛盾造成了模式崩潰。
通過(guò)計(jì)算Brenier勢(shì)能函數(shù),并且判定奇異點(diǎn)集,我們可以避免模式崩潰。這些算法存在GPU實(shí)現(xiàn)方式。這種方法更為穩(wěn)定,魯棒,訓(xùn)練效率大為提升,并且用透明的理論模型部分取代了經(jīng)驗(yàn)的黑箱。
References
【1】Na Lei, Yang Guo, Dongsheng An, Xin Qi, Zhongxuan Luo, Shing-Tung Yau, Xianfeng Gu. "Mode Collapse and Regularity of Optimal Transportation Maps", ArXiv:1902.02934
聲明:文章收集于網(wǎng)絡(luò),為傳播信息而發(fā),如有侵權(quán),請(qǐng)聯(lián)系小編及時(shí)處理,謝謝!
歡迎加入本站公開(kāi)興趣群商業(yè)智能與數(shù)據(jù)分析群
興趣范圍包括各種讓數(shù)據(jù)產(chǎn)生價(jià)值的辦法,實(shí)際應(yīng)用案例分享與討論,分析工具,ETL工具,數(shù)據(jù)倉(cāng)庫(kù),數(shù)據(jù)挖掘工具,報(bào)表系統(tǒng)等全方位知識(shí)
QQ群:81035754
文章版權(quán)歸作者所有,未經(jīng)允許請(qǐng)勿轉(zhuǎn)載,若此文章存在違規(guī)行為,您可以聯(lián)系管理員刪除。
轉(zhuǎn)載請(qǐng)注明本文地址:http://specialneedsforspecialkids.com/yun/4847.html
摘要:引用格式王坤峰,茍超,段艷杰,林懿倫,鄭心湖,王飛躍生成對(duì)抗網(wǎng)絡(luò)的研究與展望自動(dòng)化學(xué)報(bào),論文作者王坤峰,茍超,段艷杰,林懿倫,鄭心湖,王飛躍摘要生成式對(duì)抗網(wǎng)絡(luò)目前已經(jīng)成為人工智能學(xué)界一個(gè)熱門的研究方向。本文概括了的研究進(jìn)展并進(jìn)行展望。 3月27日的新智元 2017 年技術(shù)峰會(huì)上,王飛躍教授作為特邀嘉賓將參加本次峰會(huì)的 Panel 環(huán)節(jié),就如何看待中國(guó) AI學(xué)術(shù)界論文數(shù)量多,但大師級(jí)人物少的現(xiàn)...
摘要:特征匹配改變了生成器的損失函數(shù),以最小化真實(shí)圖像的特征與生成的圖像之間的統(tǒng)計(jì)差異。我們建議讀者檢查上使用的損失函數(shù)和相應(yīng)的性能,并通過(guò)實(shí)驗(yàn)驗(yàn)證來(lái)設(shè)置。相反,我們可能會(huì)將注意力轉(zhuǎn)向?qū)ふ以谏善餍阅懿患褧r(shí)不具有接近零梯度的損失函數(shù)。 前 ?言GAN模型相比較于其他網(wǎng)絡(luò)一直受困于三個(gè)問(wèn)題的掣肘:?1. 不收斂;模型訓(xùn)練不穩(wěn)定,收斂的慢,甚至不收斂;?2. mode collapse; 生成器產(chǎn)生的...
摘要:例如,即插即用生成網(wǎng)絡(luò)通過(guò)優(yōu)化結(jié)合了自動(dòng)編碼器損失,損失,和通過(guò)與訓(xùn)練的分類器定于的分類損失的目標(biāo)函數(shù),得到了較高水平的樣本。該論文中,作者提出了結(jié)合的原則性方法。 在機(jī)器學(xué)習(xí)研究領(lǐng)域,生成式對(duì)抗網(wǎng)絡(luò)(GAN)在學(xué)習(xí)生成模型方面占據(jù)著統(tǒng)治性的地位,在使用圖像數(shù)據(jù)進(jìn)行訓(xùn)練的時(shí)候,GAN能夠生成視覺(jué)上以假亂真的圖像樣本。但是這種靈活的算法也伴隨著優(yōu)化的不穩(wěn)定性,導(dǎo)致模式崩潰(mode colla...
摘要:最近老顧收到很多讀者來(lái)信,絕大多數(shù)詢問(wèn)對(duì)抗生成網(wǎng)絡(luò)的最優(yōu)傳輸解釋,以及和蒙日安培方程的關(guān)系。蒙日安培方程的幾何解法硬件友好,可以用目前的并行實(shí)現(xiàn)。蒙日安培方程的正則性理論更加復(fù)雜,但是對(duì)于模式塌縮的理解非常關(guān)鍵。 最近老顧收到很多讀者來(lái)信,絕大多數(shù)詢問(wèn)對(duì)抗生成網(wǎng)絡(luò)的最優(yōu)傳輸解釋,以及和蒙日-安培方程的關(guān)系。很多問(wèn)題涉及到經(jīng)典蒙日-安培方程理論,這里我們從偏微分方程和幾何角度介紹一下蒙日-安培...
摘要:的兩位研究者近日融合了兩種非對(duì)抗方法的優(yōu)勢(shì),并提出了一種名為的新方法。的缺陷讓研究者開(kāi)始探索用非對(duì)抗式方案來(lái)訓(xùn)練生成模型,和就是兩種這類方法。不幸的是,目前仍然在圖像生成方面顯著優(yōu)于這些替代方法。 生成對(duì)抗網(wǎng)絡(luò)(GAN)在圖像生成方面已經(jīng)得到了廣泛的應(yīng)用,目前基本上是 GAN 一家獨(dú)大,其它如 VAE 和流模型等在應(yīng)用上都有一些差距。盡管 wasserstein 距離極大地提升了 GAN 的...
閱讀 1510·2021-11-22 13:52
閱讀 1324·2021-09-29 09:34
閱讀 2723·2021-09-09 11:40
閱讀 3042·2019-08-30 15:54
閱讀 1270·2019-08-30 15:53
閱讀 982·2019-08-30 11:01
閱讀 1371·2019-08-29 17:22
閱讀 1965·2019-08-26 10:57