摘要：在上通過這篇文章快速地介紹了不同類型的卷積結構及優勢。為了簡單起見，本文僅探討二維卷積結構。轉置卷積轉置卷積又名反卷積或是分數步長卷積。反卷積這種叫法是不合適的，因為它不符合反卷積的概念。實際上，反卷積是卷積操作的逆過程。

卷積神經網絡作為深度學習的典型網絡，在圖像處理和計算機視覺等多個領域都取得了很好的效果。

Paul-Louis Pr?ve在Medium上通過這篇文章快速地介紹了不同類型的卷積結構（Convolution）及優勢。為了簡單起見，本文僅探討二維卷積結構。

卷積

首先，定義下卷積層的結構參數。

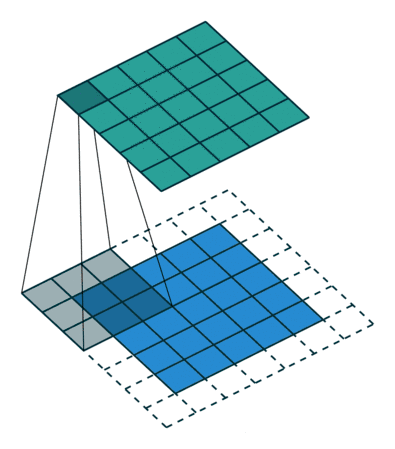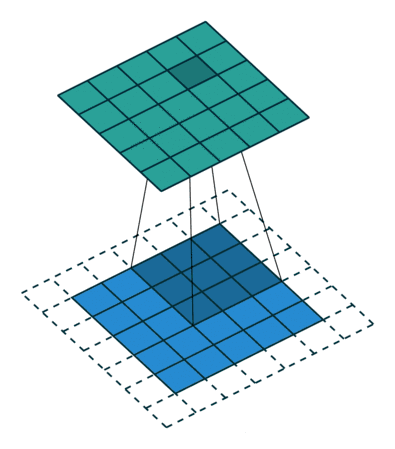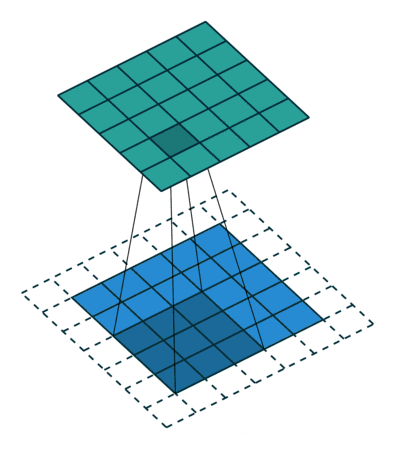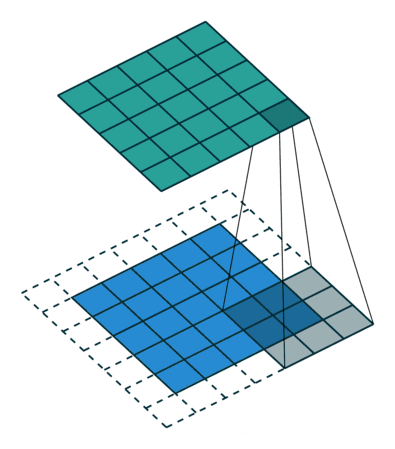
卷積核為3、步幅為1和帶有邊界擴充的二維卷積結構

卷積核大小（Kernel Size）：定義了卷積操作的感受野。在二維卷積中，通常設置為3，即卷積核大小為3×3。

步幅（Stride）：定義了卷積核遍歷圖像時的步幅大小。其默認值通常設置為1，也可將步幅設置為2后對圖像進行下采樣，這種方式與較大池化類似。

邊界擴充（Padding）：定義了網絡層處理樣本邊界的方式。當卷積核大于1且不進行邊界擴充，輸出尺寸將相應縮小；當卷積核以標準方式進行邊界擴充，則輸出數據的空間尺寸將與輸入相等。

輸入與輸出通道（Channels）：構建卷積層時需定義輸入通道I，并由此確定輸出通道O。這樣，可算出每個網絡層的參數量為I×O×K，其中K為卷積核的參數個數。例，某個網絡層有64個大小為3×3的卷積核，則對應K值為 3×3 =9。

空洞卷積

空洞卷積（atrous convolutions）又名擴張卷積（dilated convolutions），向卷積層引入了一個稱為 “擴張率(dilation rate)”的新參數，該參數定義了卷積核處理數據時各值的間距。

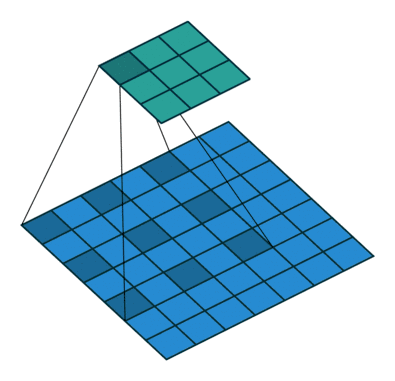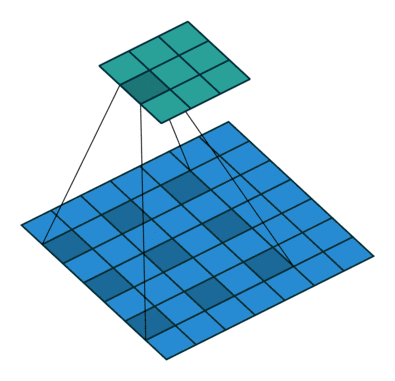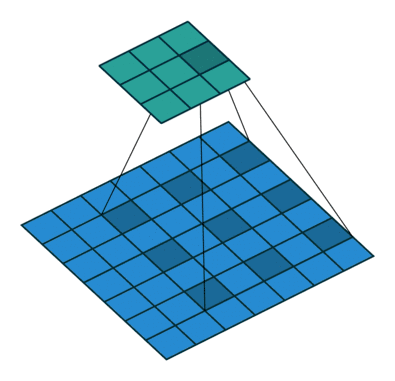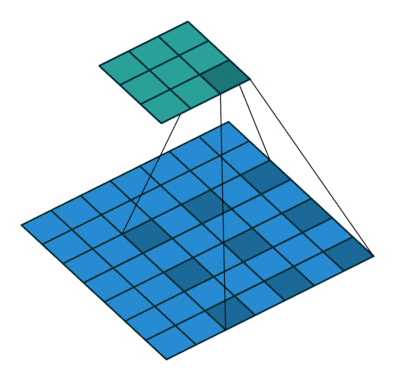
卷積核為3、擴張率為2和無邊界擴充的二維空洞卷積

一個擴張率為2的3×3卷積核，感受野與5×5的卷積核相同，而且僅需要9個參數。你可以把它想象成一個5×5的卷積核，每隔一行或一列刪除一行或一列。

在相同的計算條件下，空洞卷積提供了更大的感受野。空洞卷積經常用在實時圖像分割中。當網絡層需要較大的感受野，但計算資源有限而無法提高卷積核數量或大小時，可以考慮空洞卷積。

轉置卷積

轉置卷積（transposed Convolutions）又名反卷積（deconvolution）或是分數步長卷積（fractially straced convolutions）。

反卷積（deconvolutions）這種叫法是不合適的，因為它不符合反卷積的概念。在深度學習中，反卷積確實存在，但是并不常用。實際上，反卷積是卷積操作的逆過程。你可以這么理解這個過程，將某個圖像輸入到單個卷積層，取卷積層的輸出傳遞到一個黑盒子中，這個黑盒子輸出了原始圖像。那么可以說，這個黑盒子完成了一個反卷積操作，也就是卷積操作的數學逆過程。

轉置卷積與真正的反卷積有點相似，因為兩者產生了相同的空間分辨率。然而，這兩種卷積對輸入數據執行的實際數學運算是不同的。轉置卷積層只執行了常規的卷積操作，但是恢復了其空間分辨率。

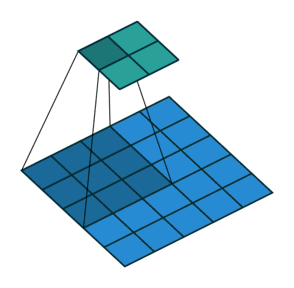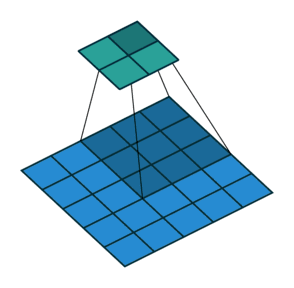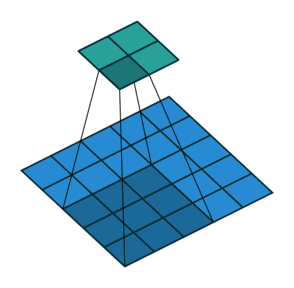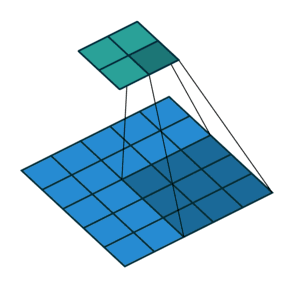
卷積核為3、步幅為2和無邊界擴充的二維卷積結構

舉個例子，假如將一張5×5大小的圖像輸入到卷積層，其中步幅為2，卷積核為3×3，無邊界擴充。則卷積層會輸出2×2的圖像。

若要實現其逆過程，需要相應的數學逆運算，能根據每個輸入像素來生成對應的9個值。然后，將步幅設為2，遍歷輸出圖像，這就是反卷積操作。

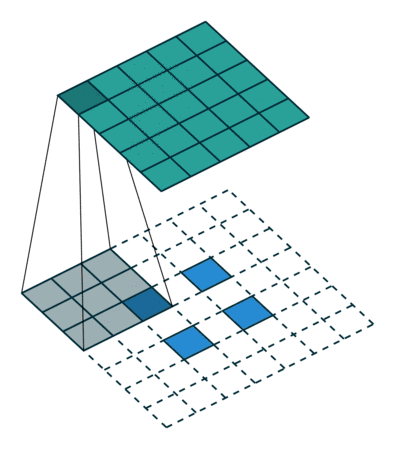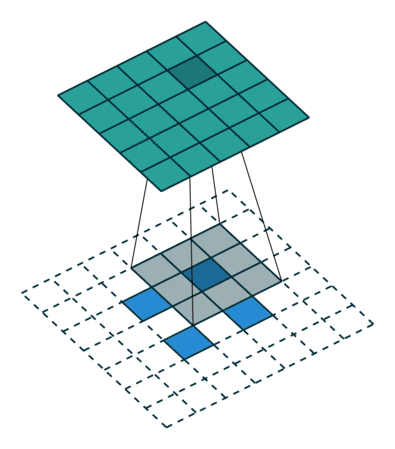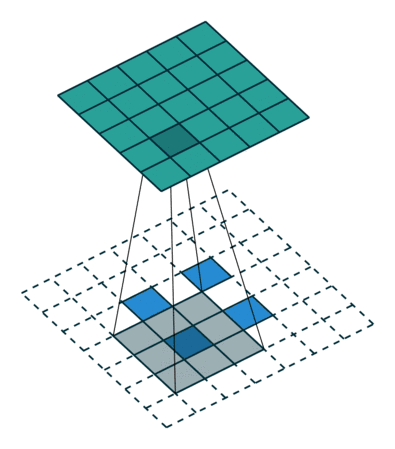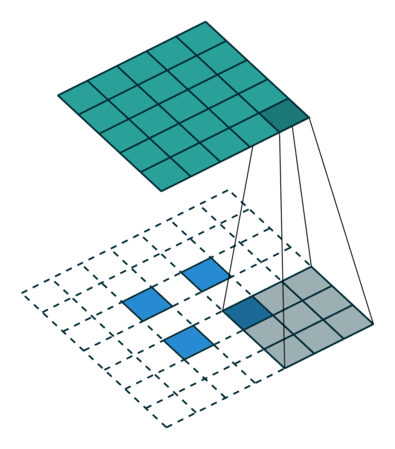
卷積核為3×3、步幅為2和無邊界擴充的二維轉置卷積

轉置卷積和反卷積的共同點在于兩者輸出都為5×5大小的圖像，不過轉置卷積執行的仍是常規的卷積操作。為了實現擴充目的，需要對輸入以某種方式進行填充。

你可以理解成，至少在數值方面上，轉置卷積不能實現卷積操作的逆過程。

轉置卷積只是為了重建先前的空間分辨率，執行了卷積操作。這不是卷積的數學逆過程，但是用于編碼器-解碼器結構中，效果仍然很好。這樣，轉置卷積可以同時實現圖像的粗粒化和卷積操作，而不是通過兩個多帶帶過程來完成。

可分離卷積

在可分離卷積（separable convolution）中，可將卷積核操作拆分成多個步驟。卷積操作用y=conv(x, k)來表示，其中輸出圖像為y，輸入圖像為x，卷積核為k。接著，假設k可以由下式計算得出：k=k1.dot(k2)。這就實現了一個可分離卷積操作，因為不用k執行二維卷積操作，而是通過k1和k2分別實現兩次一維卷積來取得相同效果。

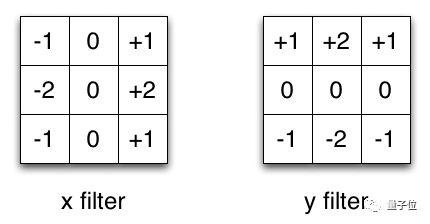
X、Y方向上的Sobel濾波器

Sobel算子通常被用于圖像處理中，這里以它為例。你可以分別乘以矢量[1,0,-1]和[1,2,1]的轉置矢量后得到相同的濾波器。完成這個操作，只需要6個參數，而不是二維卷積中的9個參數。

這個例子說明了什么叫做空間可分離卷積，這種方法并不應用在深度學習中，只是用來幫你理解這種結構。

在神經網絡中，我們通常會使用深度可分離卷積結構（depthwise separable convolution）。

這種方法在保持通道分離的前提下，接上一個深度卷積結構，即可實現空間卷積。接下來通過一個例子讓大家更好地理解。

假設有一個3×3大小的卷積層，其輸入通道為16、輸出通道為32。具體為，32個3×3大小的卷積核會遍歷16個通道中的每個數據，從而產生16×32=512個特征圖譜。進而通過疊加每個輸入通道對應的特征圖譜后融合得到1個特征圖譜。最后可得到所需的32個輸出通道。

針對這個例子應用深度可分離卷積，用1個3×3大小的卷積核遍歷16通道的數據，得到了16個特征圖譜。在融合操作之前，接著用32個1×1大小的卷積核遍歷這16個特征圖譜，進行相加融合。這個過程使用了16×3×3+16×32×1×1=656個參數，遠少于上面的16×32×3×3=4608個參數。

這個例子就是深度可分離卷積的具體操作，其中上面的深度乘數（depth multiplier）設為1，這也是目前這類網絡層的通用參數。

這么做是為了對空間信息和深度信息進行去耦。從Xception模型的效果可以看出，這種方法是比較有效的。由于能夠有效利用參數，因此深度可分離卷積也可以用于移動設備中。

商業智能與數據分析群

興趣范圍包括各種讓數據產生價值的辦法，實際應用案例分享與討論，分析工具，ETL工具，數據倉庫，數據挖掘工具，報表系統等全方位知識

QQ群：81035754