摘要：在學(xué)習(xí)過程中，神經(jīng)網(wǎng)絡(luò)的突觸權(quán)重會(huì)以一種有序的方式進(jìn)行修改，從而實(shí)現(xiàn)所需的目標(biāo)。中間單元的數(shù)量被稱為網(wǎng)絡(luò)所用的片的數(shù)量。

隨著神經(jīng)網(wǎng)絡(luò)的進(jìn)化，許多過去曾被認(rèn)為不可想象的任務(wù)現(xiàn)在也能夠被完成了。圖像識(shí)別、語(yǔ)音識(shí)別、尋找數(shù)據(jù)集中的深度關(guān)系等任務(wù)現(xiàn)在已經(jīng)變得遠(yuǎn)遠(yuǎn)更加簡(jiǎn)單了。在此向這一領(lǐng)域的杰出的研究者致以真誠(chéng)的謝意，正是他們的發(fā)現(xiàn)和成果幫助我們利用上了神經(jīng)網(wǎng)絡(luò)的真正力量。

如果你真正對(duì)追求機(jī)器學(xué)習(xí)這一門學(xué)科感興趣，你必需要對(duì)深度學(xué)習(xí)網(wǎng)絡(luò)有透徹的理解。大部分機(jī)器學(xué)習(xí)算法在處理具有多個(gè)變量的數(shù)據(jù)集時(shí)往往會(huì)有準(zhǔn)確度下降的問題，而深度學(xué)習(xí)模型則能在這些情形中產(chǎn)生「奇跡」。因此，了解深度學(xué)習(xí)模型的工作方式對(duì)我們來說是非常重要的。

在這篇文章中，我會(huì)解釋用于深度學(xué)習(xí)的一些核心概念，即哪些類型的后臺(tái)的計(jì)算導(dǎo)致了模型準(zhǔn)確度的提升。此外，我也會(huì)分享各種建模的技巧，并簡(jiǎn)單論述一下神經(jīng)網(wǎng)絡(luò)的發(fā)展歷史。

目錄

一、神經(jīng)網(wǎng)絡(luò)的歷史

二、單層感知器

三、多層感知器

參數(shù)初始化

激活函數(shù)

反向傳播算法

梯度下降

成本函數(shù)

學(xué)習(xí)率

動(dòng)量

Softmax

多層感知器：總結(jié)

四、深度學(xué)習(xí)概覽

受限玻爾茲曼機(jī)和深度信念網(wǎng)絡(luò)

Dropout

處理類不平衡的技術(shù)

SMOTE：合成少類過采樣技術(shù)

神經(jīng)網(wǎng)絡(luò)中對(duì)成本敏感的學(xué)習(xí)

一、神經(jīng)網(wǎng)絡(luò)的歷史

神經(jīng)網(wǎng)絡(luò)是當(dāng)今深度學(xué)習(xí)領(lǐng)域技術(shù)突破的基石。神經(jīng)網(wǎng)絡(luò)可被看作是一種大規(guī)模并行的簡(jiǎn)單處理單元，它能夠存儲(chǔ)知識(shí)（knowledge）并使用這種知識(shí)來做出預(yù)測(cè)。

神經(jīng)網(wǎng)絡(luò)需要通過學(xué)習(xí)過程來從其環(huán)境中獲取知識(shí)，這個(gè)過程模擬了生物大腦的工作方式。然后，被稱為突觸權(quán)重（synaptic weight）的干涉連接強(qiáng)度可被用于存儲(chǔ)獲取到的知識(shí)。在學(xué)習(xí)過程中，神經(jīng)網(wǎng)絡(luò)的突觸權(quán)重會(huì)以一種有序的方式進(jìn)行修改，從而實(shí)現(xiàn)所需的目標(biāo)。1950 年，神經(jīng)心理學(xué)家 Karl Lashley 發(fā)表了一篇將大腦視作分布式系統(tǒng)的論文。

人們將神經(jīng)網(wǎng)絡(luò)與人腦進(jìn)行比較的另一個(gè)原因是它們的運(yùn)行方式都像是非線性的并行信息處理系統(tǒng)，可以執(zhí)行模式識(shí)別和感知這樣的計(jì)算。因此，這些網(wǎng)絡(luò)在語(yǔ)音、音頻和圖像識(shí)別等本質(zhì)上是非線性的輸入/信號(hào)上可以具有非常良好的表現(xiàn)。

神經(jīng)網(wǎng)絡(luò)先驅(qū) McCulloch 和 Pitts 在 1943 年發(fā)表了一篇對(duì)一個(gè)有兩個(gè)輸入和一個(gè)輸出的模型的研究文章。該模型具有以下特性：

要一個(gè)神經(jīng)元被激活，必需滿足以下條件：

其中一個(gè)輸入是激活的

每個(gè)輸入的權(quán)重相等

該模型的輸出是二元的

通過對(duì)輸入值求和得到的輸出要么是 1，要么是 0；所以這樣的計(jì)算存在一個(gè)特定的閾值。

Hebb 在其 1949 年的著作《The Organization of Behaviour（行為組織）》中第一次提出了這一思想：為了應(yīng)對(duì)任務(wù)的變化，大腦中的連接會(huì)不斷發(fā)生改變。這樣的規(guī)則意味著兩個(gè)神經(jīng)元之間的連接在這同一時(shí)間內(nèi)是激活的。這一思想很快就變成了開發(fā)學(xué)習(xí)的計(jì)算模型和自適應(yīng)系統(tǒng)的靈感來源。

人工神經(jīng)網(wǎng)絡(luò)有能力從被提供的數(shù)據(jù)中學(xué)習(xí)，這被稱為自適應(yīng)學(xué)習(xí)（adaptive learning），而神經(jīng)網(wǎng)絡(luò)創(chuàng)造其自己的組織或信息表征的能力則被稱為自組織（self-organisation）。

15 年后，Rosenblatt 于 1958 年開發(fā)出了感知器（perceptron），成為了神經(jīng)元的下一個(gè)模型。感知器是最簡(jiǎn)單的神經(jīng)網(wǎng)絡(luò)，能將數(shù)據(jù)線性地分為兩類。后來，他隨機(jī)地將這些感知器互相連接，并使用了一種試錯(cuò)方法來改變權(quán)重以進(jìn)行學(xué)習(xí)。

1969 年，在數(shù)學(xué)家 Marvin Minsky 和 Seymour Parpert 發(fā)表了一篇對(duì)感知器的數(shù)學(xué)分析后，這個(gè)方向的研究在接下來的 15 年里陷入了停滯。他們的研究發(fā)現(xiàn)感知器無法表征很多重要的問題，比如異或函數(shù)（XOR）。其實(shí)，那時(shí)的計(jì)算機(jī)還沒有足夠的處理能力來有效地處理大型神經(jīng)網(wǎng)絡(luò)。

1986 年，Rumelhart、Hinton 和 Williams 報(bào)告他們所開發(fā)的反向傳播（back-propagation）算法能夠解決 XOR 這樣的問題，并由此開啟了第二代神經(jīng)網(wǎng)絡(luò)。同一年，Rumelhart 和 McClelland 編輯的兩卷知名著作《Parallel Distributed Processing: Explorations in the Microstructures of Cognition（并行分布式處理：認(rèn)知的微結(jié)構(gòu)中的探索）》發(fā)表。這本書在反向傳播的應(yīng)用上產(chǎn)生了很大的影響，而反向傳播也已經(jīng)在多層感知器的訓(xùn)練上成為了更為流行的學(xué)習(xí)算法。

二、單層感知器（SLP）

感知器的最簡(jiǎn)單形式是在輸入和輸出之間有一個(gè)單層的權(quán)重連接。這種形式可被看作是最簡(jiǎn)單的前饋網(wǎng)絡(luò)（feed-forward network）。在一個(gè)前饋網(wǎng)絡(luò)中，信息總是向一個(gè)方向移動(dòng)，永不回頭。

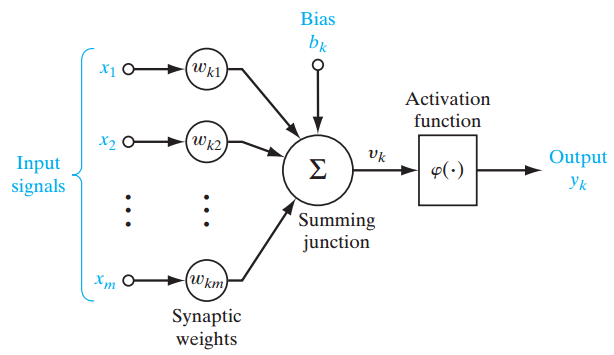
圖 1

圖 1 就是一個(gè)單層感知器，可用來更輕松地理解前面所解釋的多層感知器的概念基礎(chǔ)。單層感知器表示了網(wǎng)絡(luò)中一個(gè)層和其它層之間的連接的 m 權(quán)重，該權(quán)重可被看作是一組突觸或連接鏈。這個(gè)參數(shù)表示了每個(gè)特征 xj 的重要性。下面是輸入乘以它們各自的突觸連接這一功能的加法器函數(shù)：

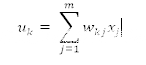
其偏置 bk 用作對(duì)加法器函數(shù) uk 得到 vk 的輸出的仿射變換（ affine transformation），其誘導(dǎo)局部域（induced local field）為：

三、多層感知器（MLP）

多層感知器也被稱為前饋神經(jīng)網(wǎng)絡(luò)（feed-forward neural network），由每一層都完全連接到下一層的層序列組成。

一個(gè)多層感知器在輸入和輸出層之間有一個(gè)或多個(gè)隱藏層，其中每一層都包含多個(gè)通過權(quán)重鏈接彼此互連的神經(jīng)元。輸入層中神經(jīng)元的數(shù)量即為數(shù)據(jù)集中屬性的數(shù)量，輸出層中神經(jīng)元數(shù)量是對(duì)數(shù)據(jù)集的給定類別的數(shù)量。

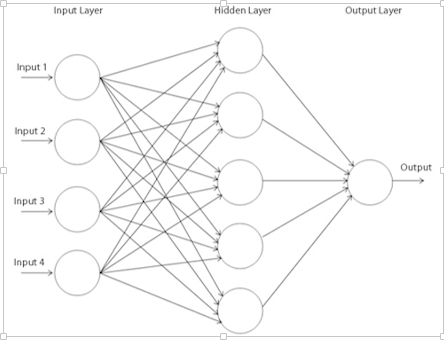
圖2

圖 2 是一個(gè)至少有三層的多層感知器，其中每一層都和前一層相連。要使這個(gè)架構(gòu)做到深度，我們需要引入多個(gè)隱藏層。

參數(shù)的初始化

在參數(shù)的初始化中，權(quán)重（weight）和偏置（bias）在確定最終模型的過程中發(fā)揮了重要的作用。關(guān)于初始化策略的文獻(xiàn)資料有很多。

一個(gè)好的隨機(jī)初始化策略可以避開局部極小值的困境。局部極小值（local minima）問題是指網(wǎng)絡(luò)在訓(xùn)練過程中受困于錯(cuò)誤的表面而不能深入，即使該網(wǎng)絡(luò)還仍有學(xué)習(xí)的能力。

使用不同的初始化策略進(jìn)行實(shí)驗(yàn)已經(jīng)超出了本文的研究范圍。

初始化策略應(yīng)該根據(jù)所使用的激活函數(shù)進(jìn)行選擇。對(duì)于雙曲正切函數(shù)，初始化區(qū)間應(yīng)該為

其中 fan in 是第 i-1 層的單元的數(shù)量，fan out 是第 i 層的單元的數(shù)量。類似地，對(duì)于 S 型激活函數(shù)，初始化區(qū)間應(yīng)該為

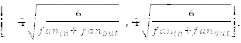
這些初始化策略能在網(wǎng)絡(luò)訓(xùn)練的早期階段確保信息向上和向后傳播。

激活函數(shù)

激活函數(shù)將誘導(dǎo)局部域 v 下的神經(jīng)元的輸出定義為：

其中 φ( ) 是該激活函數(shù)。激活函數(shù)有很多種，下面給出常用的一些：

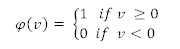
1.閾值函數(shù)（Threshold Function）

上圖表示該神經(jīng)元要么是激活的，要么就是非激活的。但是，該函數(shù)是不可微分的，這在使用反向傳播算法時(shí)非常重要（稍后解釋）。

2. S 型函數(shù)（Sigmoid Function）

和閾值函數(shù)一樣，S 型函數(shù)是一個(gè)取值在 0 到 1 之間的邏輯函數(shù)，但該激活函數(shù)是連續(xù)可微的。

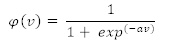
其中 α 是該函數(shù)的斜率參數(shù)（slope parameter）。此外，該函數(shù)在本質(zhì)上是非線性的，這有助于確保權(quán)重和偏置中的較小改變能在神經(jīng)元的輸出中產(chǎn)生較大的變化。

3.雙曲正切函數(shù)（Hyperbolic Tangent Function）

φ(v) = tanh (v)

該函數(shù)可讓激活函數(shù)的取值在 -1 到 +1 之間。

4.修正線性激活函數(shù)（ReLU）

ReLU 是許多邏輯單元之和的平滑近似，能夠產(chǎn)生稀疏的活動(dòng)向量。下面是該函數(shù)的方程式：

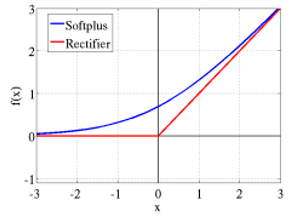
圖3

在圖 3 中

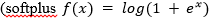
是對(duì)修正器（rectifier）的平滑逼近

5. Maxout 函數(shù)

2013 年，Goodfellow 發(fā)現(xiàn)使用了一種新的激活函數(shù)的 Maxout 網(wǎng)絡(luò)是 dropout 的天然搭檔。

Maxout 單元能促進(jìn) dropout 的優(yōu)化以及提升 dropout 的快速近似模型平均技術(shù)（fast approximate model averaging technique）的準(zhǔn)確度。單個(gè) Maxout 單元可被理解為是對(duì)一個(gè)任意凸函數(shù)的片（piece）形式的線性近似。

Maxout 網(wǎng)絡(luò)不僅能學(xué)習(xí)隱藏單元之間的關(guān)系，還能學(xué)習(xí)每個(gè)隱藏單元的激活函數(shù)。下面是關(guān)于其工作方式的圖形化描述：

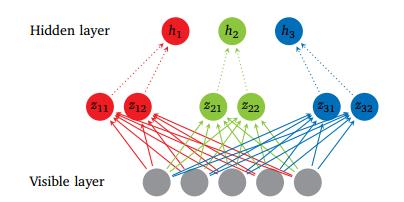
圖4

圖4 展示了帶有 5 個(gè)可見單元、3 個(gè)隱藏單元和每個(gè)隱藏單元 2 個(gè)片的 Maxout 網(wǎng)絡(luò)。

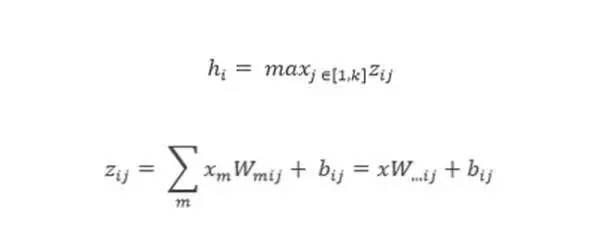
其中 W...ij 是通過獲取矩陣

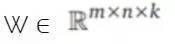
中第二個(gè)坐標(biāo) i 和第三個(gè)坐標(biāo) j 的輸入大小的平均向量。中間單元 k 的數(shù)量被稱為 Maxout 網(wǎng)絡(luò)所用的片（piece）的數(shù)量。

反向傳播算法

反向傳播算法可用于訓(xùn)練前饋神經(jīng)網(wǎng)絡(luò)或多層感知器。這是一種通過改變網(wǎng)絡(luò)中的權(quán)重和偏置來最小化成本函數(shù)（cost function）的方法。為了學(xué)習(xí)和做出更好的預(yù)測(cè)，會(huì)執(zhí)行一些 epoch（訓(xùn)練周期）；在這些 epoch 中，由成本函數(shù)所決定的誤差會(huì)通過梯度下降被反向傳播，直到達(dá)到足夠小的誤差。

梯度下降（Gradient descent）

1.mini-batch 梯度下降

比如說在 100 大小的 mini-batch 中，會(huì)有 100 個(gè)訓(xùn)練樣本被展示給學(xué)習(xí)算法，權(quán)重也會(huì)據(jù)此更新。在所有的 mini-batch 都依次呈現(xiàn)之后，每個(gè) epoch 的準(zhǔn)確度水平和訓(xùn)練成本水平的平均都會(huì)計(jì)算出來。

2.隨機(jī)梯度下降

隨機(jī)梯度下降被用在實(shí)時(shí)在線處理中，其中參數(shù)僅在呈現(xiàn)一個(gè)訓(xùn)練樣本時(shí)才更新，所以準(zhǔn)確度水平和訓(xùn)練成本的平均是從每個(gè) epoch 的整個(gè)訓(xùn)練數(shù)據(jù)集上獲得的。

3.full batch 梯度下降

在這種方法中，所有的訓(xùn)練樣本都會(huì)被展示給學(xué)習(xí)算法，然后再更新權(quán)重。

成本函數(shù)（Cost Function）

成本函數(shù)有很多種，這里給出幾個(gè)例子：

1.均方誤差函數(shù)

其中 yi 是預(yù)測(cè)的輸出，oi 是真實(shí)的輸出。

2.交叉熵函數(shù)

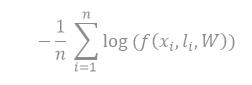
其中 f 函數(shù)是模型在輸入 xi"s 的標(biāo)簽是 li 時(shí)的預(yù)測(cè)概率，W 是它的參數(shù)，n 是訓(xùn)練 batch 的大小。

3.負(fù)對(duì)數(shù)似然損失（NLL）函數(shù)

NLL 是用于本報(bào)告的所有實(shí)驗(yàn)中的成本函數(shù)：

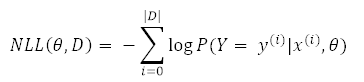
其中 y(i) 是輸出的值，x(i) 是特征輸入的值，θ 是參數(shù)，D 是訓(xùn)練集。

學(xué)習(xí)率（Learning rate）

學(xué)習(xí)率控制著權(quán)重從一次迭代到另一次迭代的變化。一般來說，更小的學(xué)習(xí)率被認(rèn)為是穩(wěn)定的，但學(xué)習(xí)速度也更慢。另一方面，更高的學(xué)習(xí)率可能不穩(wěn)定，會(huì)引起振蕩和數(shù)值誤差，但會(huì)加速學(xué)習(xí)過程。

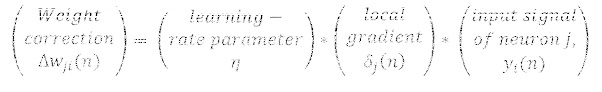
動(dòng)量（Momentum）

動(dòng)量為避免局部極小值提供了慣性；其思想簡(jiǎn)單來說就是為當(dāng)前的權(quán)重更新增加特定比例的先前的權(quán)重更新，這有助于避免受困于局部極小值。

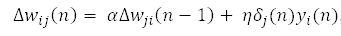
其中 α是動(dòng)量。

Softmax

Softmax 是一種神經(jīng)傳遞函數(shù)，其是可將向量變成概率的輸出層中實(shí)現(xiàn)的 logistic 函數(shù)的廣義形式。這些概率的總和為 1 且限定于 1。

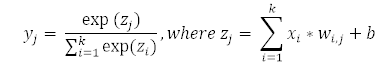
多層感知器（MLP）：總結(jié)

對(duì)于分類任務(wù)，輸出層可能會(huì)整合一個(gè) softmax 函數(shù)用來給出每個(gè)發(fā)生類（occurring class）的概率。激活函數(shù)使用輸入、權(quán)重和偏置在每個(gè)層中計(jì)算每個(gè)神經(jīng)元的預(yù)測(cè)輸出。

反向傳播方法一種訓(xùn)練多層神經(jīng)網(wǎng)絡(luò)的方法，該方法通過修改層之間的突觸連接權(quán)重以在糾錯(cuò)學(xué)習(xí)函數(shù)（需要是連續(xù)可微的）的基礎(chǔ)上提升模型的性能。以下的參數(shù)在本實(shí)驗(yàn)中進(jìn)行了評(píng)估：

隱藏層的數(shù)量

隱藏層中神經(jīng)元的數(shù)量

學(xué)習(xí)率和動(dòng)量

激活函數(shù)的類型

四、深度學(xué)習(xí)概覽

在 2006 年之前，有各種各樣的訓(xùn)練深度監(jiān)督前饋神經(jīng)網(wǎng)絡(luò)的失敗嘗試是由在不可見的數(shù)據(jù)上的性能的過擬合導(dǎo)致的；即在訓(xùn)練誤差降低的同時(shí)驗(yàn)證誤差卻在增長(zhǎng)。

深度網(wǎng)絡(luò)通常是指擁有超過 1 個(gè)隱藏層的人工神經(jīng)網(wǎng)絡(luò)。訓(xùn)練深度隱藏層許多更多算力。更深似乎是更好的，因?yàn)橹庇^上來說，神經(jīng)元可以利用其下面的層中的神經(jīng)元所得出的結(jié)果，這可以得到數(shù)據(jù)的分布式表征。

Bengio 認(rèn)為隱藏層中的神經(jīng)元可被看作是其下面的層中的神經(jīng)元所學(xué)到的特征檢測(cè)器（feature detector）。這個(gè)結(jié)果處于作為一個(gè)神經(jīng)元子集的更好泛化（generalization）中，而這個(gè)神經(jīng)元子集可從輸入空間中的特定區(qū)域的數(shù)據(jù)上進(jìn)行學(xué)習(xí)。

此外，更深度的架構(gòu)可以更加高效，因?yàn)楸憩F(xiàn)相同的功能所需的計(jì)算單元更少，從而能實(shí)現(xiàn)更高的效率。分布式表征背后的核心思想是統(tǒng)計(jì)優(yōu)勢(shì)的共享，其中該架構(gòu)的不同組件會(huì)根據(jù)不同的目的而被復(fù)用。

深度神經(jīng)架構(gòu)是由多個(gè)利用非線性操作的層組成的，例如在帶有許多隱藏層的神經(jīng)網(wǎng)絡(luò)中。數(shù)據(jù)集中常常存在各種變化的因素，例如數(shù)據(jù)各自的性質(zhì)經(jīng)常可能獨(dú)立地變化。

深度學(xué)習(xí)算法可以獲取解釋數(shù)據(jù)中統(tǒng)計(jì)變化的因素和它們交互的方式，從而生成我們觀察的那種類型的數(shù)據(jù)。較低層次的抽象更直接依賴于特定的觀察；而更高層次的也更抽象，因?yàn)樗鼈兏兄獢?shù)據(jù)的連接也更加遙遠(yuǎn)。

深度架構(gòu)學(xué)習(xí)的重點(diǎn)是自動(dòng)發(fā)現(xiàn)這樣的抽象——從低水平的特征到更高水平的概念。可以預(yù)期，這樣的學(xué)習(xí)算法可以在沒有人工定義必要的抽象的情況下進(jìn)行這樣的發(fā)現(xiàn)。

數(shù)據(jù)集中的訓(xùn)練樣本的多樣性必須至少和測(cè)試集一樣，否則學(xué)習(xí)算法就不能歸納。深度學(xué)習(xí)方法的目的是學(xué)習(xí)特征層次，將更低層次的特征組成更高水平的抽象。

帶有大量參數(shù)的深度神經(jīng)網(wǎng)絡(luò)是非常強(qiáng)大的機(jī)器學(xué)習(xí)系統(tǒng)。但是，過擬合（over-fitting）是深度網(wǎng)絡(luò)的一個(gè)嚴(yán)峻難題。過擬合是指當(dāng)驗(yàn)證誤差開始增長(zhǎng)時(shí)，訓(xùn)練誤差卻在下降。Dropout 是一種用于解決這一問題的正則化技術(shù)，將在后面介紹。

今天深度學(xué)習(xí)技術(shù)成功增長(zhǎng)的兩個(gè)最重要因素的其中之一是計(jì)算算力的進(jìn)步。圖形處理單元（GPU）和云計(jì)算對(duì)深度學(xué)習(xí)在許多問題上的應(yīng)用是至關(guān)重要的。

云計(jì)算可實(shí)現(xiàn)計(jì)算機(jī)的集群和按需處理，這有助于通過并行化神經(jīng)網(wǎng)絡(luò)的訓(xùn)練來減少訓(xùn)練時(shí)間。另一方面，GPU 是為高性能數(shù)學(xué)計(jì)算設(shè)計(jì)的專用芯片，可以加速矩陣的計(jì)算。

在 2006-2007 年間，有三篇論文對(duì)深度學(xué)習(xí)這一學(xué)科產(chǎn)生了革命性的影響。他們的成果的關(guān)鍵原理是每一層都可通過無監(jiān)督學(xué)習(xí)的方式進(jìn)行預(yù)訓(xùn)練，一次處理一層。最后，使用誤差的反向傳播的監(jiān)督訓(xùn)練可被用于較精確調(diào)節(jié)所有的層，使得這種通過無監(jiān)督學(xué)習(xí)進(jìn)行的初始化比隨機(jī)初始化更好。

受限玻爾茲曼機(jī)和深度信念網(wǎng)絡(luò)

受限玻爾茲曼機(jī)（RBM）是一種無監(jiān)督算法，可被用于預(yù)訓(xùn)練深度信念網(wǎng)絡(luò)。RBM 是玻爾茲曼機(jī)的簡(jiǎn)化版本，受到了統(tǒng)計(jì)力學(xué)的啟發(fā)。這種方法是基于給定數(shù)據(jù)的潛在分布的概率對(duì)能量（ energy）建模，這些給定的數(shù)據(jù)集來自可以派生出的條件分布。

玻爾茲曼機(jī)是隨機(jī)處理可見單元和隱藏單元的雙向連接網(wǎng)絡(luò)。其原始數(shù)據(jù)（ raw data）對(duì)應(yīng)于「可見」神經(jīng)元和被觀察狀態(tài)的樣本，而且特征檢測(cè)器對(duì)應(yīng)于「隱藏」神經(jīng)元。在玻爾茲曼機(jī)中，可見神經(jīng)元為網(wǎng)絡(luò)和其所在的操作環(huán)境提供輸入。在訓(xùn)練過程中，可見神經(jīng)元受到了鉗制（調(diào)到固定值，由訓(xùn)練數(shù)據(jù)確定）。另一方面，隱藏神經(jīng)元自由運(yùn)行。

然而，玻爾茲曼機(jī)因?yàn)槠溥B通性而非常難以訓(xùn)練。一個(gè) RBM 限制了連通性從而使得學(xué)習(xí)變得簡(jiǎn)單。在組成二分圖（bipartite graph）的單層中，隱藏單元沒有連接，如圖 2。它的優(yōu)勢(shì)是隱藏單位可以獨(dú)立更新，并且與給定的可見狀態(tài)平行。

這些網(wǎng)絡(luò)受到了一個(gè)能量函數(shù)的管控，它決定了隱藏/可見狀態(tài)的概率。隱藏/可見單位的每個(gè)可能的連接結(jié)構(gòu)（ joint configurations ）都有一個(gè)由權(quán)重和偏差決定的 Hopfield 能量。連接結(jié)構(gòu)的能量由吉布斯采樣優(yōu)化，它可通過最小化 RBM 的較低能量函數(shù)學(xué)習(xí)參數(shù)。

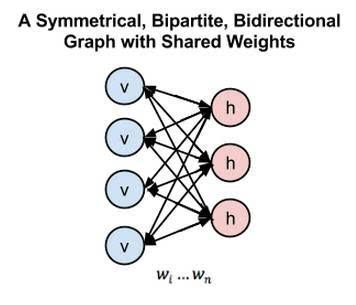
圖5

在圖 5 中，左邊的層表示可見層，而右邊的層表示隱藏層

在深度信念網(wǎng)絡(luò)（DBN）中，RBM 是通過帶有重要特征的輸入數(shù)據(jù)進(jìn)行訓(xùn)練的，這些輸入數(shù)據(jù)是由隱藏層中的隨機(jī)神經(jīng)元獲取的。在第二層，訓(xùn)練特征的激活（activation）被當(dāng)作輸入數(shù)據(jù)處理。第二層 RBM 層中的學(xué)習(xí)過程可被看作是學(xué)習(xí)特征的特征，每次當(dāng)一個(gè)新的層被添加到深度信念網(wǎng)絡(luò)中時(shí)，原始訓(xùn)練數(shù)據(jù)的對(duì)數(shù)概率上的可變的更低的界限就會(huì)獲得提升。

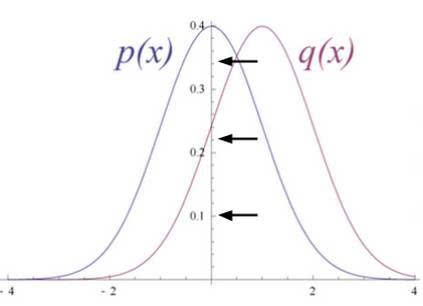
圖6

圖6 展示了 RBM 將它的數(shù)據(jù)分布轉(zhuǎn)變成了隱藏單元上更后面的分布

RBM 的權(quán)重是被隨機(jī)初始化的，造成了分布中 p(x) 和 q(x) 的不同。在學(xué)習(xí)過程中，權(quán)重被迭代調(diào)整，從而最小化 p(x) 和 q(x) 之間的誤差。在圖 2 中，q(x)是源數(shù)據(jù)的近似，p(x) 是源數(shù)據(jù)。

調(diào)整來自一個(gè)神經(jīng)元和其他神經(jīng)元的突觸權(quán)重的原則不受是否是隱藏還是可見神經(jīng)元的支配。通過 RBM 層更新的參數(shù)可被用于 DBN 的初始值，DBN 可通過反向傳播的監(jiān)督訓(xùn)練精調(diào)所有的層。

在 KDD Cup 1999 的 IDS 數(shù)據(jù)上，適合使用多模態(tài)（Bernoulli-Gaussian）RBM 作為包含混合數(shù)據(jù)類型的 KDD Cup 1999，這些數(shù)據(jù)類型特別連續(xù)且明確。在多模態(tài) RBM 中，有兩個(gè)不同的信道輸入層，一個(gè)用于連續(xù)特征的高斯輸入單元，另一個(gè)是其中使用到了二元特征的 Bernoulli 輸入單元層。多模態(tài) RBM 的使用不在本文的討論范圍之中。

DROPOUT

近期的一些進(jìn)展已經(jīng)引入了強(qiáng)大的正則化矩陣（regularizers）來減少神經(jīng)網(wǎng)絡(luò)的過擬合。在機(jī)器學(xué)習(xí)中，正則化是附加信息，通常作為一種懲罰機(jī)制被引入——懲罰導(dǎo)致過擬合的模型的復(fù)雜性。

Dropout 是 Hinton 引入的一種深度神經(jīng)網(wǎng)絡(luò)的正則化技術(shù)，通過在每一個(gè)訓(xùn)練迭代上隨機(jī)關(guān)掉一部分神經(jīng)元，而是在測(cè)試時(shí)間使用整個(gè)網(wǎng)絡(luò)（權(quán)重按比例縮小），從而防止特征檢測(cè)器的共適應(yīng)。

Dropout 通過等同于訓(xùn)練一個(gè)共享權(quán)重的指數(shù)模型減少過擬合。對(duì)于給定的訓(xùn)練迭代，存在不同 dropout 配置的不同指數(shù)，所以幾乎可以肯定每次訓(xùn)練出的模型都不一樣。在測(cè)試階段，使用了所有模型的平均值，作為強(qiáng)大的總體方法。

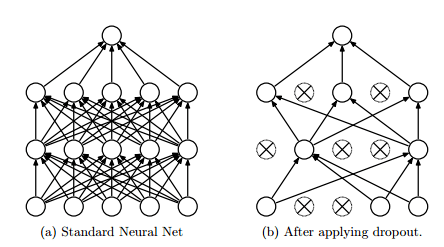
圖 7

圖 7 中，dropout 隨機(jī)舍棄神經(jīng)網(wǎng)絡(luò)層級(jí)之間的連接

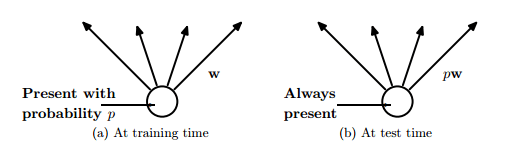
圖 8

圖 8 中，在訓(xùn)練時(shí)間，連接有一定的概率被舍棄，同時(shí)在訓(xùn)練時(shí)間中權(quán)重按比例縮小到 ρw

在很多機(jī)器學(xué)習(xí)競(jìng)賽中，平均眾多模型（Averaging many model）總是獲勝的關(guān)鍵。很多不同類型的模型被使用，然后結(jié)合起來在測(cè)試階段做預(yù)測(cè)。

隨機(jī)森林是一個(gè)非常強(qiáng)大的 bagging 算法，它是通過平均很多決策樹，給它們不同的帶有重置的訓(xùn)練樣本集創(chuàng)造的。眾所周知，決策樹非常容易擬合數(shù)據(jù)，而且在測(cè)試時(shí)間進(jìn)行得非常快，所以通過給它們不同的訓(xùn)練集來平均不同的決策樹是負(fù)擔(dān)得起的。

然而，使用同樣的深度神經(jīng)網(wǎng)絡(luò)方法的計(jì)算成本是非常昂貴的。訓(xùn)練多帶帶的神經(jīng)網(wǎng)絡(luò)和多種神經(jīng)網(wǎng)絡(luò)的成本已經(jīng)很高了，再平均它們看起來是不現(xiàn)實(shí)的。此外，我們需要的是在測(cè)試時(shí)間有效的單個(gè)網(wǎng)絡(luò)，而不是有大量的大型神經(jīng)網(wǎng)絡(luò)。

Dropout 是平均很多大型神經(jīng)網(wǎng)絡(luò)的有效方式。每次訓(xùn)練模型的隱藏單元的時(shí)候都能像圖 8 中那樣以一定的概率漏掉一些。這個(gè)概率通常是 ρ=0.5 時(shí)。因此，帶有減半的開支權(quán)重（outgoing weight）的「平均網(wǎng)絡(luò)」模型可以在測(cè)試時(shí)間像圖 4 中那樣使用。平均網(wǎng)絡(luò)等同于采用概率分布的幾何平均數(shù)，該分布是通過所有帶有單隱層單位和 Softmax 輸出層的網(wǎng)絡(luò)進(jìn)行標(biāo)記預(yù)測(cè)的。

依照數(shù)學(xué)證明 dropout 如何可被視為一個(gè)集成方法：

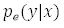
是總效果的預(yù)測(cè)，使用幾何平均數(shù)。

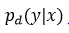
是單個(gè)子模型的預(yù)測(cè)。

d 是區(qū)分將哪個(gè)輸入包括到 softmax 分類器中的二元向量。

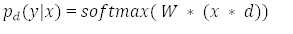
假設(shè)有不同的單元，將會(huì)有 2^N 的可能分配到 d。

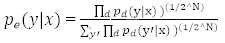
其中 y 是單個(gè)的，也是類目錄（class index）的向量。

由單個(gè)子模型輸出的概率綜合被用于正則化。

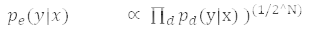
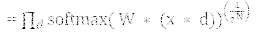
依照 softmax 的定義

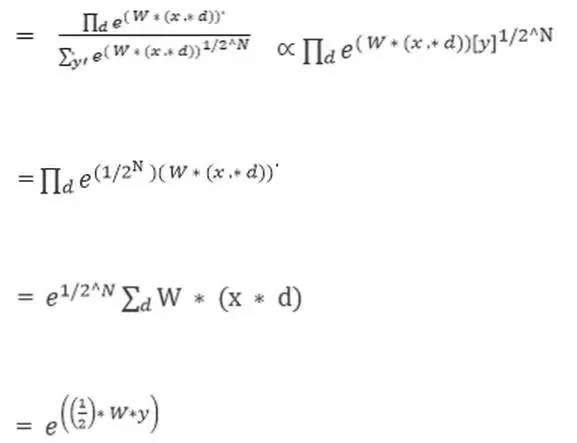
所以預(yù)測(cè)概率肯定與這成比例。為了重新正則化上面的表述，它被

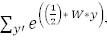
相除，這意味概率分布是

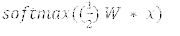
另一種看待 dropout 的方式是，它能防止特征檢測(cè)器間的共適應(yīng)（co-adaption）。特征檢測(cè)器間的共適應(yīng)意味著如果一個(gè)隱藏單位知道其他隱藏單位所代表的內(nèi)容，它就能在訓(xùn)練數(shù)據(jù)上與它們共適應(yīng)。然而，在測(cè)試數(shù)據(jù)集上復(fù)雜的共適應(yīng)可能會(huì)難以泛化。

Dropout 也能以一種低概率應(yīng)用于輸入層，典型的是 20% 的概率。這里的概念和降噪自動(dòng)編碼器發(fā)展出的概念相同。在此方法中，一些輸入會(huì)被遺漏。這會(huì)對(duì)準(zhǔn)確性造成傷害，但也能改善泛化能力，其方式類似于在訓(xùn)練時(shí)將噪聲添加到數(shù)據(jù)集中。

在 2013 年 dropout 的一個(gè)變體出現(xiàn)，叫做 Drop connect。它不再是以特定的概率權(quán)重舍棄隱藏單位，而是以一定的概率隨機(jī)舍棄。在 MNIST 數(shù)據(jù)集上，看起來 Drop connect 網(wǎng)絡(luò)的表現(xiàn)要比 dropout 好。

處理類別不均衡問題的技術(shù)

當(dāng)一個(gè)類別（少數(shù)類）相比于其他類別（多數(shù)類）明顯代表性不足的時(shí)候就會(huì)產(chǎn)生類別不均衡問題。這個(gè)難題有著現(xiàn)實(shí)意義，會(huì)對(duì)誤分類少數(shù)類造成極高的代價(jià)，比如檢測(cè)欺詐或入侵這樣的異常活動(dòng)。這里有多種技術(shù)可以處理類別不均衡難題，如下面解釋的這一種：

SMOTE：合成少數(shù)類過采樣技術(shù)（Synthetic Minority Over-sampling Technique）

解決類別不均衡問題的一個(gè)普遍使用的方法是數(shù)據(jù)集的重新采樣。采樣方法包含預(yù)處理和通過調(diào)整少數(shù)類和多數(shù)類的先驗(yàn)分布均衡訓(xùn)練數(shù)據(jù)集。SMOTE 是一種過采樣方法，其中少數(shù)類通過創(chuàng)造「合成」樣本過采樣，而非通過替換（replacement）進(jìn)行過采樣。

已經(jīng)有人提出說通過替換進(jìn)行的少數(shù)類過采樣不能顯著改進(jìn)結(jié)果，不如說它趨于過擬合少數(shù)類的分類。SMOTE 算法反而是在「特征空間」進(jìn)行操作，而非「數(shù)據(jù)空間」。它通過過采樣少數(shù)類創(chuàng)造合成樣本，這能更好地泛化。

這一思路受到了通過在真實(shí)數(shù)據(jù)上操作創(chuàng)造額外訓(xùn)練數(shù)據(jù)的啟發(fā)，以便于有更多的數(shù)據(jù)幫助概括歸納預(yù)測(cè)。

在此算法中第一個(gè)最近鄰（neighbours）是為了少數(shù)類計(jì)算的。然后，就可以以下列方式計(jì)算少數(shù)類的合成特征：選擇最鄰近的一個(gè)隨機(jī)數(shù)字，然后使用這一數(shù)字與原始少數(shù)類數(shù)據(jù)點(diǎn)的距離。

這一距離乘以 0 和 1 之間的一個(gè)隨機(jī)數(shù)字，然后將結(jié)果增加到原始少數(shù)類數(shù)據(jù)的特征向量中作為一個(gè)額外的樣本，如此就創(chuàng)造出了合成少數(shù)類樣本。

神經(jīng)網(wǎng)絡(luò)中的成本敏感學(xué)習(xí)

成本敏感性學(xué)習(xí)似乎是一種解決分類問題中類別不均衡的相當(dāng)有效的方式。特定于神經(jīng)網(wǎng)絡(luò)的三種成本敏感方法已經(jīng)做了介紹。

在測(cè)試未見過的樣本時(shí)，整合神經(jīng)網(wǎng)絡(luò)輸出層中類別的先驗(yàn)概率

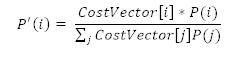
基于成本調(diào)整學(xué)習(xí)率。更好的學(xué)習(xí)率應(yīng)該被分配給有著高誤分類（misclassification）成本的樣本，為這些樣本在權(quán)重變化上產(chǎn)生更大的影響

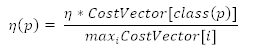
修改均方誤差函數(shù)。結(jié)果是，反向傳播完成的學(xué)習(xí)將最小化誤分類成本，新的誤差函數(shù)是：

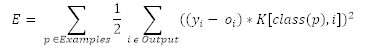
其成本因子是 K[i,j]。

新的誤差函數(shù)會(huì)引出一個(gè)用于更新網(wǎng)絡(luò)權(quán)重的新德爾塔定律

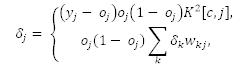
其中第一個(gè)等式代表輸出神經(jīng)元的誤差函數(shù)，第二個(gè)等式代表隱層神經(jīng)元的誤差函數(shù)。

商業(yè)智能與數(shù)據(jù)分析群

興趣范圍包括各種讓數(shù)據(jù)產(chǎn)生價(jià)值的辦法，實(shí)際應(yīng)用案例分享與討論，分析工具，ETL工具，數(shù)據(jù)倉(cāng)庫(kù)，數(shù)據(jù)挖掘工具，報(bào)表系統(tǒng)等全方位知識(shí)

QQ群：81035754