資訊專欄INFORMATION COLUMN

摘要:梯度下降算法梯度是個啥我想最開始接觸梯度的各位是在方向導數那一章接觸這一概念的,如果老師沒怎么講的話可能有些人還不知道梯度是個向量。在二維條件下,因為有了兩個偏導數,所以這個向量能表示一圈。
講你肯定能懂的機器學習多維極值求解
事先說明
本文面向學習過高等數學統計學和線性代數基礎知識的本科生,并假設讀者擁有基本的矩陣運算和求導運算的相關知識,類似梯度,方向導數、Hessian Matrix這些東西不懂也沒關系,我會用盡可能通俗的語言說明運算中的意義。
那么從最簡單的開始。
梯度下降算法
梯度是個啥?我想最開始接觸梯度的各位是在方向導數那一章接觸這一概念的,如果老師沒怎么講的話可能有些人還不知道梯度是個向量。當你學梯度的時候,所有的概念全都是在二元函數下的,well,也寫想象力不是很豐富的同學可能不知道這是個啥。來,我們降維先。
多維條件下是曲面對函數的一階偏導數向量,那么在一維條件下梯度會是什么的?顯然就木有偏導數了,只有一個東西,當然你也可以把它寫成向量的形式,就是一個導數,只不過現在變成一維的了,所以方向只有倆,向左和向右。值為正的時候向右,值為負的時候向左,值大值小不影響方向只影響距離。
在二維條件下,因為有了兩個偏導數,所以這個向量能表示一圈。如果你以前看過些文章或者視頻或者什么ppt之類的東西,大概你會聽說一種說法:“梯度是曲面中最陡峭的方向,這個方向是下降最快的方向。”實際上這種說法是不準確的,從一維的角度來看,“梯度”其實是上升最快的方向,比如
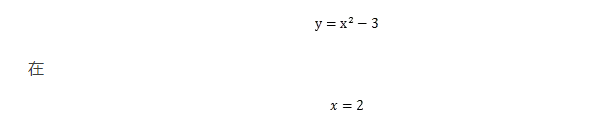
處的導數是1,方向向右,這個方向函數是增長的。同樣二維也是如此。只不過大部分迭代公式中在梯度的前面會加一個負號,比如這個
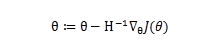
。所以也就直接認為它代表了下降最快的方向了。
直觀上,你可以理解為,梯度就是一個和曲面等高線垂直的法線,沖著增高的那邊。就像下圖:
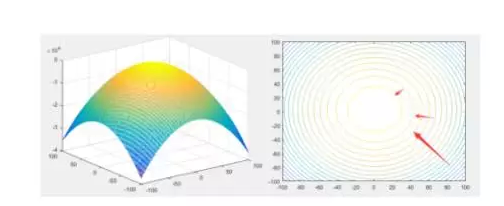
那么它相反的方向就是下降的方向啦,函數的極值點導數都是0的,也就是說,你沿著梯度方向一直走,如果最終收斂到一個點,那肯定就是一個極值點,如果不收斂,說明可能不存在極值點哈(這里因為有步長的涉及,在求解的時候會遇到明明有極值點卻沒有收斂的問題,后面會提到)。
舉個例子,在一維下用梯度下降算法求解極值點的問題。這里我先舉一個方便驗算的例子,方便大家理解。

,這里 就是步長,用來調節每一次移動的距離,你也可能聽過一些 不能過大也不能過小的看起來只能靠經驗的廢話。如果你是剛剛入門,可能寫點程序,然后不斷試,但是實際上 較優的也是可以算的,只不過那又是另一門帶有好多論文的學科了。
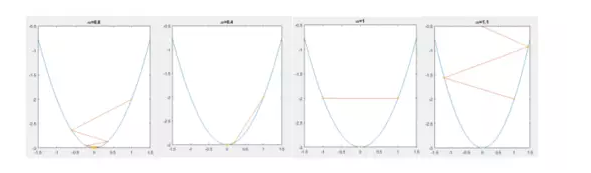
不同的 得到不一樣的迭代效果,收斂或者震蕩收斂,周期震蕩或者直接發散,但是有的時候,算一遍
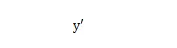
很費勁啊!這里例子簡單,要是碰到TB級的數據那真的是要死了。這還能去試?這里簡單的說一下怎么設置 ,首先你要確定x是收斂的。所以公式

實際上如果 控制在0到1/2之間會收斂更快,因為震蕩收斂總會造成一些重復計算。
二維上的梯度下降能干啥呢?
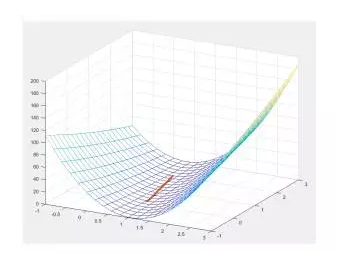
還是舉一個簡單的例子,這里直接連數據都是最簡單的。你有兩個點(4,4),(6,5),你想畫一條線使得線和兩個點之間的距離平方和最小,當然你也可以口算出來,但是我們依然是為了看一下作用,直接寫公式對于一些人來說真的會蒙。


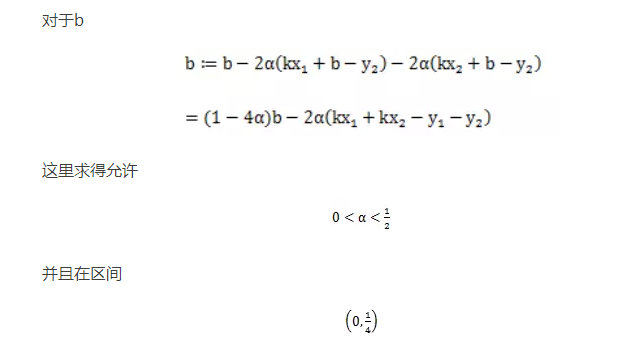
內不會震蕩,梯度計算方向在二維曲面震蕩起來長啥樣啊。來來來畫個圖。開始震蕩的部分我想我得給他個特寫。
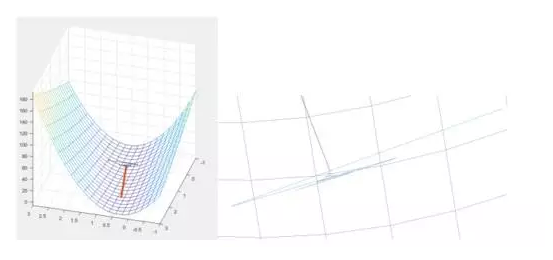
不過癮?來看這個
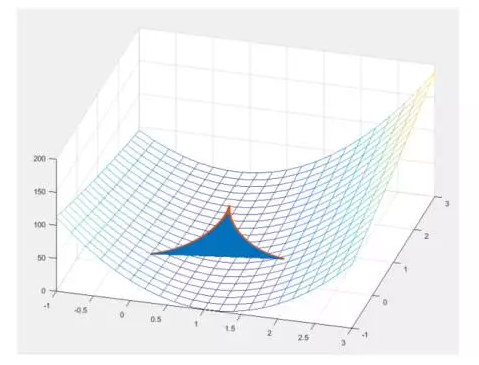
大致知道啥意思就行了哈。
在不震蕩的情況下就顯得特別簡潔了。一條線走回去。
當然教科書上數學書上肯定不會這么寫例子,為了公式的簡潔,最后改為:

了, 則表示所有參數的集合。咦?公式多了個1/2是哪來的?在這里實際上這個值是多少都無所謂,因為兩個偏導數都帶著這個1/2不影響梯度方向,只影響步長,而步長又可以由調節,我們可以理解為,加了它,導數寫起來好看^_^。就像下面這樣。
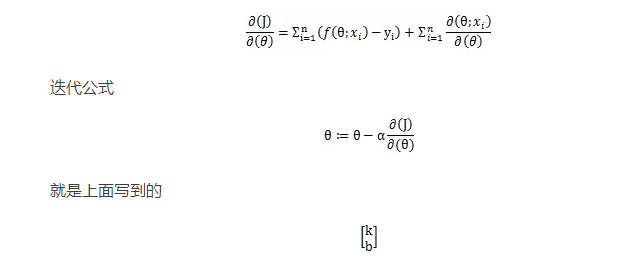
一個列向量。
更多維的原理都一樣,梯度下降就講到這。
牛頓法
提到牛頓法的時候,你可能在小的時候聽說過,一個用來迭代求零點的方法,稍微提一下。

,然后不斷的試值,唔~~還是來畫圖吧。
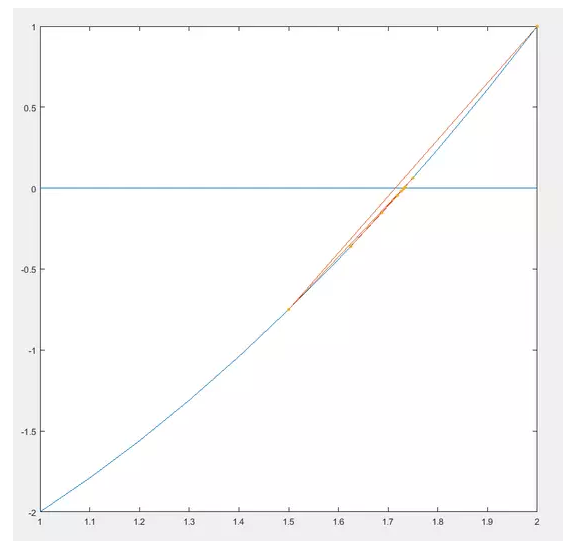
你也可以看到他們的迭代過程,當然這個不叫牛頓法,這個叫二分法,比較low哈,看到沒,震蕩了,震蕩收斂慢。

當趨近于0的時候他倆才近似。而牛頓法就是用切線來快速逼近零點的,不會震蕩呦,畫圖吧先。
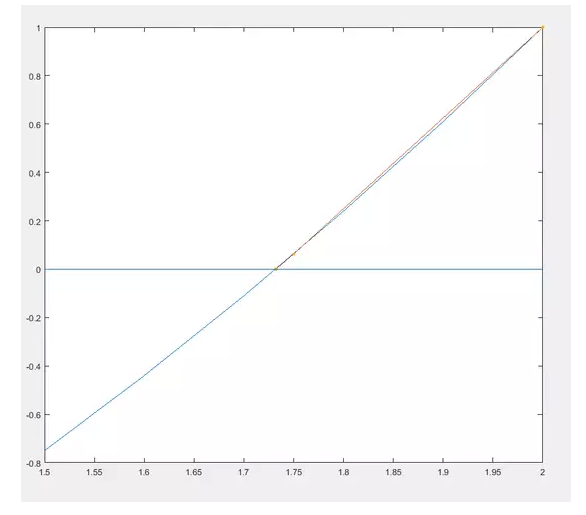
看起來兩步就收斂了啊,好厲害,怎么做到不震蕩的呢它?
因為每一步迭代移動切線與x軸交叉點的距離
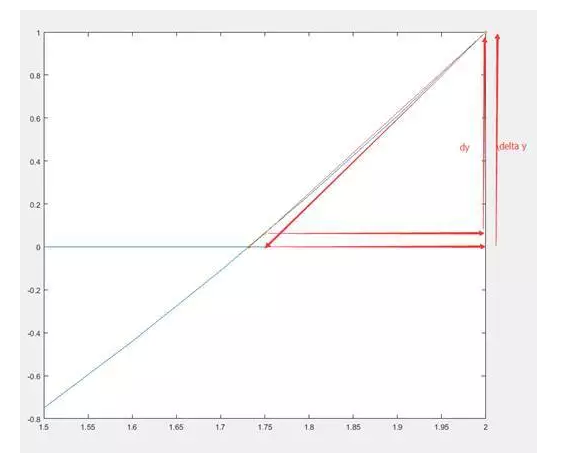

沒錯就是這么簡單。
這里順帶一提,對于不同的方程起始點的選擇也會影響迭代次數,如果有興趣的話可以讀一下 這篇文章 ,看一下神奇的0x5f375a86,2次迭代求解,這里讀兩次不讀二次^_^
那牛頓法和極值求解有關系?看起來牛頓法只能求零點啊? Naive~~,一階導零點不就是函數的極值或者駐點?

這個矩陣就是傳說中的Hessian矩陣,不是什么拼音的簡寫。

還是以上面的例子解,對就是只有兩個點求直線的那個,這次我們把目標函數1/2的加上。
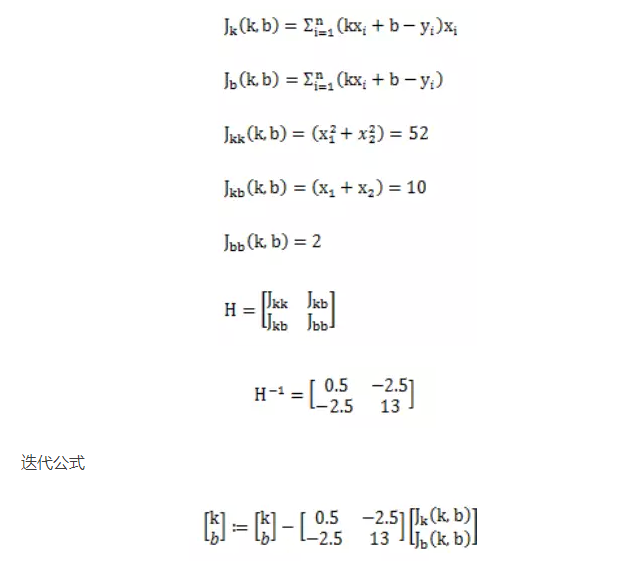
來看一下效果,看起來直接一步到位啊!!!所以牛頓法求解你們也應該知道多厲害了。
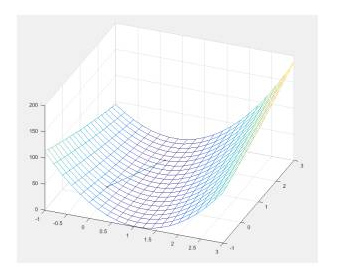
難道是我初始點選的就比較接近答案?換一個大一點的(100,100),依然非常快!
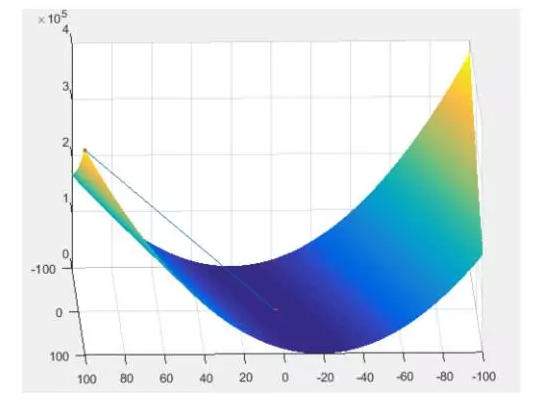
這么快的原因,可能跟方程有關,換了其他方程也許就不這樣了。當然你讀到這里也許會迫不及待的去找些自己想分析的數據,計算些參數,如果數據量少,幾百個,沒問題,幾萬個,還撐得住,要是直接從統計局或者人口普查中進行分析的話,算一個
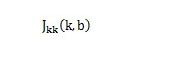
可能都很慢,而且數超大。
簡單的解決辦法,有一種叫做批迭代的方法,不管是在梯度計算極值還是在牛頓計算極值上都是可行的,就是假設失去大部分點對準確度沒有太大的影響,比如說3個在一條直線上的點,去掉一個也沒什么關系,最后反正還是會擬合成同一個參數。批迭代就是在眾多的點中隨機抽取一些,進行迭代計算,再隨機抽取一些再進行迭代。迭代的路徑可能不完美,但是最終還是會找到我們想要的答案。
歡迎加入本站公開興趣群商業智能與數據分析群
興趣范圍包括各種讓數據產生價值的辦法,實際應用案例分享與討論,分析工具,ETL工具,數據倉庫,數據挖掘工具,報表系統等全方位知識
QQ群:81035754
文章版權歸作者所有,未經允許請勿轉載,若此文章存在違規行為,您可以聯系管理員刪除。
轉載請注明本文地址:http://specialneedsforspecialkids.com/yun/4394.html
摘要:人工智能概述簡史應用領域安防實時從視頻中檢測出行人和車輛。通過多張醫療影像重建出人體內器官的三維模型,幫助醫生設計手術,確保手術為我們每個人提供康建議和疾病風險預警,從而讓我們生活得更加健康。 showImg(https://segmentfault.com/img/remote/1460000015971504); 0 引言 本文是《人工智能基礎(高中版)》的讀書筆記,這本書的配圖非...
摘要:人工智能概述簡史應用領域安防實時從視頻中檢測出行人和車輛。通過多張醫療影像重建出人體內器官的三維模型,幫助醫生設計手術,確保手術為我們每個人提供康建議和疾病風險預警,從而讓我們生活得更加健康。 showImg(https://segmentfault.com/img/remote/1460000015971504); 0 引言 本文是《人工智能基礎(高中版)》的讀書筆記,這本書的配圖非...
摘要:與此類似,理所當然的,我們程序員也會有自己的圣經。這便是程序員的圣經三個原則我認為做為一個程序員,最神圣的就是三個原則,它幾乎能完整無誤的定義做為一個程序員應該如何去編碼。 ...
閱讀 1960·2021-09-30 09:46
閱讀 1371·2019-08-30 15:43
閱讀 1130·2019-08-29 13:28
閱讀 1931·2019-08-29 11:24
閱讀 1690·2019-08-26 13:22
閱讀 3935·2019-08-26 12:01
閱讀 1826·2019-08-26 11:33
閱讀 3249·2019-08-23 15:34